具SR性质的基本双圈图
2010-11-26周后卿张于娟
周后卿,张于娟
(1.湖南邵阳学院数学系,中国 邵阳 422000;2.湖南师范大学数学与计算机科学学院,中国 长沙 410081)
设G为n阶简单图,其顶点集为V(G)={v1,v2,…,vn},G的邻接矩阵记为A(G),由于A(G)是实对称矩阵,则所有的特征值也是实数,A(G)的特征值也称为G的谱.若A(G)是奇异的(或非奇异的),则图G称为奇异的(或非奇异的).定义与记号见参考文献[1].
若图G存在一生成森林使得每一分支是仅2个点的路,则称G具有完美匹配.一般地,1个图可能存在不止1个完美匹配,而若树存在完美匹配,则完美匹配是唯一的,且此时树是非奇异的.容易看出,具唯一完美匹配的图是非奇异的.单圈图和双圈图的结构决定了邻接矩阵的奇异性,文[2]刻画了单圈图的邻接矩阵的奇异性与非奇异性分类.文[3~5]研究了双圈图的邻接矩阵的奇异性与非奇异性的分类.
本文作者考虑的是基本双圈图,即不含悬挂点的连通双圈图,它共有3种不同的类型(见图1):
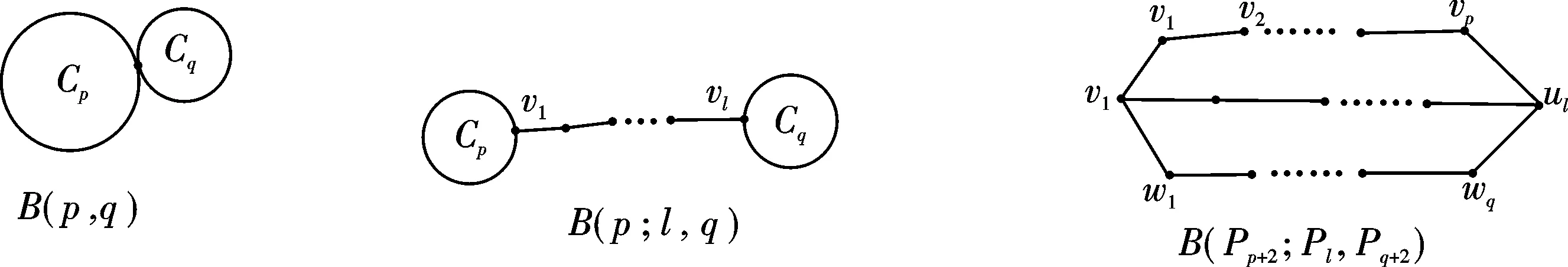
图1 基本双圈图
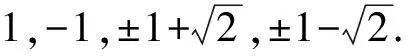
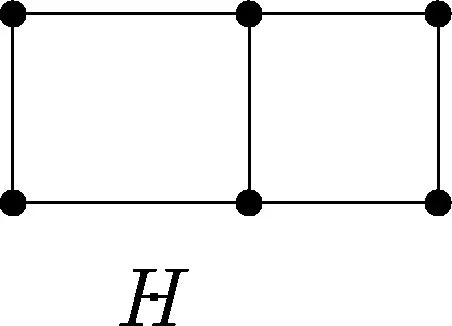
图2 图H
对任一图G,若S为G的一个点集或边集,则G-S表示由G删去所有S的元素得到的图.G的Sach子图L是其连通分支为边和圈的子图,当L的顶点集与G相同时,称L为G的生成Sach子图.G的k-匹配是指k条不相交的边的并,若e1,e2,…,ek为k-匹配M中的边,记作M={e1,e2,…,ek}.若2k为G的顶点数,则G的k-匹配为G的一个完美匹配,记m0(G)为G的完美匹配数.
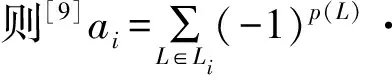
1 主要结果和证明
本节利用图具有SR性质的必要条件出发来研究基本双圈图的SR性质,得出只有图H具有SR性质,而其他图都不具有SR性质.
引理1[10]设G为n阶具有SR性质的图,邻接矩阵A(G)的特征多项式为P(G;x)=a0xn+a1xn-1+…+an,则|ai(G)|=|an-i(G)|,其中i=0,1,…,n.
从上可知,若某图G的特征多项式P(G;x)中有|ai(G)|≠|an-i(G)|,则G不具有SR性质.
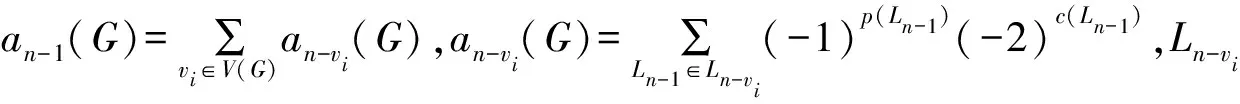
引理2设G为n阶基本双圈图且G=B(p,q)(p≥q≥3),两基圈分别为Cp,Cq,则G不具SR性质.
证用反证法,假设G具有SR性质,则|an(G)|=1,由于
an(G)=±(m0(G)±2m0(G-Cp)±2m0(G-Cq)),
(1)
1)若G有完美匹配,则n为偶数,此时m0(G)=2,由式(1)得an(G)=0(mod 2)与|an(G)|=1矛盾,所以此类图不具有SR性质;
2)若G没有完美匹配,此时m0(G)=0,由式(1)得an(G)=0(mod 2)与|an(G)|=1矛盾,所以此类图不具有SR性质.
综上,基本双圈图G=B(p,q)(p≥q≥3)不具有SR性质.
引理3设G为n阶基本双圈图且G=B(p,l,q),p≥q≥3,l≥2,两基圈分别为Cp,Cq,则G不具有SR性质.
证由于n阶基本双圈图G=B(p,l,q)中,
an(G)=±(m0(G))±2m0(G-Cp)±2m0(G-Cq)±4m0(G-Cp-Cq),
(2)
且p+q+l-2=n,假设G具有SR性质,必有|an(G)|=1.
1)若G有完美匹配,则n为偶数,对l分情况讨论:
(1)当l=1(mod 2),则p+q=1(mod 2),此时m0(G)=2,由式(2)得an(G)=0(mod 2)与|an(G)|=1矛盾,所以G不具SR性质.
(2)当l=0(mod 2),只能p=0(mod 2),q=0(mod 2),或p=1(mod 2),q=1(mod 2):①p=0(mod 2),q=0(mod 2),此时m0(G)=4代入式(2)得an(G)=0(mod 2)与|an(G)|=1矛盾,则G不具SR性质;②p=1(mod 2),q=1(mod 2),此时m0(G)=1,m0(G-Cp)=0,m0(G-Cq)=0,m0(G-Cp-Cq)=1,代入式(2)得an(G)=±3或±5,矛盾,则G不具SR性质.
2)若G没有完美匹配,则m0(G)=0,由式(2)得an(G)=0(mod 2),与|an(G)|=1矛盾,则G不具SR性质.
综上,基本双圈图G=B(p,l,q)不具SR性质.
引理4设G=B(Pp+2,Pl,Pq+2)(l≥2,p≥q≥1)为n阶基本双圈图且|an(G)|=1,则p,q,l必为下列6种情形之一:(1)l=0(mod 4),p=0(mod 4),q=0(mod 4);(2)l=0(mod 4),p=0(mod 4),q=2(mod 4);(3)l=0(mod 4),p=2(mod 4),q=0(mod 4);(4)l=2(mod 4);p=0(mod 4),q=2(mod 4);(5)l=2(mod 4),p=2(mod 4),q=0(mod 4);(6)l=2(mod 4),p=2(mod 4),q=2(mod 4).
证设n阶基本双圈图G=B(Pp+2,Pl,Pq+2)满足|an(G)|=1.由
an(G)=±(m0(G)±2m0(G-Γ1)±2m0(G-Γ2)±2m0(G-Γ))
(3)
知m0(G)≠0.故G有完美匹配,从而n为偶数.对p,q,l的取值分类讨论:
1)l=1(mod 2)时,必有p+q=1(mod 2),此时,m0(G)=2,代入式(3)得an=0(mod 2);
2)l=0(mod 2)时,必有p+q=0(mod 2):
(1)当p=1(mod 2),q=1(mod 2)时,m0(G)=2,代入式(3)得an=0(mod 2);
(2)当p=0(mod 2),q=0(mod 2)时,m0(G)=3,m0(G-Γ1)=1,m0(G-Γ2)=1,m0(G-Γ)=1,代入式(3)得an=±(3±2±2±2),分下列情况:
情形①:l=0(mod 4),p=2(mod 4),q=2(mod 4),an=+(3+2+2+2)=9;
情形②:l=2(mod 4),p=0(mod 4),q=0(mod 4),an=-(3+2+2+2)=-9;
情形③:l=0(mod 4),p=0(mod 4),q=0(mod 4),an=+(3-2-2+2)=1;
情形④:l=0(mod 4),p=0(mod 4),q=2(mod 4),an=-(3-2+2-2)=-1;
情形⑤:l=0(mod 4),p=2(mod 4),q=0(mod 4),an=-(3+2-2-2)=-1;
情形⑥:l=2(mod 4),p=0(mod 4),q=2(mod 4),an=+(3-2+2-2)=1;
情形⑦:l=2(mod 4),p=0(mod 4),q=2(mod 4),an=+(3+2-2-2)=1;
情形⑧:l=2(mod 4),p=2(mod 4),q=2(mod 4),an=-(3-2-2+2)=-1.
综上,得证.
引理5设G为n阶基本双圈图且G=B(Pp+2,Pl,Pq+2),l=0(mod 2),p=0(mod 2),q=0(mod 2),则
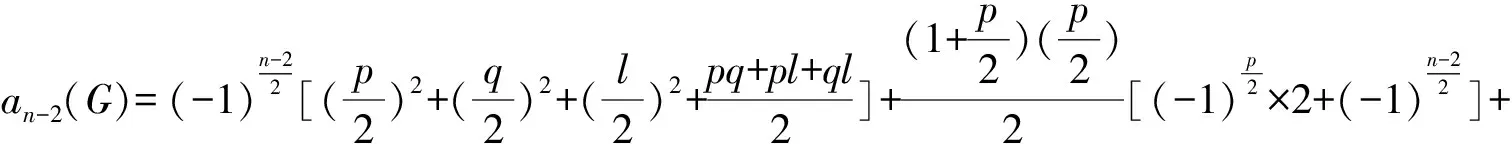
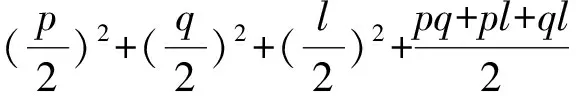
(4)
若为3),则是去掉路Pp+2上的两点(不包括端点)后有生成Sach子图可能含圈Γ2,此时
(5)
若为4),则是去掉公共路Pl上的两点(包括端点)后有生成Sach子图可能含圈Γ,此时
(6)
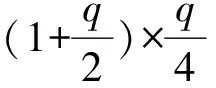
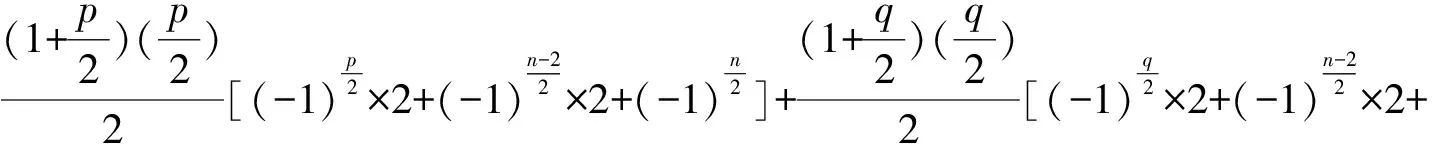
整理后即得结论.
定理1设G为n阶基本双圈图且G=B(Pp+2,Pl,Pq+2),则只有当n=6,p=q=l=2时,此时图G=B(P4,P2,P4)有SR性质,而其他图都不具SR性质.
证由引理4知|an(G)|=1的情形,而an-1(G)=0,现考虑an-2(G),由引理1知,G若不满足|an-2(G)|=|a2(G)|,则G一定不具SR性质.由于p+q+l=n,下面分情况讨论:
(1)l=0(mod 4),p=0(mod 4),q=0(mod 4),不妨设l=2k0,p=2k1,q=2k2(k0,k1,k2均为偶数),由引理5知
|a2(G)|=n+1=p+q+l+1=2k1+2k2+2k0+1,
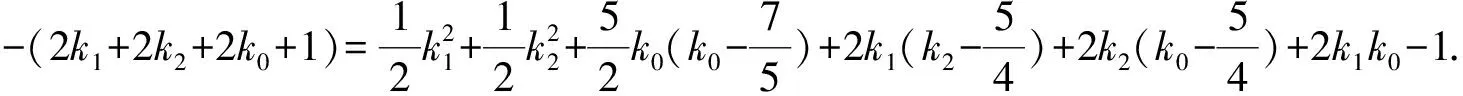
因为k0≥2,k1≥2,k2≥2,则|an-2(G)|-|a2(G)|>0,与图G具有SR性质的必要条件|an-2(G)|=|a2(G)|矛盾,所以此类图不具SR性质.
(2)l=0(mod 4),p=0(mod 4),q=2(mod 4);(3)l=0(mod 4),p=2(mod 4),q=0(mod 4);(4)l=2(mod 4),p=0(mod 4),q=2(mod 4);(5)l=2(mod 4),p=2(mod 4),q=0(mod 4),利用(1)的方法,可得|an-2(G)|-|a2(G)|>0.
(6)l=2(mod 4),p=2(mod 4),q=2(mod 4),不妨设l=2k0,p=2k1,q=2k2(k1,k0,k2均为奇数),由引理3知
|a2(G)|=n+1=p+q+l+1=2k1+2k2+2k0+1,
因为k0≥1,k1≥1,k2≥1,则|an-2(G)|-|a2(G)|≥0,等号成立当且仅当k1=k2=k0=1,即p=q=l=2.从而G为图H.
参考文献:
[1] HARARY F. Graph theory[M]. Addition-Wesley, 1969.
[2] 扈生彪.单圈图的邻接矩阵的分类及其最大行列式[J].数学研究,2003,36(1):102-104.
[3] 何梅芝.恰有一公共点的双圈图的邻接矩阵的奇异性[J].南华大学学报:自然科学版,2006,20(1):40-43.
[4] 兀静.n阶双圈图的邻接谱矩阵[J].海南师范学院学报:自然科学版,2006,19(4):289-300.
[5] 谢小花,陈宝兴,陈 宇.有交双圈图邻接矩阵的奇异性[J].漳州师范学院学报:自然科学版,2007,2:7-10.
[6] BARIK S, NEUMANN M, PATI S. On nonsingular trees and a reciprocal eigenvalue property[J].Linear and Multilinear Algebra, 2006,54: 453-465.
[7] FRUCHT R, HARARY F. On the corona of two graphs[J].Aequationes Math,1970,4:322-325.
[8] BARIK S, NATH M, PATI S,etal. Unicyclic graphs with the strong reciprocal eigenvalue property[J]. Electronic Journal of Linear Algebra, 2008,17:139-153.
[9] CVETKOVIC D M, DOOB M, SACHS H. Spectra of graphs[M]. New York:Academic Press,1979.
[10] BARIK S, PATI S, SARMA B K.The spectrum of the corona of two graphs[J]. SIAM J Discrete Math, 2007,21:47-56.
