求解P*(τ)阵线性互补问题的宽邻域路径跟踪算法

张莉，张涛

(1.四川省高等学校 数值仿真重点实验室，四川 内江 641112;2.内江师范学院 数学与信息科学学院，四川 内江 641112)

线性互补问题是规划论中的重要问题之一，线性互补问题从20世纪60年代提出到现在，已经出现了很多优秀的算法．总体上可以分为两类：一类是直接法，如Lemke算法，Cottle-Danting法；另一类是迭代法，如Mangrian法．到1984年,Karmarkar[1-2]提出内点算法以后，出现了很多求解线性互补问题的内点算法.文献[3]定理3.3.7证明了线性互补问题的解是存在唯一的，文献[4]给出求解一类非单调线性互补问题的内点算法的一般框架，文献[5]给出求解一类非单调线性互补问题的一种势能函数约减法，文献[6]给出(P-矩阵)线性互补问题的一阶窄邻域路径跟踪算法，文献[7]给出了(P-矩阵)线性互补问题的一阶宽邻域路径跟踪算法，并讨论了计算复杂性．然而，对于p*(τ)阵线性互补问题的内点算法研究甚少，本文在文献[7]的基础上，克服了p*(τ)阵线性互补问题关键性的困难，提出了一种宽邻域路径跟踪算法，讨论了计算复杂性，并给出了数值实验.

线性互补问题的一般形式是：求(x,z)∈Rn×Rn，使得：

z=Mx+b,(x,z)≥0,xTz=0

(1)

其中M∈Rn×n,b∈Rn.记

W=(x,z)|z=Mx+b,(x,z)>0，C=(x,z)∈W|Xz=μe,μ>0，

N2(β)=(x,z)∈W‖Xz-μe‖≤μβ，N∞(β)=(x,z)∈W‖Xz-μe‖∞≤μβ，

其中nμ=xTz,β∈(0,1)是适当确定的常数．称W为问题(1)的严格可行内点集，称C为问题(1)的中心路径，N2(β)和N∞(β)分别为包含中心路径C的一个2-范数的窄邻域和∞-范数的宽邻域．本文假设W非空．约定当英文小写字母例如x表示向量时，对应的大写字表示对角矩阵X=diag(x),e=(1,…,1)T，‖·‖和‖·‖∞分别表示2-范数和∞-范数．

本文假设M为P*(τ)阵[8]．所谓P*(τ)阵即存在实数τ≥0，使得对∀x∈Rn，有

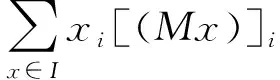
其中I=i|1≤i≤n,xi[(Mx)]i≥0．

1 算法描述

求解问题(1)的路径跟踪算法的基本思想是通过产生中心路径的一个邻域中的迭代点列逼近问题的解．对问题(1)的近似解(x,z)∈N∞(β)，在当前迭代点求解下面的方程组得到迭代方向(Δx,Δz)．

Δz-MΔx=0

(2)

ZΔx+XΔz=γμe-Xz

(3)

其中γ,β是适当选取的常数：γ∈(0,2/3),β∈(0,1)，且γ≤2(1-β)

(4)

记

x(θ)=x+θΔx,z(θ)=z+θΔz,nμ(θ)=x(θ)Tz(θ)

(5)

然后适当选取步长θ*，并取x+=x(θ*)=x+θ*Δx,z+=z(θ*)=z+θ*Δz，作为新的近似解．

下面给出算法步骤：

①选取初始点(x0,z0)∈N∞(β)，按(4)式选取常数β,γ，允许误差ε，置k=0;

②若(xk)Tzk≤ε，则停止，否则转步骤③;

③置(x,z)=(xk,zk)，解方程组(2)，(3)得迭代方向(Δx,Δz);

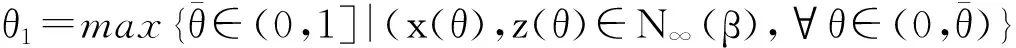
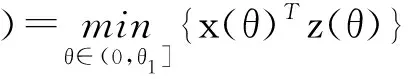
⑤置(xk+1,zk+1)=(xk,zk)+(θ*Δx,θ*Δz),k=k+1,转步骤②.

2 算法的收敛性及迭代复杂性分析

利用(5)和(3)式，直接计算可以得到下面两个重要关系式

μ(θ)=(1-θ)μ+θγμ+θ2ΔxTΔz/n

(6)

X(θ)z(θ)-μ(θ)e=(1-θ)(Xz-μe)+θ2ΔXΔz-θ2ΔxTΔze/n

(7)

这里着重指出，对于线性规划，ΔxTΔz=0；对于凸二次规划及单调线性互补问题，ΔxTΔz≥0；但是对于P*(τ)阵非单调线性互补问题，正如下面的引理1指出的那样，ΔxTΔz≥某一个负数．从而在收敛性分析中带来一系列的困难，无论是窄邻域还是宽邻域，解决这些困难都成为解决问题(1)的关键所在．

引理1 设(x,z)∈N∞(β),(Δx,Δz)是方程组(2)，(3)的解，则有

① 2ΔxTΔz≥-τ‖r‖2

(8)

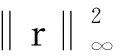
(9)

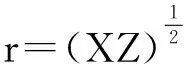
引理1的证明用类似于文献[9]中引理1的证明方法，易证(8)式.

(10)

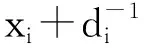
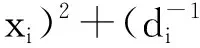
(11)

(11)式i=1,2,…,n.两边累加后，得

‖DΔx‖2+‖D-1Δz‖2+2ΔxTΔz=‖r‖2

(12)

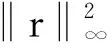
这就证明了(9)式．

引理2 设(x,z)∈N∞(β),(Δx,Δz)是方程组(2)，(3)的解，β,γ按(4)式取值，则有

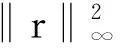
(13)

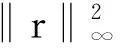
(14)

引理2的证明由(x,z)∈N∞(β)，有0≤(1-β)μ≤xizi≤(1+β)μ,i=1,2,…,n.

再由γ≤2(1-β)，有

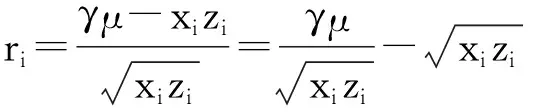
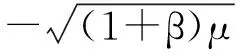
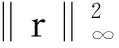
再由(9)和(13)式，有

‖ΔXΔz‖≤‖DΔXD-1Δz‖≤‖DΔX‖‖D-1Δz‖=‖DΔx‖∞‖D-1Δz‖≤

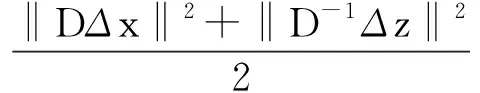
即(14)式成立.

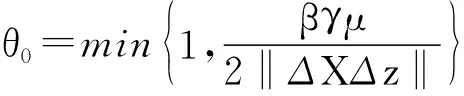
①0<[1-(1-γ/2)θ]μ≤μ(θ)≤[1-(1-3γ/2)θ]μ

(15)

②θ‖ΔXΔz-ΔxTΔze/n‖∞≤βγμ/2

(16)

引理3的证明∀θ∈(0,θ0]，有θ‖ΔXΔz‖≤θ0‖ΔXΔz‖≤βγμ/2，注意

|ΔxTΔz|/n≤‖ΔXΔz‖∞≤‖ΔXΔz‖，

有

θ2ΔxTΔz/n≥-θ2‖ΔXΔz‖≥-θβγμ/2≥-θγμ/2，θ2ΔxTΔz/n≤θ2‖ΔXΔz‖≤θβγμ/2≤θγμ/2,

将上述2式分别代入(6)式得(15)式．

由于‖ΔXΔz-ΔxTΔze/n‖2=‖ΔXΔz‖2-2(ΔxTΔz)2/n+(ΔxTΔz)2/n≤‖ΔXΔz‖2,

因此θ‖ΔXΔz-ΔxTΔze/n‖∞≤θ‖ΔXΔz‖≤βγμ/2.

引理4 在引理3的条件下，∀θ∈(0,θ0]，有(x(θ),z(θ))∈N∞(β)，于是算法步骤④中的θ1≥θ0.

引理4的证明1)∀θ∈(0,θ0]，由(7)、(16)、(15)式，注意(x,z)∈N∞(β)，有

‖X(θ)z(θ)-μ(θ)e‖∞≤(1-θ)‖Xz-μe‖∞+θ2‖ΔXΔz-ΔxTΔze/n‖∞≤

(1-θ)βμ+θβγμ/2=[1-(1-γ/2)θ]μ·β≤μ(θ)β,

即

‖X(θ)z(θ)-μ(θ)e‖∞≤μ(θ)β.

2)由所证结论1)、(15)式及μ(θ)>0，得

∀θ∈(0,θ0]，有xi(θ)zi(θ)≥(1-β)μ(θ)>0,i=1,2,…,n

(17)

下面证明必有(x(θ),z(θ))>0.否则(注意(17)式)，∃i，∃θ2∈(0,θ0],使得xi(θ2)<0,zi(θ2)<0.

由xi(θ2)=xi+θ2Δxi<0,xi>0,θ2>0，知Δxi<0，故∃θ3∈(0,θ2],使得xi(θ3)=xi+θ3Δxi=0，这与(17)式矛盾.

3)容易知道，(x(θ),z(θ))满足z(θ)=Mx(θ)+b.因此最后得到(x(θ),z(θ))∈N∞(β)，于是由算法步骤④中的θ1的定义知，θ1≥θ0.

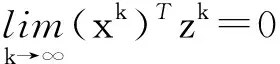
定理1的证明由(14)式，‖ΔXΔz‖≤(n+τ)μ，注意到βγ/2(n+τ)<1，因此在每次迭代中，有θ0=βγμ/2‖ΔXΔz‖≥βγ/2(n+τ).由算法步骤④中的θ*的定义及(15)式，有

(xk+1)Tzk+1=x(θ*)Tz(θ*)≤x(θ0)Tz(θ0)=nμ(θ0)k≤[1-(1-3γ/2)θ0]nμk≤

[1-((1-3γ/2)βγ)/2(n+τ)](xk)Tzk.

因此

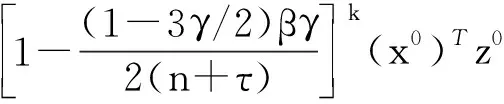
(18)

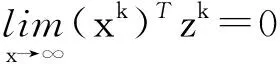
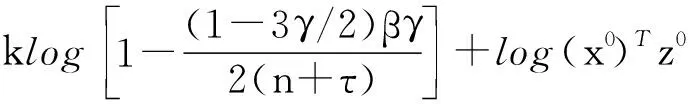
于是当k≥K时，有log(xk)Tzk≤logε，(xk)Tzk≤ε，即算法的迭代次数不超过K.

定理1表明，算法的迭代复杂性为O((n+τ)log((x0)Tz0ε-1))，与p*(τ)阵的参数τ有关．特别当τ=0时(即单调线性互补问题)，则迭代复杂性为O(nlog((x0)Tz0ε-1)).

3 数值实验

本节讨论本文中给出的算法用Matlab语言编程对几个标准的测试问题进行测试，并给出了实验结果，见表1和表2．

表1 Murty问题及Fathi问题的数值实验结果

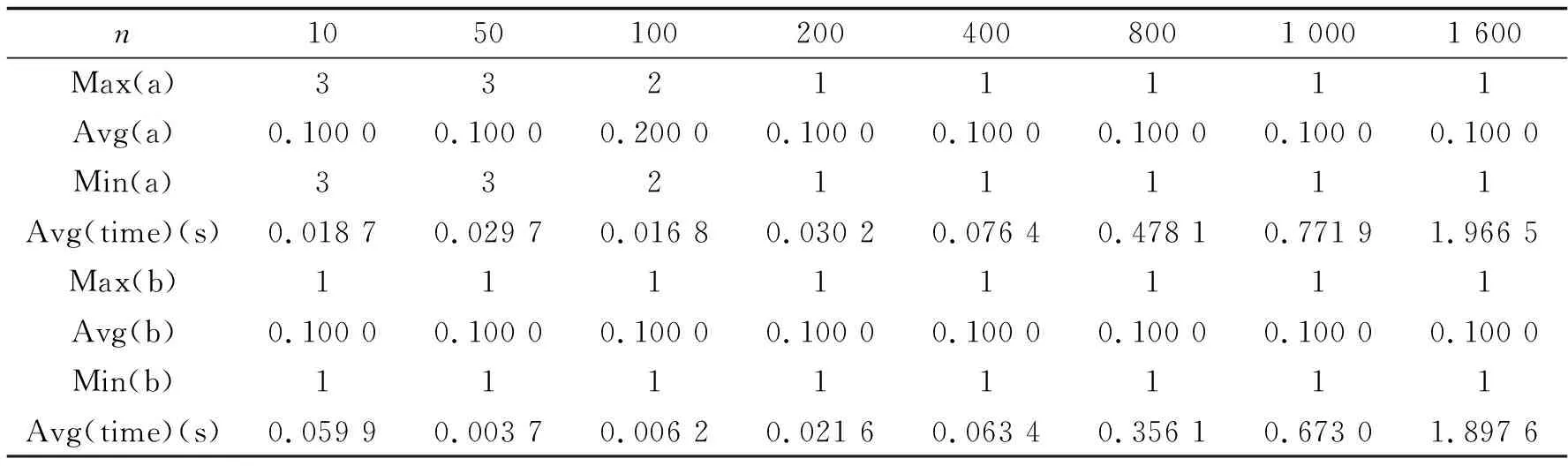
表2 随机产生的P-矩阵数值实验结果

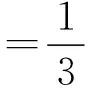
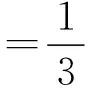
例3.3(产生随机的P-矩阵[10]) 由机器的随机数发生器产生伪随机数aij∈(-5,5),ηi∈(0.0,0.3),1≤i,j≤n,bij∈(-5,5),1≤i,j≤n,设A=(aij),B为由bij构造的反对称矩阵，取M=ATA+B+diag(η),(a)产生伪随机数qi∈(-500,500),1≤i≤n；(b)产生伪随机数qi∈(-500,0),1≤i≤n.

4 结束语

针对P*(τ)阵线性互补问题，提出了一种新的内点算法—宽邻域路径跟踪算法．该算法基于精典线性规划路径跟踪算法思想，把宽邻域路径跟踪算法推广到P*(τ)阵非单调线性互补问题，给出了算法的具体步骤，讨论了算法的迭代复杂性．由于P*(τ)阵线性互补问题没有现成的测试函数，自己构造一是比较困难，二是不便于与其它算法进行比较．因此，本文给出的数值实验实际上是P*(τ)阵线性互补问题的一个特殊问题——P-矩阵线性互补问题，从实验的结果可以看到效果比较理想，也可以预测到只要有P*(τ)阵线性互补问题的测试函数，效果也应该比较理想，并且有望推广到大规模计算问题上．

参考文献：

[1] Karmarlcar N.A new polynomial-time algorithm for linear programming[C].Proceedings of the 16th Annual ACM Symposium on the Theory of Computing,1984:302-311.

[2] Karmarlcar N.A new polynomial-time algorithm for linear programming[J].Combindtoricd,1984,4:373-395.

[3] Cottle R W, Pang J S,Stone R E.The linear complementary problems[M].Boston:Acedemic Press,1992.

[4] Kojima M,Megiddo N, Mizuno S.A general framework of continuation methods for complementary problems [J].Mathematics of Operations Research,1993,18(4): 945-963.

[5] Kojima M,Megiddo N,Ye Y.An interior-point potential reduction algorithms for the linear complementary problems[J].Mathematical Programming,1992,54(2):267-279.

[6] 何尚录，徐成贤.求解一类非单调线性互补问题的路径跟踪算法及其计算复杂性[J].计算数学，2001,23(3):299-306.

[7] 张莉，王浚岭，张明望.修正一类非单调线性互补问题的宽邻域路径跟踪算法[J].工程数学学报，2007，24(4):707-711.

[9] Mizuno S,Todd M J,Ye Y.On adaptive-step primal-dual interior-point algorithms for linear research[J].Mathematics of Operations Research,1993,18:964-981.

[10] Kanzow C. Some noniterior continuation methods for linear complementarity problem[J].SIAM J Matrix Anal,1996,17:851-868.