含高斯符号问题的解法探究
2010-11-23新星学校浙江苍南325800
● (新星学校 浙江苍南 325800)
含高斯符号问题的解法探究
●易永彪(新星学校 浙江苍南 325800)
在解决实际问题以及计算机的运算中,常常需要对一些数据进行取整运算,即把一些不是整数的实数去掉它的正纯小数部分,用不超过它的最大整数取而代之:设x是实数,不大于x的最大整数叫做x的整数部分,记作[x].

1 确定范围
要求某个数式的整数部分,可以先确定这个数式的取值范围,而且这样的范围越精确越好.
例1[x],[y],[z]分别表示不超过x,y,z的最大整数,若[x]=5,[y]=-3,[z]=-2,则[x-y+z]可以取值的个数是
( )
A.1 B.2 C.3 D.4
分析由x,y,z的范围,可确定x-y+z的取值范围.
由[x]=5,[y]=-3,[z]=-3,可得
5≤x<6,-3≤y<-2,-2≤z<-1,
因此
2<-y≤3,
于是
5 故[x-y+z]的值可以为5或6或7,选C. 分析可以先设法确定S的取值范围. 而 又 就是把取整问题转化为解某不等式的问题,可利用0≤{x}<1,[x]≤x<[x]+1. 例3用[x]表示不大于x的最大整数,则方程6x-3[x]+7=0的解是________或________. (2010年第21届希望杯初二数学竞赛第一试试题) 分析由6x-3[x]+7=0,可得 因为[x]≤x<[x]+1,所以 于是可化为不等式组 解得 因此 解得 分析利用性质x-1<[x]≤x,得 2x-1<[2x]≤2x,3x-1<[3x]≤3x, 因此 5x-2<[2x]+[3x]≤5x, 于是可化为不等式 解得 因而 这就是充分利用x=[x]+{x}的关系解题. 例5已知x,y,z满足 求x,y,z的值. 分析因为x=[x]+{x},由式(1)+式(2)+式(3)得 2(x+y+z)=0.6, 所以 x+y+z=0.3. (4) 式(4)-式(1),得 {y}+[z]=1.2, 于是 [z]=1,{y}=0.2. 式(4)-式(2),得 {x}+[y]=0.1, 于是 [y]=0,{x}=0.1. 式(4)-式(3),得 {z}+[x]=-1, 于是 [x]=-1,{z}=0. 从而 x=[x]+{x}=-0.9, y=[y]+{y}=0.2, z=[z]+{z}=1. 评注本题各式中同时出现了[x],{x},[y],{y},[z],{z},作整体考虑后发现,可以结合性质x=[x]+{x},采用迭加的方法,得到x+y+z=0.3.由此再各个突破得解. 解含高斯符号的数学竞赛题,关键是要把握好它的意义与核心性质:x=[x]+{x}.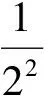




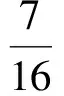
2 不等分析


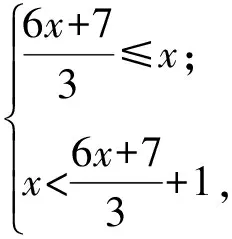
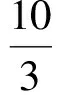
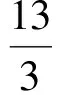


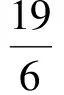
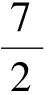
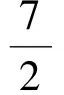


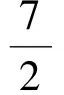

3 整体考虑