创新体现 创新架构 创新渗透——2010年数学高考“创新三步曲”赏析

● (湖州市第二中学 浙江湖州 313000)

近几年全国各地高考试题逐渐强调考查创新意识和应用意识，强调理论与实践相统一.一些新颖的试题背景、试题类型在近几年的试卷中从无到有、从零星到常见、从粗糙到精致，这些变化都体现了高考命题在有意识地将新课程的理念落实到高考试题中去，这其中就蕴含了“创新三步曲”.

一步曲：“数学探究”的创新体现

图1

数学探究是指学生围绕某个数学问题，自主探究、学习的过程.这个过程包括：观察、分析数学事实，提出有意义的数学问题，猜测、探求适当的数学结论或规律，给出解释或证明.高考重点考查高中数学的主干内容，从2010年各地高考试题来看，无论课标卷还是大纲卷，创新题明显增多，开放程度增强，突出研究性、探索性和实践性.

例1如图1所示，一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面，记t时刻五角星露出水面部分的图形面积为S(t)(S(0)=0)，则导函数y=S′(t)的图像大致为

( )

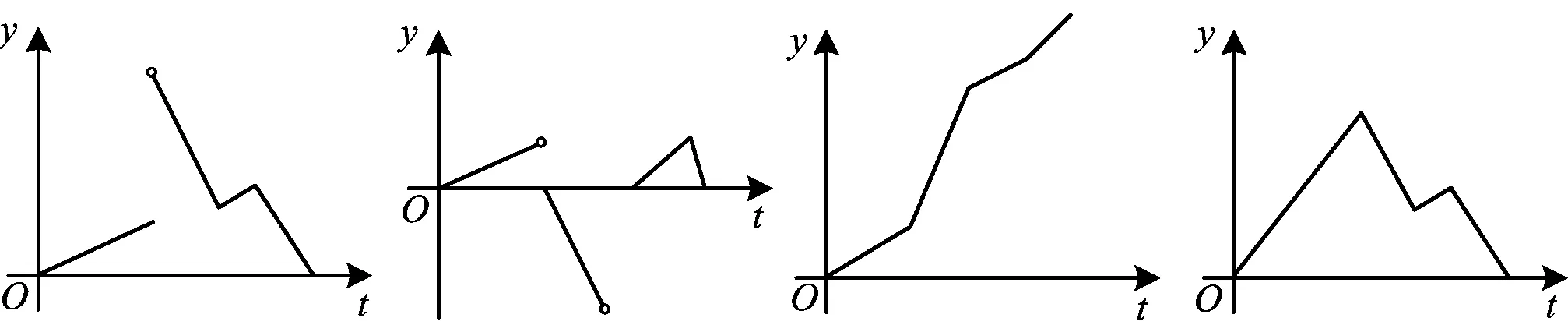
A. B. C. D.

(2010年江西省数学高考理科试题)

剖析本题主要考查函数图像、导数图像、导数的实际意义等知识，重点考查的是学生对数学的探究能力.此题的命题角度新颖、独特、创新，可使用“排除法”，答案为A.

例2若数列{an}满足：对任意的n∈N*，只有有限个正整数m使得am

(2010年湖南省数学高考理科试题)

剖析本题以数列为背景，通过创设适度开放，引导考生进行推理探索，此类题型可以说是新课标高考数学试题的一大亮点.答案为2，n2.

教学建议高考命题对数学思维能力作了新的阐释，它不但包含了原大纲提到的三大数学能力，即逻辑思维能力、空间想象能力与计算能力，而且将其扩展为直观感知、观察发现、归纳类比、空间想象、抽象概括、符号表示、运算求解、数据处理、演绎证明、反思与构建等思维能力.这不仅说明了我国对数学问题的研究在高考的促进下有了一定的发展，也为今后的教学指明了新的方向.

二步曲：“数学建模”的创新架构

“开展数学建模活动”是国际数学教育界推动数学教育改革的一个突破口.真正的数学建模活动需要学生付诸大量的时间，但作为在有限时间内考查学生数学能力的高考，设计的数学建模问题必须是“浓缩”的、“经典”的，便于学生寻找“模型”进行问题的分析与解决.它的特点是：对给出的实际问题进行了预先的简化与假设；问题的设计具有预设铺垫，难度层层递进，为学生搭建良好的“脚手架”，帮助学生能够在其能力范围内快速、有效地进入问题解决的核心.

(2010年江苏省数学高考试题)

剖析此类考题是比较常规的函数建模应用题.设剪成的小正三角形的边长为x，则

使用“换元法”或者“求导法”均可求得此函数的最小值.

图2

(1)求考察区域边界曲线的方程；

(2)设线段P1P2,P2P3是冰川的部分边界线(不考虑其他边界线)，当冰川融化时，边界线沿与其垂直的方向朝考察区域平行移动，第一年移动0.2 km,以后每年移动的距离为前一年的2倍，求冰川边界线移动到考察区域所需的最短时间.

(2010年湖南省数学高考理科试题)

剖析此题具备“大众化”的问题背景.因为参加高考的考生来自农村和城市各个阶层，所以拥有“大众化”背景的试题对考生来讲具有公平性.在考查数学建模的同时，将圆的方程、椭圆的定义与方程、直线与圆锥曲线的位置关系、等比数列求和等知识点巧妙地融为一体，要求考生能理解问题陈述的材料，并对所提供的信息资料进行归纳、整理和分类，将实际问题抽象为数学问题，从而建立数学模型；应用相关的数学方法解决问题并加以验证，且能用数学语言正确地表达和说明.

教学建议《新课标》倡导“发展数学应用意识和创新意识”.在数学教学中要对学生进行一定的数学建模训练，构造的问题要遵循“贴近生活、背景公平、控制难度”的原则，设计背景符合学生心理成长和学习生活实际、有一定时代气息、反映正确价值取向、科学严谨的问题，多角度地培养学生的数学应用意识和创新意识.

三步曲：“数学文化”的创新渗透

数学是人类文化的重要组成部分.将数学文化渗透于高考试题中是近几年高考的一个亮点，这样的问题走入高考，将引领学生关注数学的文化价值，形成对数学价值的全面认识，同时获得自身的和谐发展.

图3

例5如图3，一个小球从点M处投入，通过管道自上而下落到A或B或C处.已知小球从每个叉口落入左右2个管道的可能性是相等的.某商家按上述投球方式进行促销活动，若投入的小球落到A，B，C，则分别设为1，2，3等奖.

(1)已知获得1，2，3等奖的折扣率分别为50%，70%，90%．记随机变量ζ为获得k(k=1,2,3)等奖的折扣率，求随机变量ζ的分布列及期望Eζ；

(2)若有3人次(投入1球为1人次)参加促销活动，记随机变量η为获得1等奖或2等奖的人次，求P(η=2).

(2010年浙江省数学高考理科试题)

剖析往年浙江省的概率解答题均在“摸球问题”与“数字问题”之间“徘徊”，2010年的考题“一反常态”，令很多考生“措手不及”.其实此题源于数学史上著名的“高尔顿(钉)板”，在选修2-3“正态分布”的篇头就有介绍，因此此题是“源于课本、高于课程”的典范.

教学建议像这样渗透着“数学文化”的高考新题型给数学文化教育提供了很好的素材，可以引导学生探究“高尔顿板”与“二项分布”、“杨辉三角”的关系.在日常的教学中，可利用已有的高考题开展例题教学，也可自己开发编制此类新题，深刻挖掘此类问题中蕴含的数学思想和文化内涵，对学生开展数学文化教育.

结束语

高考试题对创新意识的考查，主要是要求考生不仅能理解一些概念、定义，掌握一些定理、公式，更重要的是能够应用这些知识和方法解决数学和现实生活中比较新颖的问题.数学教育的目的不只是让学生掌握一些知识，也不是把每个学生都培养成数学家，而是把数学作为材料和工具，通过数学的学习和训练，在知识和方法的应用中提高综合能力和基本素质，形成科学的世界观和方法论.因此，高考试题加强对创新意识的考查，其意义已超出了数学学习，对提高学习和工作能力、对今后的人生都有重要的意义.