2010年浙江省数学高考理科试题第18题解读

● (浬浦中学 浙江诸暨 311824)

对三角函数性质的考查一般以选择题、填空题的形式进行，且难度不大，三角函数解答题是近几年高考的必考题.在高考试题中，三角题多以解三角形且低档或中档题目为主，因而三角题成为考生在解答题中的主要得分点，要求做对、做全，尽量不失分.

(1)求sinC的值；

(2)当a=2,2sinA=sinC时，求b及c的长.

(2010年浙江省数学高考理科试题)

1 命题思路探寻

本题紧扣大纲与新课标要求：能运用公式(两角和与差及二倍角、同角关系式等公式)进行简单的恒等变换，掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题.本题的命题基本沿用前几年的风格,与2009年高考题相比难度略有下降.相对而言2010年的题目叙述简洁、清晰，使考生能以平稳的心态进行考试.

2 考生答题反馈

3 巧妙解法

常规解法：联系2C与C的关系应用二倍角公式计算sinC，结合三角形的边角问题应用正弦、余弦定理可解得b,c.在此,借助三角函数的定义进行求解.

根据圆的垂径定理,可知

同理可得,点N在第三象限(如图2)的情形(|MN|长度不变)，故

图1

图2

根据第(1)小题的图形可知：C有2种可能,故

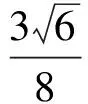
4 教学思考启示

作为新课程改革高考方案的第2年，总体上相对比较稳定，以基础知识、基本方法为命题出发点，顺应新课程改革的要求，让学生更多地参与到解题的探究过程中.因此在教学中应注意以下几点：

4.1 重视基础

发现学生概念错误，公式记忆不清楚，导致失分较多.因此在教学中,必须重视基础知识、基本的数学概念与公式,因而平时能通过应用公式来记忆显得尤为重要.

4.2 加强运算

由于现在的学生平时习惯于运用计算器，产生了一定的依赖性以至于削弱了自己的运算能力.在考试中丢三落四，出错率也高.在教学中,要求学生在平时的考试、练习时应尽量笔算，不要借助计算器，更不要养成眼高手低的习惯，导致在真正考试时手忙脚乱，甚至出现一些低级的运算错误.

4.3 形成网络

我们的教材是独立知识点教学，只在复习时将相关知识进行结合.知识块之间能形成一个网络，更有利于解答综合题.譬如解三角形问题常与向量、三角函数等结合，但解决三角形问题的工具仍为正(余)弦定理或面积公式，向量、三角函数作为一种转化问题的工具.

4.4 注重通法

加强重点问题的通性通法指导、保证解题的规范与严密.如三角函数、概率、立体几何、解析几何、函数与导数5个知识体系是近几年浙江省数学高考理科的常规解答题，应在平时强化此类问题的常规解法，形成一定的解题模式.解题的格式不够规范与不到位导致失分的学生比较多，在平时讲解中对易出错的相关环节应加强，使学生减少或避免这些无谓的失分.

总之,复习时应立足课本，抓好基础，重视数学思想方法的运用，强化应用意识的训练，提高分析问题、解决问题的能力.