2010年数学高考中有关函数与导数的试题赏析
2010-11-23分水高级中学浙江桐庐311519杭州市第十四中学浙江杭州310006
● (分水高级中学 浙江桐庐 311519) ● (杭州市第十四中学 浙江杭州 310006)
1 教学要求和考查要求
新课标清晰地阐述了函数导数的重要地位和广泛应用,并强调它的基础性和工具性,是中学数学的核心组成部分.近几年全国各地的数学高考试题在强调函数导数本质属性的同时也十分注重函数导数的工具性,解决的方法和手段也一改以往单一的手段,向既扎根定义又注重图像更依赖导数的方向迈进.这充分体现了函数概念、导数方法在中学数学中的核心地位,也更多地给予了学生一种思维的训练和人文的关怀.
(1)高考知识点:理解和掌握各种初等函数的图像和性质;函数的单调性与导数的关系;判别极大、极小值的方法;求函数最值的方法.
(2)教学注意点:必须在定义域内研究函数的图像、单调性、极值和最值;在求可导函数的极值时,应注意可导函数的零点是否为它的极值点.借助导数处理函数的单调性,进而研究不等关系,其关键在于构造函数.
2 命题特点和知识类型
2.1 借助函数图像的直观,深刻理解函数的性质
华罗庚先生说过“数以形而直观,形以数而入微”.近几年,高考中关于函数的考查更注重数与形的结合.

( )
A.(1,10) B.(5,6)
C.(10,12) D.(20,24)
(2010年宁夏数学高考理科试题)
分析1如图1,画出函数的草图.不妨设a>b>c,从图像中容易看出:
0 这样不难估计,abc∈(10,12). 分析2设f(a)=f(b)=f(c)=t,由图像可知 t∈(0,1),lga=-t,lgb=t,c=12-t, 于是 abc=10-t·10t·(12-2t)=12-2t. 又因为t∈(0,1),所以 abc∈(10,12). 图1 评注从题目的形式看这是一道常规试题,但从草图中能直接得到abc的取值范围还是出乎意料的.分析2其实是受到图像的启发,转化为函数最值问题,也是干净利落的. 例2已知定义域为(0,+∞)的函数f(x)满足:(1)对任意x∈(0,+∞),恒有f(2x)=2f(x)成立;(2)当x∈(1,2]时,f(x)=2-x. 给出如下结论:①对任意m∈Z,有f(2m)=0;②函数f(x)的值域为[0,+∞);③存在n∈Z,使得f(2n+1)=9;④“函数f(x)在区间(a,b)上单调递减”的充要条件是“存在k∈Z,使得(a,b)⊆(2k,2k+1)”.其中所有正确结论的序号是________. (2010年福建省数学高考理科试题) 图2 分析1如图2,画出满足条件的函数的草图. 观察图像,不难发现结论①,②,④正确. 分析2①因为 f(2m)=f(2·2m-1)=2f(2m-1)=…= 2m-1f(2)=0, 所以结论①正确. ②取x∈(2m,2m+1],则 得 于是 从而 f(x)∈[0,+∞), 即结论②正确. ③由上面的分析知,当2n+1∈(2n,2n+1]时, f(2n+1)=2n+1-(2n+1)=2n-1. 显然2n-1=9无整数根,因此结论③错误. ④根据前面的分析易知,结论④正确. 评注利用分析2直接计算也许不是很复杂,但解决函数问题的首选要素应该是函数的图像. 函数导数在中学数学中的核心地位随着新课标的推进而进一步加强,它既是研究函数的有利工具,又是对学生进行理性训练的良好素材,可借助导数研究函数的简易性和变易性的特点. (2010年湖北省数学高考理科试题) 分析观察待证式的结构,可先证不等式 成立,然后累加即得.因此只需证明 成立即可,即证函数 成立.因为 所以函数f(x)在[1,+∞)上单调递增,即 从而得到部分不等式 这也可能是命题人获得这个问题的最初方法. 例4已知函数f(x)=(a+1)lnx+ax2+1.设a<-1,若对任意的x1,x2∈(0,+∞),有|f(x1)-f(x2)|≥4|x1-x2|,求a的取值范围. (2010年辽宁省数学高考理科试题) 解得 函数导数是高中数学的核心概念,是全国各地高考的重点内容之一,函数与方程、数列、不等式的相互渗透和交叉一直是高考的热点和新的视点,可以说是常考常新.2010年全国数学高考试题与函数导数相关的部分亮点题呈现出如下特点: (1)考查函数图像与性质但不落俗套,给人耳目一新. ( ) A. B. C. D. (2010年江西省数学高考文科试题) (2)考查函数图像平移,采用纯数学语言表述,使问题变得新颖别致. ( ) A.4 B.6 C.8 D.10 (2010年浙江省数学高考理科试题) (3)考查问题贴近生活,就算是难题也乐于接受,特别是可以使学生感受到数学就在我们身边,从而增强学习数学的兴趣. 例7某学校要召开学生代表大会,规定各班每10个人推选1名代表,当各班人数除以10的余数大于6时再增选1名代表.那么,各班可推选代表人数y与该班人数x之间的函数关系用取整函数([x]表示不大于x的最大整数)可表示为 ( ) (2010年陕西省数学高考理科试题) 导数是研究函数图像、性质、证明不等式和解决一些实际问题的有力工具,在高考复习中要把握好3个层次:第1层次主要掌握基本初等函数图像性质以及导数的基本概念和常见实际背景,求导公式(c,sinx,cosx,ex,ax,xn,lnx,logax的导数)和求导法则;第2层次是掌握导数的简单应用,包括求函数的极值、求函数的单调区间、证明函数的增减性等;第3层次是能综合应用函数导数解决复杂问题,利用导数知识解决有关不等式和函数的单调性、方程根的分布等综合试题. 笔者建议如下: (1)无论何种教辅材料都不能作为教学的主要依据,复习时一定要回归教材.课本是试题的基本来源,大多数试题都是在课本的基础上组合、加工和发展的结果. (2)要把更多的注意力放在核心概念、基本数学思想方法上,不要片面追求所谓的新题和难题;要注重通性通法,不追求“特技”,……. (3)研究课程标准、考试大纲,领会高考样卷.高考命题以课程标准、考试大纲、考试说明(以及样卷)为指导,并结合高中数学的实际,这是高考命题的主要依据. (4)高等数学的基本思想、基本问题为高考题的命制提供背景,这既是高考考查潜能的需要,也是命题者学术背景使然. 因此,高考复习应依托考试大纲、考试说明,立足课本、课程标准,统领相关资源、历届高考试题、初高等数学的衔接地带和数学竞赛试题这几个方面.做到知己知彼,方能运筹于帷幄之中.



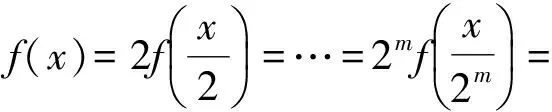
2 借助导数工具的简易,揭示函数的本质属性
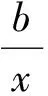
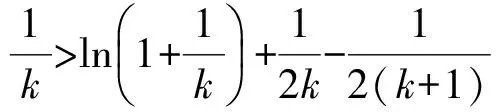





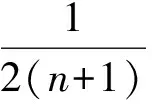
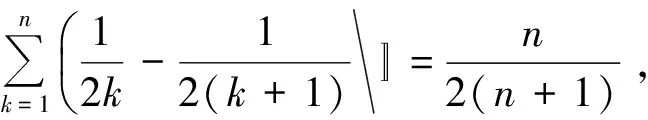
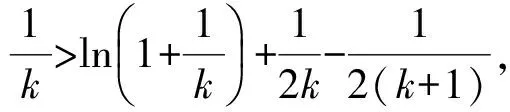
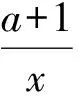
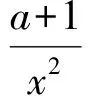


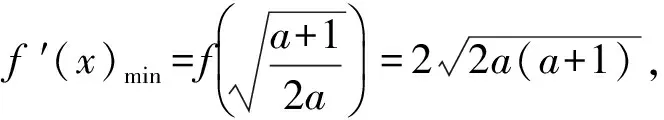

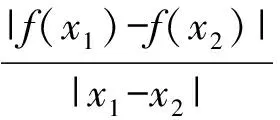
3 亮点扫描





4 复习建议
