2010年数学高考集合与常用逻辑用语试题评析
2010-11-23鲁迅中学浙江绍兴312000
● (鲁迅中学 浙江绍兴 312000)
在改革创新的大背景下,全国各地的高考试题立意鲜明,取材讲究,形式多样,难点分散,层次分明,具有创新意识,试卷充满活力、信度和效度,受到了社会各界广泛的关注和高度的重视;各地的高考试题在前几年保持相对稳定的基础上实现了3个转变,即主干知识更加突出、数学思想更加重要、思维能力更加强调,从而使试卷的难度有大幅度的提高.
课标版的“集合与常用逻辑用语”部分在沿袭前几年的考查知识和考查方式的基础上与大纲版的考查内容和方式上略有改变,考查的知识稳中有变,考查的方式变中求新.下面从4个方面评析全国各地高考“集合与常用逻辑用语”部分的试题.
1 教学要求对比分析
集合与常用逻辑用语既是高中数学的重要基础知识,又是高中数学的重要工具,可以说这部分内容是基础中的基础.
本专题新课程的教学要求主要有2个方面:
(1)集合方面:了解集合概念方面的含义,理解子集、交集、并集、补集的含义及集合间的包含、相等等关系,会求2个集合的交集、并集及给定子集的补集,能用韦恩图表达集合的关系与运算.
(2)常用逻辑用语:了解命题,逻辑联结词“或”、“且”、“非”及4种命题;理解充分、必要、充要条件的意义及全称量词、存在量词的含义;能正确地对含有一个量词的命题进行否定.
相对于大纲而言,新课程在集合与常用逻辑用语考查上主要是增加了“理解全称量词、存在量词的含义”等要求.
2 命题特点和知识类型
2.1 命题特点
1.1 分值比重
从2010年全国各地的高考试题分析可知,这块内容一般在高考中占5%~10%,其中新课程高考试题一般占的比重比大纲版的稍大,主要是增加了对常用逻辑用语的考查.
2.1.2 考查内容
集合的关系判定及集合间的运算、充要关系的判定、命题真假关系的判定等,其中新课程试题一般会考查新增的知识点“全称量词、存在量词”.
2.1.3 命题规律
(1)集合知识一般以一个选择题的形式出现,其中以集合知识为载体,集合与不等式、解析几何知识相结合是考查的重点,难度一般在中档偏下.
(2)对于逻辑用语的考查一般以一个选择题或一个填空题的形式出现,以集合、函数、数列、三角函数、不等式、立体几何中的线面关系为载体,考查充要关系或命题的真假判断,难度一般不大.
2.2 知识类型
2.2.1 集合概念与运算
(1)对集合基本概念的认识和理解水平,如集合的表示法、元素与集合的关系、集合与集合的关系、集合的运算等;
(2)以集合为工具考查集合语言和集合思想的应用水平,在考查集合知识的同时突出考查准确使用数学语言的能力及用数形结合、分类讨论思想解决问题的能力;
(3)以集合为载体考查对信息的收集、捕捉、加工的能力.
2.2.2 常用逻辑联结词
(1)命题的概念和命题的结构;
(2)逻辑联结词“或”、“且”、“非”的运用,2个量词的运用;
(3)命题的4种关系判断,一般会穿插在其他题目的考查中.
3 亮点扫描
3.1 集合单考显“纯”
集合与常用逻辑用语知识块中纯考查集合知识的也是2010年的一个亮点,这类试题几乎不与其他知识块结合,纯粹是运用集合知识考查集合知识,因而试题的难度也比较低,属容易题.
例1已知集合M={1,2,3},N={2,3,4},则
( )
A.M⊆NB.N⊆M
C.M∩N={2,3} D.M∪N={1,4}
(2010年湖南省数学高考理科试题)
解M∩N={1,2,3}∩{2,3,4}={2,3}.故选C.
点评本题主要考查集合的交集与子集的运算,给出的2个集合是有限的简单整数集的子集,考查理解和应用都较为轻松,属容易题.在高考试题中,类似的题目还有湖北省数学高考文科试题第1题等.
3.2 函数交汇显“综”
集合、常用逻辑用语与函数交汇尽显综合考查的目的,集合与函数的交汇可与函数的定义域、值域、对称轴、单调性、单调区间、周期等相结合考查函数与集合的知识与性质.这方面的试题难度属中下,有的试题也是考生的易错题.
例2函数f(x)=x2+mx+1的图像关于直线x=1对称的充要条件是
( )
A.m=-2 B.m=2
C.m=-1 D.m=1
(2010年四川省数学高考理科试题)
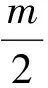
点评常用逻辑用语与函数的对称轴交汇,考查函数的图像、性质,既考查了函数的基本性质,也考查了常用逻辑用语的基本知识.在高考试题中,类似的题目还有福建省数学高考理科试题第15题.
3.3 向量交汇显“形”
平面向量也是数学运用中的一个重要工具,其重要性不言而喻,平面向量与集合、常用逻辑用语的交汇既体现了集合、常用逻辑用语的基本知识,也体现了数形结合中形的思想.
例3a,b为非零向量,“a⊥b”是“函数f(x)=(xa+b)·(xb-a)为一次函数”的
( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
(2010年北京市数学高考理科试题)
解由a⊥b,得a·b=0,则函数
f(x)=(xa+b)·(xb-a)=(b2-a2)x.
若|a|=|b|,则函数f(x)成为了常数函数,因此不一定成立;
反之,若f(x)=(xa+b)·(xb-a)为一次函数,则a·b=0,由a,b为非零向量,可知a⊥b.
综上所述,应选B.
点评常用逻辑用语与函数、平面向量交汇综合考查,既有考查平面向量中的“形”的一面,也具有考查函数图像和性质的功能,这类试题的设置有助于高考命题向“数学核心思想”迈进.
3.4 逻辑用语显“增”
常用逻辑用语中的全称量词和存在量词是新增的内容,因而也就成为了命题的一个亮点和热点,重视新增内容的考查也体现了命题者与教材编排者立意的统一.
例4下列命题中的假命题是
( )
A.∀x∈R,2x-1>0 B.∀x∈N*,(x-1)2>0
C.∃x∈R,lgx<1 D.∃x∈R,tanx=2
(2010年湖南省数学高考理科试题)
解对于选项B,当x=1时,(x-1)2=0.故选B.
点评对于常用逻辑用语的考查,主要是新增内容2个量词的考查,求解的关键是理解这2个量词的意义和用法.在高考试题中,类似的题目还有安徽省数学高考文科试题第11题.
3.5 信息交汇显“新”
信息试题是高考数学试题的创新源,信息题就是根据文字、图表、图形、图像等给出的数据信息,通过整理、加工、处理等手段去解决实际问题的一类题.在解答信息题时,首先要仔细观察阅读题目所提供的材料,从中捕捉有关信息(如数据间的关系与规律,图像的形状特点、变化趋势等),然后对这些信息进行加工处理,并联系相关数学知识,从而实现信息的转换,使问题顺利获解.
例5记实数X1,X2,…,Xn中的最大数为max{X1,X2,…,Xn},最小数为mix{X1,X2,…,Xn}.已知△ABC的3条边长为a,b,c(a≤b≤c),定义它的倾斜度为
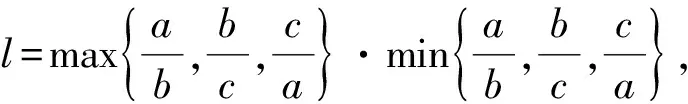
则“l=1”是“△ABC为等边三角形”的
( )
A.充分而不必要的条件
B.充要条件
C.必要而不充分的条件
D.既不充分也不必要的条件
(2010年湖北省数学高考文科试题)
解若△ABC为等边三角形,a=b=c,则
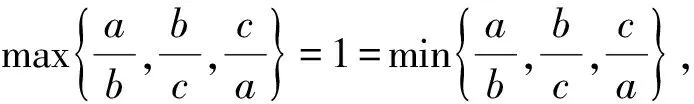
于是l=1;若△ABC为等腰三角形,如当a=2,b=2,c=3时,则
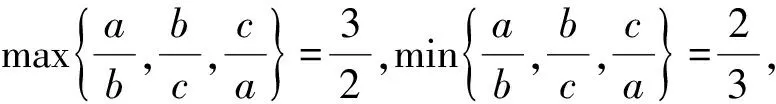
此时l=1仍成立,但△ABC不是等边三角形.故选B.
点评求解集合和常用逻辑用语中的信息问题,一要认真审题,二要结合集合、常用逻辑用语的意义;对于信息交汇问题,由于涉及到题目的知识背景新颖,对考生而言更具公平性,求解时需独立思考分析问题与解决问题.在高考试题中类似的题目还有福建省数学高考理科试题第15题.
4 复习建议
集合与常用逻辑用语的复习要注意把握2个知识点(集合和常用逻辑用语)、3个基本原则(基础知识理解、基本方法掌握、基本概念应用).
对于集合知识在复习中首先应深刻理解和把握集合、元素、子集、交集、并集、补集、命题、充要条件、逻辑联结词及2个量词的含义;其次是要抓好基本概念与运算的落实和对集合语言的识读理解能力;第三是要学会利用韦恩图、数轴、函数的图像等解题手段和策略,真正掌握数形结合的思想,学会用等价转化思想处理有关问题.
对于常用逻辑用语的复习,首先是要理解各种逻辑用语的含义、表示方法、用法及注意事项,理解命题结构及逻辑联结词“或”、“且”、“非”的含义,掌握4种命题的内在联系,熟练判断充要条件;其次是要注意对于常用逻辑用语客观题的训练,注意解答题中关键联结词的作用,并学会正确处理和化解.
