试题新颖开放 蕴含数学思想——2010年数学高考中有关三角函数试题的评析

● (海盐县教研室 浙江海盐 314300)

在原教学大纲和新课程标准中，三角函数都属于主干知识，是历年高考的基本要点之一.新课程将向量作为工具推导两角差的余弦公式，又将三角恒等变换独立成章，意在培养推理和运算能力，新课程删减了余切、正割、余割和已知三角函数值求角以及反三角符号等内容，也删除了用积化和差、和差化积、半角公式作复杂的恒等变形，避免了三角问题解决中过份的技巧性训练.2010年高考三角试题继续贯彻了新课程的上述要求.

1 命题特点和知识类型

1．1 三角化简或求值

三角函数的化简、求值是三角公式运用的重要方面，高考时或用一个公式，或需要几个三角公式的综合运用.

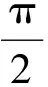
(2010年上海市数学高考文科试题)

分析本题的解决需要综合运用同角三角函数基本关系、两角和余弦公式、诱导公式等.

原式=lg(sinx+cosx)+lg(sinx+cosx)-

lg(sinx+cosx)2=0.

1.2 求三角函数的性质

通过三角恒等变形可将原三角函数化简为基本的正弦型y=Asin(ωx+φ)+k(或余弦、正切型)函数，然后求相关函数的性质.

(1)求函数f(x)的最大值；

(2)求函数f(x)的零点的集合.

(2010年湖南省数学高考理科试题)

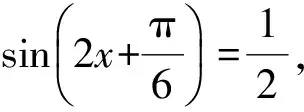
最后得到函数f(x)的零点的集合为

1.3 三角函数的图像

三角函数图像的考查一般涉及三角函数的图像变换和周期等性质特征.

( )

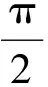
A．4 B．6 C．8 D．12

(2010年福建省数学高考文科试题)

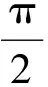
1.4 解三角形

三角形知识的考查或以正弦定理、余弦定理为工具，或综合三角恒等变换解决与三角形有关的问题.

(1)求sinC的值；

(2)当a=2,2sinA=sinC时,求b及c的长．

(2010年浙江省数学高考理科试题)

解答过程请参见本期第13页.

1.5 三角函数应用

应用三角函数特别是通过解三角形，可以解决测量等实际问题.

例5某兴趣小组测量电视塔AE的高度H(单位m)，如图1，垂直放置的标杆BC高度h=4 m，仰角∠ABE=α，∠ADE=β.

图1

(1)该小组已经测得一组α，β的值，tanα=1.24,tanβ=1.20,请据此算出H的值；

(2)该小组分析若干测得的数据后，发现适当调整标杆到电视塔的距离d(单位m)，使α与β之差较大，可以提高测量精确度，若电视塔实际高度为125 m，问d为多少时，α-β最大.

(2010年江苏省数学高考试题)

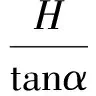
又由AD-AB=DB，得

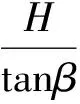
解得

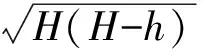
2 考查亮点扫描

2.1 试题形式新颖

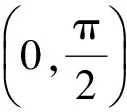
(2010年江苏省数学高考试题)

2.2 注重推理运算

主要体现在以三角问题为背景的探索规律等试题，例如：

例7观察下列等式：

①cos2a=2cos2a-1；

②cos4a=8cos4a-8cos2a+1;

③cos6a=32cos6a-48cos4a+18cos2a-1;

小学数学是学生学习的重要阶段，这一阶段将直接影响到学生今后的学习态度、学习习惯及学习能力。因此，小学数学教师应该重视学生的学习，引导学生学习和思考，帮助学生树立学习的信心，让学生在学习过程中感知学习的乐趣，不断进步，让学生在鼓励和激励中发现数学的价值，为今后的数学学习奠定基础，并使学生的学习能力、解决问题的能力能够得以体现和运用。

④cos8a=128cos8a-256cos6a+160cos4a-32cos2a+1;

⑤cos10a=mcos10a-1 280cos8a+1 120cos6a+ncos4a+pcos2a-1.

可以推测，m-n+p=________．

(2010年福建省数学高考文科试题)

分析因为 2=21,8=23,32=25,128=27,

所以

m=29=512；

观察可得

n=-400，p=50，

于是

m-n+p=962.

本题通过三角变换、类比推理等考查了考生的推理能力等.

2.3 解题形式开放

三角开放题中同样包含着问题解决的多种途径，例如：

( )

A. B.

C. D.

(2010年江西省数学高考文科试题)

2.4 蕴含数学思想

解决三角函数与其他函数、方程或不等式交汇的问题时，需要数形转换，或需要将函数与方程不等式进行转化.例如：

例9设函数f(x)=4sin(2x+1)-x，则在下列区间中函数f(x)不存在零点的是

( )

A．[-4,-2] B．[-2，0]

C．[0，2] D．[2，4]

(2010年浙江省数学高考理科试题)

分析将f(x)的零点转化为函数g(x)=4sin(2x+1)与h(x)=x的交点，数形结合可知应选A.本题是三角函数图像的平移与函数、方程的知识交汇题，突出了对转化思想和数形结合思想的考查.

2.5 公式推导回归教材

2010年的高考试题中出现了三角公式的证明和推导，例如：

例10(1)证明两角和的余弦公式Cα+β∶cos(α+β)=cosαcosβ-sinαsinβ；

(2)由Sα+β推导两角和的正弦公式Sα+β∶sin(α+β)=sinαcosβ-cosαsinβ.

(2010年四川省数学高考理科试题)

本题的考查源于教材，既有对两角和余弦公式推导证明的要求(向量法等)，又有通过诱导公式等方式对两角和、差余弦和正弦进行转换的要求.这样的考查体现了新课程对三角变换的推理要求.

3 复习建议

3.1 梳理知识,形成网络

三角函数作为一类特殊函数同样在定义基础上研究其图像和性质.一方面,诸多三角公式都有其适用针对性也有相互间的密切联系;另一方面,三角公式是三角恒等变换的工具,通过综合运用可以将一般三角函数变形化归为基本三角函数，从而求值、化简和研究其图像和性质.选择运用三角公式要注意观察角之间的关系，对一些公式还要会逆用和变形应用，譬如两角和差的正切公式、正余弦二倍角公式等的变形运用.

3.2 把握整体,渗透思想

三角问题解决中注意运用化归思想.求三角函数的值域、单调区间及判断其奇偶性和求周期等，主要是通过恒等变形将一般三角函数化归为基本三角函数类型.三角变形和转换过程中要注意等价思想.运用三角公式变形时,不少公式左右范围并不等价，而且这些条件往往是隐含的，又如运用三角图像或三角函数线研究性质时，常有自变量范围的限制，因此在问题解决过程中须注意前后的等价.三角函数线和三角函数图像是三角概念和性质的直观反映，它可以运用于求三角最值和有关三角方程根、单调等性质的研究，也可以运用于比较大小或不等式问题，它是数形结合的体现.

3.3 注重过程,提升能力

三角恒等变换是“只变其形不变其质”的，变换的目的在于揭示那些形式不同但实质相同的三角函数式的内在联系，通过基本公式的推导和简单应用能够培养推理和运算能力；通过探求和(差)角公式、倍角公式，以及运用这些公式推导和差化积、积化和差、半角公式等的过程，学生学习怎样预测变换目标、选择变换、设计变换途径等，从中学习运算、推理的基本思想，提升学生的运算能力和推理能力.