2010年数学高考解析几何试题评析

● (嘉兴市第一中学 浙江嘉兴 314001)

解析几何是高中数学的主干内容，在高考中占有重要的地位．由于“能力立意”是新课程高考的主要命题思想，因此在新课程高考中解析几何处于高考命题的主体位置．在当前《新课程标准》与《教学大纲》并存时期，研究新课程高考中解析几何命题的基本特征有助于提高现阶段高中数学教学的实效．

1 课程标准与教学大纲比较

随着新课程改革的推进，高考对解析几何的考查要求有很大的变化，其中对直线方程、圆的方程的考查要求有所加强，这点在2010年各省市的新课程数学高考试卷中得到了充分的体现．例如,湖南省数学高考文科试题第14题，山东省数学高考理科试题第16题，江苏省数学高考试题第9题等．在对圆锥曲线的考查上，新课程高考也有自己的特色，尤其是浙江省数学高考试题.从2009年及2010年的考试说明及高考试卷来看，解析几何的综合问题往往涉及直线与圆、椭圆及抛物线的位置关系，而对于传统意义上的直线与双曲线的位置关系则有了较大的淡化甚至回避．

解析几何的核心内容是用代数方法研究解决几何问题，它把数学的2个基本对象——形与数有机地联系起来.通过形与数的结合，使几何问题代数化，把几何要素及其关系用代数的语言加以描述;通过处理代数问题，分析代数结果的几何含义，最终解决几何问题．通过对解析几何的学习能够使学生进一步体会数形结合的思想.在这一点上，无论是新课程标准还是教学大纲，都是一致的．

2 2010年解析几何考情直播

2010年全国各地新课程的高考数学试卷(每套试题含文、理各1份，江苏省文、理合一)中以解析几何为主要考查内容的题目有59道(不含线性规划部分，有的是文、理姊妹题)，其中解答题25道，这说明每套试卷都有解析几何的解答题，而且解答题的题目在数学试卷中处于压轴位置．因此解析几何在每份试卷中所占分值较大，2010年浙江省数学高考理科试题中有1道选择题，1道填空题，1道解答题，分值为24分；文科卷中有1道选择题，1道解答题，分值为20分．其他省份的新课程数学试卷中涉及解析几何的题目一般也有20分以上，题量一般在2～5题．

从试题来看，有关解析几何的小题，其考查的重点在于解析几何的基础知识.例如浙江省数学高考理科试题第8,10题，北京市数学高考理科试题第13题，全国数学高考理科试题中第5,13题等都突出了对解析几何中直线与圆、圆锥曲线等内容中的基础知识的考查，譬如求直线方程、圆的方程、圆锥曲线的离心率等．有关解析几何的解答题中，例如浙江省数学高考理科试题第21题、文科试题第22题，广东省数学高考文科试题第21题，湖南省数学高考理科试题第19题等都重点考查了抛物线、椭圆、双曲线的相关内容，考查直线与圆锥曲线之间的关系问题(浙江省数学高考试题主要涉及直线与椭圆、直线与抛物线的位置关系).问题涉及函数、方程、不等式、三角、向量等有关知识的综合运用，综合考查学生的数形结合、等价转换、分类讨论、函数与方程、运动变化、逻辑推理等能力，考查学生对基本知识、基本方法、基本技能的理解、掌握和应用的情况．

3 亮点扫描

纵观2010年全国各地新课程数学高考试卷，其中许多解析几何试题设计新颖、构思巧妙、耐人寻味，令人赏心悦目，体现了“能力立意”的指导思想，凸显了数学试题的选拔功能．

亮点1试题设计背景新颖，考查学生的阅读理解能力.

图1

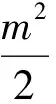
(1)当直线l过右焦点F2时，求直线l的方程.

(2)设直线l与椭圆C交于点A,B，△AF1F2，△BF1F2的重心分别为G,H．若原点O在以线段GH为直径的圆内，求实数m的取值范围．

(2010年浙江省数学高考理科试题)

亮点2试题设计关注交汇，考查综合运用能力.

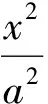
(1)求椭圆的方程；

(2010年天津市数学高考理科试题)

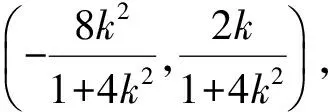
亮点3试题设计联系实际，考查学生用数学的能力.

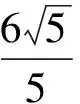
(1)求考察区域边界曲线的方程；

(2)如图2所示，设线段P1P2,P2P3是冰川的部分边界线(不考虑其他边界线)，当冰川融化时，边界线沿与其垂直的方向朝考察区域平行移动，第一年移动0.2 km,以后每年移动的距离为前一年的2倍，求冰川边界线移动到考察区域所需的最短时间．

(2010年湖南省数学高考理科试题)

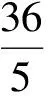
图2

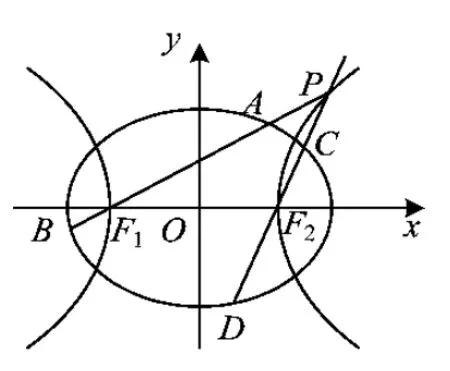
图3

亮点4试题设计重视探究，考查学生的探究能力.

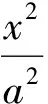
(1)求椭圆和双曲线的标准方程.

(2)设直线PF1,PF2的斜率分别为k1,k2，证明:k1·k2=1.

(3)是否存在常数λ，使得|AB|+|CD|=λ|AB|·|CD|恒成立？若存在，求λ的值；若不存在，请说明理由.

(2010年山东省数学高考理科试题)

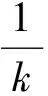
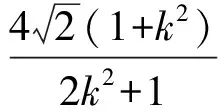
由题意得

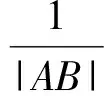
|AB|+|CD|=λ|AB|·|CD|

恒成立．第(3)小题的解决还需要有较强的运算能力，这也是解析几何的特点之一．培养学生的探究能力是新课程对学生的重点要求之一，因此在新课程的数学高考试卷中，通过解析几何问题来考查学生的探究能力显得比较普遍.例如山东省数学高考文科试题第22题、北京市数学高考理科试题第19题、陕西省数学高考理科试题第20题、安徽省数学高考理科试题第19题等都对学生的探究能力提出了较高的要求．

4 启示

(1)新课程高考中对解析几何的考查突出对解析几何基础知识与基本技能的考查，稳中有变，但变中又有“定”，因此在复习时要实行“以不变应万变”的策略.

(2)从2010年新课程高考数学试卷中可以看出解析几何问题中的“交汇”已突破解析几何的圈子，解析几何问题与向量、三角甚至数列、不等式内容相交汇已并不鲜见，因此在复习时应以整个高中数学知识为背景，全方位地复习，不能有丝毫的侥幸心理.

(3)从2010年新课程高考中的解析几何问题可以看出，在解析几何的学习中培养学生的思维能力固然重要，但是繁杂、冗长的推演、计算、变换过程也不可少，这是新课程高考对考生提出的能力要求之一.因此在复习中,既要重视对学生思维能力的培养，又要重视计算能力的训练，必须努力克服学生中轻视计算，容易出错的“眼高手低”的毛病．