题小意深 图穷意显
——2010年浙江省数学高考向量试题赏析及历史回顾
2010-11-23昌硕高级中学浙江安吉313300
● (昌硕高级中学 浙江安吉 313300)
从2004年浙江省自主命题以来,向量试题就呈现出鲜明的特点:具有极强的数学味和突出的几何背景;既可以考查向量的代数运算,也能通过对几何背景的透视,抓住向量本质,简化解题思路.但是在2009年的试题中却没能感受到这一点,正当我们以为向量的考查趋于平淡时,2010年浙江省数学高考理科试题第16题横空出世,让我们再次感受到了向量问题的奇特魅力.
例1已知平面向量α,β(α≠0,α≠β)满足|β|=1,且α与β-α的夹角为120°,则|α|的取值范围是________.
(2010年浙江省数学高考试题)
解法1设平面向量α,β的夹角为θ.由题意得
α·(β-α)=|α|·|β-α|cos120°.
因为
α·(β-α)=α·β-|α|2=
|α||β|cosθ-|α|2,
由|β|=1,得
|α|·|β-α|cos120°=|α|cosθ-|α|2,
所以
|β-α|=-2cosθ+2|α|,
即
|β-α|2=(-2cosθ+2|α|)2.
展开得
3|α|2-6|α|cosθ+4cos2θ-1=0,
解得
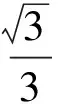
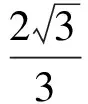
解法21=|β|2=β2=[α+(β-α)]2=
|α|2+|β-α|2-|α||β-α|,
即
|β-α|2-|α||β-α|+|α|2-1=0.
将|β-α|看成自变量,则
Δ=|α|2-4(|α|2-1)=-3|α|2+4≥0,
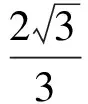

|α|2+|β-α|2-2|α|·|β-α|cos60°=|β|2=1.
以下同解法2.

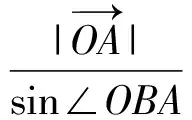
即
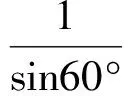
解得
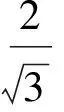
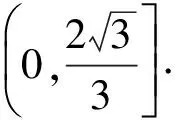

于是点B的轨迹方程为
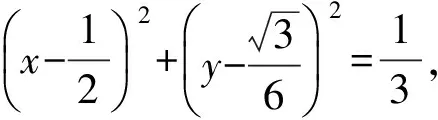
且点O,B均在圆上,从而
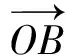
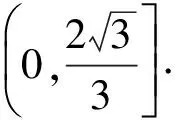

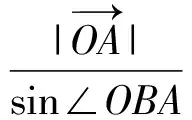
点B在以线段OA为弦,半径为R的圆上,因此
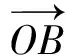
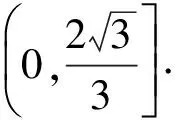
评析解法1利用向量数量积的2个公式进行恒等变换,构造出|α|与平面向量α,β的夹角θ的方程,是学生容易想到的纯代数方法,但其过程较繁,容易出错;解法2将β-α看成整体利用恒等变换,转化为函数问题处理,有一定的技巧性,总体上还是以代数的方法为主导;解法3和解法4将向量问题转化为三角问题,借助解三角形的方法来处理,有效地建立了向量与三角的联系,体现出向量的“回路”本质,也使问题变得清晰明了;解法5将向量问题转化为解析几何问题,通过求动点轨迹的方法处理,沟通了向量与解析几何的天然联系;解法6充分利用了点的性质,借助几何条件将向量、三角、平面几何有机地结合在一起.
再次回顾2004~2008年浙江省数学高考向量试题,可以发现其背后那一脉相承的几何背景.
1 初露端倪
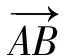
(2004年浙江省数学高考试题)
解由条件知,△ABC为直角三角形,且∠B=90°,因此

于是
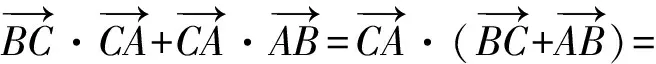

评析向量加入高中数学的“大家庭”不久,以直角三角形为背景构造的试题使向量的几何意义初露端倪.
2 神来之笔
例3已知向量a≠e,|e|=1,对任意t∈R,恒有|a-te|≥|a-e|,则
( )
A.a⊥eB.a⊥(a-e)
C.e⊥(a-e) D.(a+e)⊥(a-e)
(2005年浙江省数学高考试题)
解法1由|a-te|≥|a-e|,得
|a-te|2≥|a-e|2,
展开并整理得
t2-2a·et+2a·e-1≥0.
又由t∈R,得
Δ=(-2a·e)2+4-8a·e≥0,
即
e·(a-e)=0,
于是
a⊥(a-e).
故选C.
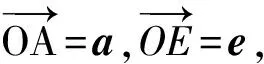


评析作为选择题的压轴题,解法1用代数方法借助函数思想解决;解法2却妙在“图画完,题解好”,即“点到直线的距离是连结点与直线上的点的线段的长度的最小值”,堪称“神来之笔”.
3 平中见奇
例4设向量a,b,c满足a+b+c=0,(a-b)⊥c,a⊥b,若|a|=1,则|a|2+|b|2+|c|2的值是________.
(2006年浙江省数学高考试题)
解法1由(a-b)⊥c,a⊥c,得
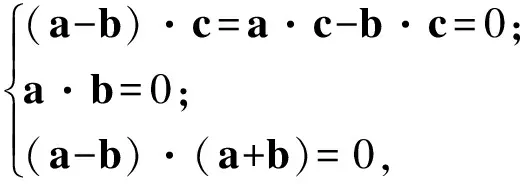
即
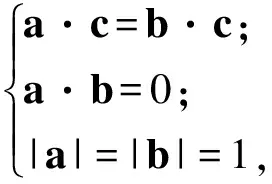
得
|c|2=(-a-b)2=2,
故
|a|2+|b|2+|c|2=4.
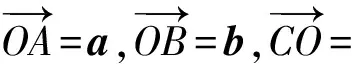
评析代数的运算需要技巧(解法1);根据几何意义构造正方形,则使问题迎刃而解(解法2).题虽平常,却平中见奇.
4 妙趣横生
例5若非零向量a,b满足|a+b|=|b|,则
( )
A.|2a|>|2a+b| B.|2a|<|2a+b|
C.|2b|>|a+2b| D.|2b|>|a+2b|
(2007年浙江省数学高考试题)
解法1由|a+b|=|b|,得
(a+b)2=b2,
即
a2+2a·b=0.
从而
(2a)2-(2a+b)2=-4a·b-b2,
于是
(2b)2-(a+2b)2=-4a·b-a2=a2=
-a2<0,
即
|2b|>|a+2b|.
故选C.
解法2如图1所示,构造△OAC.由题意得
|OB|=|AB|=|BC|,
则△OAC为直角三角形,从而|OC|<|AC|.故选C.
评析此题在2007年影响深远,很多学生感觉无处着手.解法1利用模的运算,用代数方法进行转化,思路清晰,但运算较繁;解法2却以构造直角三角形为契机,关系简单明了,将直角三角形的性质发挥得淋漓尽致,妙趣横生.
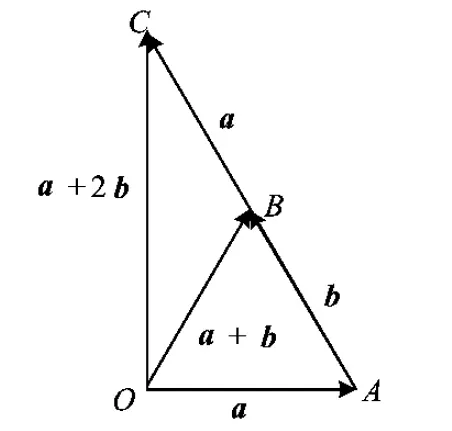
图1
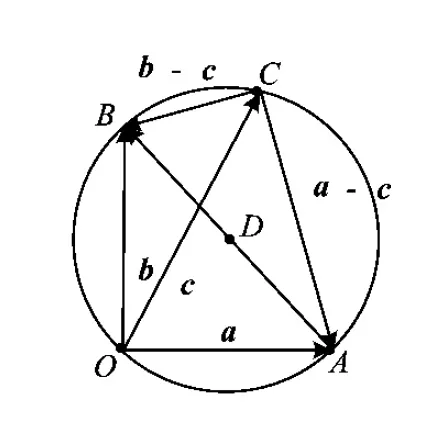
图2
5 各显神通
例6已知a,b是平面内2个互相垂直的单位向量,若向量c满足(a-c)·(b-c)=0,则c的最大值是
( )
解法1由a·b=0,得
(a-c)·(b-c)=c2-(a+b)·c=0,
即
c2=(a+b)·c.
于是
|c|2=|a+b|·|c|cos

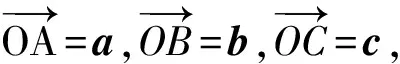
评析代数运算和几何意义各有千秋,各显神通.
数学课程标准强调“向量是近代数学中重要和基本的数学概念之一,它是沟通代数、几何与三角函数的一种工具,有着极其丰富的实际背景”.向量是沟通代数与几何的一座天然桥梁,它集数形于一身,兼具代数性和几何性.在数学中,有2座沟通代数与几何的桥梁:向量和坐标系.坐标系依赖于原点的选择;向量的优越性在于可以不依赖原点,空间中每一点的地位是平等的,因此它比坐标系更一般、更重要.一方面,通过向量的运算可以解决几何中的问题.譬如2条直线是否垂直的问题就可以转化为2个向量的数量积是否为0的问题,这就实现了利用代数方法来解决几何问题.另一方面,对于代数问题,通过向量可以给予几何的解释.譬如2个向量的数量积为0,说明这2个向量所表示的直线是相互垂直的等等.向量代数性质的几何意义对于运用向量刻画几何对象是非常重要的.因此,在教学中应注意揭示向量代数性质的几何意义,帮助学生将向量代数运算与它的几何意义联系起来,使学生能运用向量代数性质更好地刻画几何对象,体会代数与几何的联系.例如:λa的几何意义是与a平行的向量,也可以表示一点和一个方向向量a所确定的直线,2个不共线向量a与b的线性组合λa+μb表示a与b所确定的平面,这就把向量的线性运算与直线、平面联系起来了;a·a的几何意义就是a的长度的平方,这就把向量的数量积运算与向量的长度联系起来,从而把向量的数量积运算与两点间的距离公式联系起来了;a·b=0的几何意义是a与b垂直,这就把向量的数量积运算与向量的位置关系联系起来,从而也就把向量的数量积运算与直线的位置关系以及点到直线的距离联系起来了;设e是单位向量,则a·e表示a在单位向量e上的投影的长度,这就把向量的数量积运算与向量夹角的三角函数联系起来了.
最后,以2010年浙江省数学高考理科试题第21题为例,来看看向量在解决解析几何问题时的妙用.
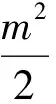
(1)当直线l过右焦点F2时,求直线l的方程;
(2)设直线l与椭圆C交于点A,B,△AF1F2,△BF1F2的重心分别为G,H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.