起点低 入口宽 方法多 能力强——2010年数学高考中有关数列的试题评析

● (三山高级中学 浙江慈溪 315300)

2010年全国各地高考数学试卷共19套37份，与数列有关的题目共64道，分值约占总分的10%.试题既考查了等差数列和等比数列的定义、通项公式、前n项和公式、数列的基本性质、数列求和等基本知识和基本运算，同时又考查了数列与其他内容的综合，以及递推思想、化归思想、归纳能力、运算能力、推理论证能力等.

1 命题特点和知识类型

1.1 命题特点

文、理有别，主要表现在选择题、填空题中文、理不同题，若同题，则试题位置文科较后，理科较前(文、理合卷除外)，解答题文科为16道，理科为14道.文、理要求不同，难度差异大.

1.2 知识类型

数列题在新课程高考卷中所占比例比在非新课程高考卷中的要大，非新课程高考卷无填空型数列题，新课程高考卷中有一半的省市有填空型数列题.选择题、填空题大都以考查等差数列、等比数列的基础知识为主，大部分是容易题或中档题.

2 亮点扫描

2.1 重视基本概念、基本运算，注重通性通法

无论是新课程高考卷还是非新课程高考卷，对等差数列、等比数列的定义，通项公式，求和公式等基本概念、基本运算的考查，依旧是2010年数学高考“数列热点”中的重点.题型分布极为广泛，一般表现在客观题或主观题的第(1)小题，其难度不大，平时应注重通性通法，不搞特技.

( )

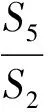
A.11 B.5 C.-8 D.-11

(2010年浙江省数学高考理科试题)

解设公比为q.由

8a2+a5=0，

得

8a2+a2q3=0，

而an≠0，解得q=-2，因此

故选D.

类似的题目还有：辽宁省数学高考文科试题第3题、辽宁省数学高考理科试题第6题、安徽省数学高考文科试题第5题、重庆市数学高考理科试题第1题、北京市数学高考理科试题第2题等,这些都是基础题，题号均靠前，只要合理地运用定义、公式进行仔细计算即可解决此类问题.

2.2 重视性质的考查，注重灵活运用

等差、等比数列的“项的性质、和的性质”是考查对等差、等比数列理解及灵活应用的主要载体.凡是用性质可解的问题一般可用基本量的方法来解决，但在速度与准确度上会拉开距离，因此要注重性质的灵活运用.

例2已知各项均为正数的等比数列{an}，a1a2a3=5，a7a8a9=10，则a4a5a6=

( )

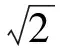
(2010年全国数学高考理科试题Ⅰ)

解由等比数列的性质知

因此

故选A.

类似的题目还有：全国数学高考理科试题Ⅱ第4题，重庆市数学高考文科试题第2题，天津市数学高考理科试题第6题，广东省数学高考理科试题第4题、文科试题第4题等，都是以等差、等比数列的性质为主要考点、恰当结合基本量的方法求解的.

2.3 关注数列与归纳推理

非新课程高考对于推理与证明并没有独立成章，而是把它作为一个数学思想渗透到各个分支.数列是培养学生归纳推理能力的有效载体，让学生多接触一些关于数列的新题和新事物，对培养学生发现问题的能力、发展学生的创新意识有着积极的推进作用.

解观察Tn的数据特点，易归纳猜想出：

类似的题目还有：陕西省数学高考文科试题第11题、浙江省数学高考文科试题第14题、陕西省数学高考理科试题第12题、湖南省数学高考文科试题第20题等.

2.4 文科常规题型出现，稳定送分设计

文科对数列的考查要求比较低，常见的题型有：等差、等比数列的5个基本量的运算，等差、等比数列的证明，简单的数列求和问题等.试题位置相对比较靠前，是命题者在设计中认为考生应该得分的内容，在平时教学中应加强解题规范和正确率的培养.

例4已知等差数列{an}满足：a3=7，a5+a7=26,{an}的前n项和为Sn.

(1)求an及Sn；

解(1)设等差数列{an}的公差为d.因为

a3=7，a5+a7=26,

所以

解得

a1=3,d=2，

于是

an=3+2(n-1)=2n+1,

从而

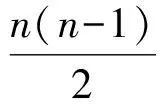
(2)由第(1)小题知an=2n+1，因此

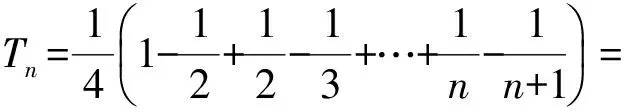
类似的题目还有：陕西省数学高考文科试题第16题、全国数学高考文科试题Ⅱ第18题、重庆市数学高考文科试题第16题、浙江省数学高考文科试题第19题、北京市数学高考文科试题第16题等.

2.5 理科交汇整合呈现，综合应用把关

数列与函数、导数、不等式等知识的有机结合，是数列与其他分支领域的典型的交汇题.既能凸显函数、不等式是高中数学的重点、难点，导数是新课程高考的热点，又能考查学生对数列的综合应用，是高考数列综合题的一大特色，是每年高考的把关题之一.

(1)当a=0时，求通项an.

(2)是否存在a，使数列{an}是等比数列？若存在，求a的取值范围；若不存在，请说明理由.

分析本题主要考查了导数的运算、导数与单调性的关系、等比数列的通项公式、简单的递推数列、不等式的证明、分类讨论、转化与化归的思想方法，解答过程略.

类似的题目还有：重庆市数学高考理科试题第21题、全国数学高考理科试题Ⅰ第22题、湖北省数学高考理科试题第21题等.

3 复习建议

纵观2010年全国各地数学高考试卷，在复习备考中应注意以下几点：

(1)数列问题基本做到小题考查单一的基础知识，大题重在对重点内容的思维探索，题目起点低、入口宽、方法多.在平时复习中，需扎实掌握等差与等比数列的定义、通项公式、求和公式，对公式要正确记忆、熟练运用，要有效地落实基础知识，全面提高学生的基本解题能力.

(2)注重通性通法，关注数列的项、和的性质的灵活应用.

(3)关注数学本质，渗透分类讨论思想和化归思想等数学思想方法，培养抽象概括能力、推理论证能力、运算求解能力以及应用意识和创新意识，促进知识理解与运用，能借此提升并概括具有一般性的思想与方法.

(4)重视学生的参与和自我总结.考生是直接参与考试的，教师只是学生身边的点拨者，在复习中，必须有学生的参与和教师的小结概括.要做到：课堂中内容少讲一些，学生自主探究多一些，可以适当地为个别问题设置一些探索阶梯.学生要多练练、多体会.