通俗易懂 注重通法 优美结论——2010年浙江省数学高考理科试题第21题体验

● (湖州中学 浙江湖州 313000)

笔者通过对2010年浙江省数学高考理科试题第21题的深刻体验,得出了如下启示.现整理出来,以供参考.

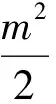
(1)当直线l过右焦点F2时，求l的方程.

(2)设直线l与椭圆C交于点A，B，△AF1F2，△BF1F2的重心分别为G，H.若原点O在以线段GH为直径的圆内，求实数m的取值范围.

1 命题思路探寻

第(1)小题考查椭圆的几何性质；第(2)小题主要考查了直线与椭圆、点与圆的位置关系.此题还同时考查了解析几何的基本思想方法和综合解题的能力.

2 考生答题反馈

第(1)小题大部分学生都觉得很容易，通过椭圆的几何性质，利用点在直线上建立方程求实数的值，从而得到直线的方程.但是第(2)小题要通过建立不等关系求出实数的取值范围，很多学生忽略了二次方程判别式大于0这个条件，或者无法通过条件“点O在以线段GH为直径的圆内”来建立相应的不等式.

3 巧妙解题方法

一般地，直线与椭圆相交于点A,B，则联立直线与椭圆的方程，消去y得到关于x的二次方程.在判别式大于0的前提下，利用韦达定理得xA+xB和xAxB，再利用直线方程得到yA+yB和yAyB.接下来就是如何量化以下2个已知条件：(1)△AF1F2，△BF1F2的重心分别为G，H；(2)点O在以线段GH为直径的圆内.

因为原点O是边F1F2的中点，所以AO是一条中线，因此

即

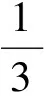
同理可得

这样条件(1)得以解决.

对于条件(2)，有以下3种解法：

(1)利用定义：若1个点与圆心的距离小于半径，则该点在圆内.

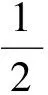
(2)利用圆的方程判断点与圆的位置关系.

在必修2“直线与圆的方程”的教学过程中，利用圆的方程来判断点与圆的位置关系，体现了解析几何的本质.先将圆方程化为右边为0的方程，然后将点的坐标代入圆方程的左式，看其符号：若为正，则点在圆外；若为0，则点在圆上；若为负，则点在圆内.而以GH为直径的圆方程为

(x-xG)(x-xH)+(y-yG)(y-yH)=0.

因为点O在圆内，所以

(0-xG)(0-xH)+(0-yG)(0-yH)<0，

即

xGxH+yGyH<0.

(3)利用向量的数量积.

通过第3种解法，可以发现关于点与圆的位置关系的一个优美的结论：

4 教学思考启示

4.1 做好初、高中教材内容的衔接工作

高中新教材的内容编排是螺旋上升的，并且起到了承上启下的作用，它不仅是初中内容的深化，也为学生进一步深造打下了基础.从初中的平面几何中的圆到高中的平面直角坐标系下的圆方程是一种历史的继承又是数学思想方法的一次飞跃，因此要做好初、高中教材内容的衔接工作.

4.2 注重通式通法的教学

2010年浙江省高考《考试说明(数学)》中明确指出:高考试卷应全面考查“双基”，突出数学主干知识，注重通式通法，淡化技巧.在处理直线与圆锥曲线的位置关系时，应遵循设直线方程、联立方程组、消去其中一个变量、判别式、韦达定理这样的一个解题思路.在处理二元二次方程时，配方法仍是首选.

4.3 重视教材中的课后习题

命题者与学生的共同财富是数学课本.试题以课本为基础，源于课本又高于课本.因此，在考前应回归课本，将定义、定理、公式及相关结论等重点内容熟读备用.

4．4 培养学生综合解决问题的能力

此题是直线与圆的方程和圆锥曲线的综合问题，考查了学生综合解决问题的能力.知识交汇点又是高考命题的一个重点，解法3体现了向量与解析几何的交汇.高考数学试卷的定位就是以能力立意，将知识、能力和素质融为一体，全面检测考生的数学素养.