在知识网络交汇点设计试题——2010年数学高考不等式试题评析

● (湖州中学 浙江湖州 313000)

不等式一直是中学数学的重要内容之一，它渗透到了中学数学课本的很多章节，在实际问题中被广泛应用，可以说是解决其他数学问题的一种有利工具．随着以培养创新精神和实践能力为重点的素质教育的深入发展，高考命题越来越关注开放性、探索性等创新型问题，尤其是与函数、导数、数列、解析几何等综合的不等式证明问题以及涉及不等式的应用题等.

1 教学要求与大纲对比

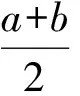
2 命题特点和知识类型

2.1 命题特点

纵观2010年全国及各省市共37套文、理高考试卷，笔者发现对不等式重点考查的有4种题型：解不等式、证明不等式、不等式的应用、不等式的综合性问题(如含参问题、恒成立问题等).这些不等式问题主要体现了等价转化、函数与方程、分类讨论等数学思想．

2.2 知识类型

不等式的解法问题常常出现在选择题中,譬如求最值问题、简单的线性规划问题、含参的不等式恒成立问题、不等式的证明问题.不等式知识在高考中很少单独成题，但作为工具解决问题的作用不会降低，即不等式的工具性；注重知识之间的交叉、渗透和综合，对考生在知识及思维方面的不断转化提出了较高的要求，有较强的综合性和一定的思维深度.

3 亮点扫描

( )

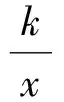
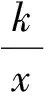
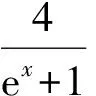
(2010年辽宁省数学高考理科试题)

分析本题将导数的几何意义、求导运算、三角函数和基本不等式知识有机地结合在一起.因为

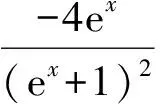
3.2 线性规划问题

( )

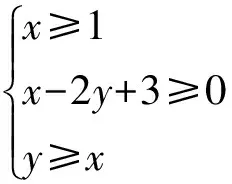
(2010年福建省数学高考理科试题)

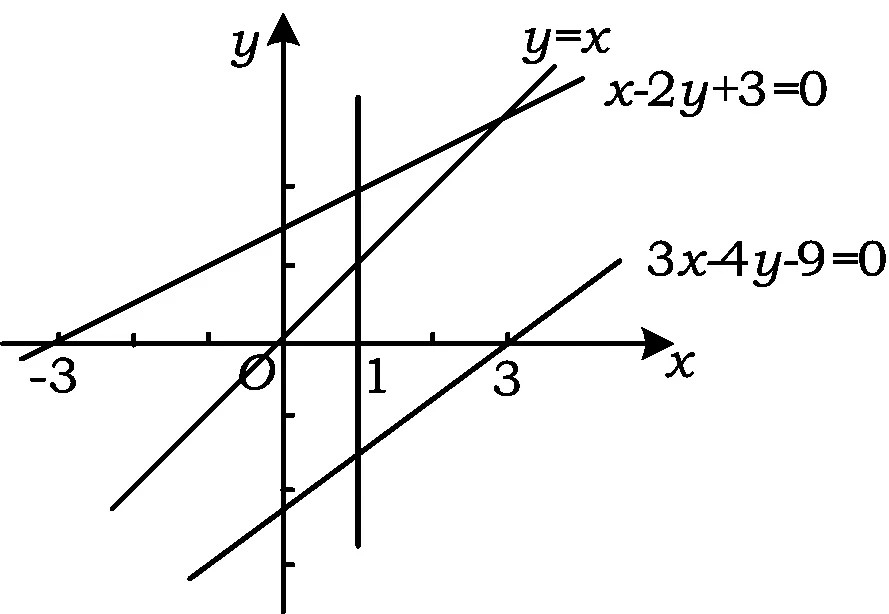
图1

3．3 函数不等式中的高等背景

数学科《考试大纲》指出：“数学科考试，要发挥数学作为基础学科的作用，既重视考查中学数学知识的掌握程度，又注重考查进入高校继续学习的潜能”.

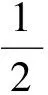
(2010年山东省数学高考理科试题)

分析本小题主要考查导数的概念以及利用导数研究函数性质的能力，考查分类讨论思想、数形结合思想、等价变化思想，以及综合运用知识解读新情境、新问题的能力.

①当a=0时，h(x)=-x+1，x∈(0,+∞)，因此当x∈(0,1)时，h(x)>0,此时f′(x)<0,函数f(x)单调递增；当x∈(1,+∞)时，h(x)<0，此时f′(x)>0，函数f(x)单调递增.

②当a≠0时，由f′(x)=0，即

ax2-x+1-a=0，

解得

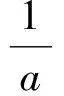
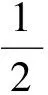
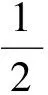
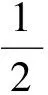
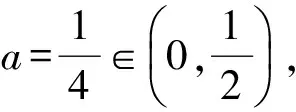
x1=1,x2=3∉(0,2),

①当b<1时，因为

[g(x)]min=g(1)=5-2b>0,

矛盾.

②当b∈[1,2]时，

[g(x)]min=4-b2≥0,

矛盾.

③当b∈(2,+∞)时，

[g(x)]min=g(2)=8-4b,

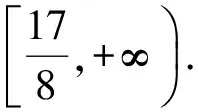
4 复习建议

4.1 改进教学方式

在教学方式的改进中，最重要的是要让学生有积极、独立地进行数学思考的空间.在具体细节上让学生自己多动手、多阅读、多思考、多交流，让学生多发表意见.教师可参与到学生的活动中去，多听少讲，在关键点上让学生有机会提出自己的见解.课堂教学应加强问题引导学习、教学重心前移、典型丰富例证、提供概括时机、保证思考力度、加强思想联系、使用变式训练、强调反思迁移.

4.2 追求有效教学

有效的课堂教学关键是要解决好让学生想学、能学、会学、学好这样一系列的问题，使学生真正参与到学习活动中来，使教和学的各个环节紧密衔接，相互适应，并能取得最大效益和最佳效果.在当前客观的教学形势下，一问就会、一答就对的演示性课堂并不是我们的追求.结合自身的教学经历，笔者认为要提高高三数学复习的有效性，抓住“3个有效”是重点：教学理念有效、教学方式有效、教学过程有效.

通常复习课上有一个突出的矛盾，就是时间太紧，既要处理足量的题目，又要充分展示学生的思维过程，二者似乎很难兼顾.我们可采用“焦点·感悟法”解决这个问题，大多数题目其解法是“入口宽，上手易”，但在连续探究的过程中，常在某一点或某几点上搁浅受阻，这些点被称为“焦点”，其余的则被称为“外围”.我们大可不必在外围处花精力和时间去进行浅表性的启发诱导,而只要在焦点处启发学生探寻突破口，通过感悟集中学生的智慧，让学生的思维在关键处闪光、能力在要害处增长、弱点在隐蔽处暴露、意志在细微处磨砺.

4.3 宜“广积粮”而非“深挖洞”

由《考试大纲》所提供的命题原则——“在知识网络交汇点设计试题”，考查能力的题目往往是几个重点和热点内容的有机组合，其实它们都来自于简单题.在备考过程中，不需要“深挖洞”——在各个考点上向深度、难度进军，而只需“广积粮”——系统掌握知识，再综合运用之.