理解基础知识 掌握基本方法 运用解题策略——2010年浙江省数学高考文科试题第18题解读

● (豫才中学 浙江绍兴 312000)

解三角形题是考生必攻之第一大题.取下此题意义非同凡响，因此关于第一大题的命题思路、答题情况、化解方法、教学启示就成为了众多考生和教师努力探寻的目标和方向，下面从这4个方面透视解三角形大题．

(1)求角C的大小；

(2)求sinA+sinB的最大值.

下面给出该题的标准答案.

解法1(1)由

可得

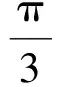
(2)sinA+sinB=sinA+sin(π-C-A)=

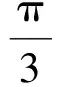
1 命题思路探寻

对于解三角形命题的基本思路是考查解三角形的2个基本定理，即正弦定理、余弦定理;考查三角函数的图像和性质.2010年浙江省数学高考第一大题的命题从考查正弦定理的三角形面积公式入手，又兼考查余弦定理的逆用，再求据特殊三角函数值求角.仅第(1)小题就实现了“三考”；对于第(2)小题则采用2个和差求最值.求解的方法既可从角求最值，也可结合基本不等式求最值,可谓“一标多路”型问题，可考查考生灵活掌握三角函数的解题技巧和解题能力．

2 考生答题反馈

对于该题的第(1)小题,有的学生虽然解题成功但花时不少，有的学生甚至因公式错用，特殊三角函数值记错而造成遗憾；第(2)小题的破解有相当的学生因采用“合一变形”而不知两角的和而无法适从,从而导致无法求解最大值，有的也是凭猜想才求得.当然,该题有相当多的学生是求解成功的．

3 巧妙解题方法

该题参考答案的方法运用恰当，是多数学生的求解方法.下面3种方法有的虽有雷同且略有巧妙，有的虽方法笨拙但也为出路，有的则逢山开路、独辟蹊径．

解法2(化解归一法)

(1)同解法1

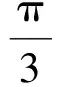
点评此解法与标准答案雷同，也是通过化二角为一角的基本思路,不同的是化角为B，合一变形时采用了化为余弦值求解.但方法之间显示出解题者对于基础知识、基础方法的娴熟．

解法3(拆角转化法)

(1)同解法1.

(2)sinA+sinB=

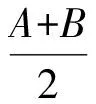
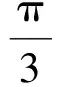
点评这一方法源自于大纲版的和差化积公式，课本上虽有提及但不作要求.若能参悟化角技巧和方法则不失为一智慧之举.当然,有的教师可能对学生进行了补充和讲解，使其得心应手．

解法4(化角为边法)

(1)同解法1.

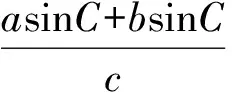
不妨令t=sinA+sinB,则

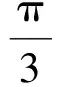
即

ab=a2+b2-c2,

因此

当且仅当a=b时,等号成立，则

点评化角为边法是考生在遇困境时的一种拼博.从方法的破解思路上可见解题者的勇气和胆略，也可见解题者具有逢山开路、遇水架桥的本领，更可见解题高手的智慧和策略．

4 教学思考启示

对于第一大题的求解肯定是考生必争之分，如何顺利求解通过以上3个方面的总结可得“理解基础知识”、“掌握基本方法”、“运用解题策略”3个启示．

(1)理解基础知识．三角函数图像和性质、解三角形的有关知识是这一大题所涉及的基础知识，涉及到的公式较多，既有三角恒等变换公式，也有正弦定理、余弦定理，更有“合一变形”、正弦定理面积公式、知角求值和知值求角等基本知识．因此理解好这些基础知识，做到基础知识运用时既可顺用、逆用，甚至可变形用，这样才能让知识变活，使考生理解基础知识，成为知识运用的主人．

(2)掌握基本方法．该大题涉及到的方法众多，既有公式直接求解法，也有合一变形化简法、数形结合法、分类讨论求解法、转化化归法等.在必要时,还可结合基本不等式性质、放缩法等技巧进行破题．

(3)运用解题策略．该大题在化解时若有一个全局策略，则可节省解题的时间且成功率提高.若第(1)小题结合公式形态采用公式逆用求角,第(2)小题采用化两角为一角求最值，则思路清晰、解题方法得当、成功率就高；反之若不采用较好的策略则易误入歧途，没有很好的解题实力就可能惨败．