资本资产定价模型在上证市场的实证研究
2010-11-06李璁陈荣达
李璁,陈荣达
(浙江财经学院金融学院,浙江杭州 310018)
资本资产定价模型在上证市场的实证研究
李璁,陈荣达
(浙江财经学院金融学院,浙江杭州 310018)
选用2003.1-2009.12期间上证市场交易所选取的20支股票的月收益率数据,通过bjs检验验证capm模型在上证市场的有效性。现实结果与capm模型严重不符,这不仅体现上证市场的不成熟,也体现capm模型的假设条件与现实差距太大,因此capm模型在实际应用时应谨慎对待其有效性。
资本资产定价模型(capm);实证检验;有效性
1 资本资产定价模型简介
从Markowitz和Tobin提出资产组合理论开始,现代资本理论迅速发展,其中最重要的理论包括了Sharp[2]、Lintner[3]和Mossin[4]发展的资本资产定价模型(CAP M)。该定价模型提出高期望收益往往和高风险相关联。简单来说,资产超过无风险利率的预期超额收益率与以β值度量的资产面临的未分散的市场风险线性相关。
尽管资本资产定价理论在现代资产定价理论中一直占领着统治地方,但是由于CAP M模型是在一组苛刻的假设条件下建立的,一直不断出现一些实证研究的成果对资本资产定价模型的有效性提出了质疑。国外有Tinic、West和Basu[5],国内有阮涛、林少宫[6]和李和金、李湛[7],结果表明,不论美国股市还是中国股市都不支持严格的CAP M模型。
2 实证检验
2.1 样本数据选取
本文选取2003.1-2009.12作为研究时间段,该时间段体现了熊市和典型牛市的波动特征。选取的样本是从上证股票市场随机挑选的20只股票,利用其在样本时间段的84个月度收益率数据进行分析。在此不选取日度数据或周度数据是由于相对的高频数据导致了噪声数据的使用,有损系数估计的效率。另外,用上证综合指数的月收益率作为市场组合收益率(数据均来自CCER经济金融研究数据库),并将各个时间段对应的一年期定期存款利率作为无风险利率(数据来自中国人民银行),实际运算中将年利率换算成月利率。
2.2 检验方法
对CAP M模型的实证检验方法有很多,本文选用Black、Jenson和Scholes的方法(简称BJS检验)进行分析检验。
第一步利用2006.1-2008.12的月数据估计单个股票的β系数,系数值通过单个股票月度收益率对市场组合月收益率的回归来估计。如下式:

其中,
Rit股票i在t时刻的月收益率(i=1,2,…,20);Rft代表无风险收益率;Rmt是市场组合在t时刻的月收益率;βi是对股票i的β系数估计;eit是误差项。
第二步则是将股票按照β系数大小排序,将20支股票分为10组,每组包含两只股票,每只股票赋相同权重,并利用2003.1-2005.12的样本数据计算组合的月收益率,组合月收益率取组合内股票收益率的算术平均。然后通过组合月收益率对市场组合月收益率回归估计组合的β系数:
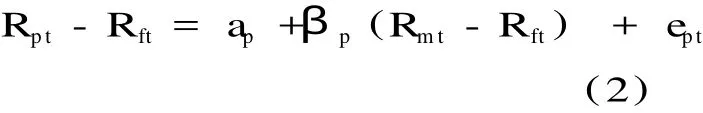
其中,
Rpt股票组合p在t时刻的月收益率(i=1,2,…,20);Rft代表无风险收益率;Rmt是市场组合在t时刻的月收益率;βp是对股票组合p的β系数估计;ept是误差项。
第三步利用2009.1-2009.12的组合月平均收益率对上步得出的组合β值进行横截面回归,对收益与系统风险关系进行检验:

其中,Rp为组合的月平均收益率;βp为组合的β系数;εp为误差项。
3 实证结果及分析
在置信水平95%下,利用等式(1)对股票的β值进行估计(见表1),表中β系数的估计值均通过t检验,估计值显著,利用其大小排序分为10组股票。
表1 单个股票的β值估计

表1 单个股票的β值估计
股票名称β股票名称β武钢股份1.538711宇通客车0.908576葛洲坝1.09803同仁堂0.721116中视传媒0.962209永鼎股份0.880745亚盛集团1.101715金健米业0.907288菲达环保0.661829两面针1.527042江西铜业1.531689中金黄金1.290523山鹰纸业0.849112南纺股份0.900147华联综超0.881226鲁抗医药0.853614新世界0.767021杉杉股份1.188925赛马实业0.988985华电能源0.886169
分组完成,即可利用等式(2)对组合β系数进行估计,结果如表2所示

表2 组合β系数估计

7赛马实业葛洲坝0.9568190.1695038.324525 8亚盛集团杉杉股份1.1021680.1745736.313495 9中金黄金两面针1.2507030.2230615.606997 10江西铜业武钢股份1.2519810.2093775.979563
结果显示,组合β估计的标准误差较小,t检验值均大于临界t值,t检验显著,组合β显著不为零,可继续进行横截面回归。利用等式(3)进行横截面回归,得表3:
表3收益和系统性风险回归系数T检验值R2Fγ00.0309701.8335250.2958873.361815γ10.0410811.265182横截面回归主要为检验高系统性风险是否与高期望回报率相关联。但结果显示γ0的t检验小于t0.025(8)=2.306,表明无风险利率不明显异于零,意味着市场投机需求过大;γ1系数略大于零,但t检验也小于2.306,表示收益和系统性风险之间的正线性关系不显著,加上F检验值小于F0.05(1,8)=5.32以及拟合优度R2=0.295887,这都表明方程拟合效果不理想,总体显著性不够,高系统性风险与高期望回报率关联性不强。
4 结论
实证检验结果与资本资产定价模型有明显的差异,这可能是由于选样的偏差和样本量大小差异造成统计推断偏差从而导致实证结果背离资本资产定价模型。但主要原因应该是资本资产定价模型的三大异常苛刻的假设,严重脱离现实,在现实市场上风险偏好不同的投资者和投机者在投资决策和投资行为上差异明显,而且由于中国证券市场监管体系尚不健全,导致市场投机气氛过重、交易及监管成本过高,致使资本资产定价模型在实际应用容易出现偏差,因此,基于CAP M模型在尚不成熟的上证市场的应用缺乏有效性依据。但是,资本资产定价理论对于现代资本理论及应用所独特的引导作用是不容忽视的,我们在实际应用时应严谨对待。
[1]Black,F.Jensen,M.C.and Scholes,M.The Capital asset pricingmodel:Some empirical tests[J].Studies in the Theory of CapitalMarkets.45(1972),79-121.
[2]Sharpe,W.Capital asset prices:a theory of market equilibrium under conditions of risk[J].Journal of Finance,33(1964),885-901.
[3]Lintner,J.The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets[J].Re2 view of Economics and Statistics,47(1965),13-37.
[4]Mossin,J.Equilibrium in a capital assetmarket[J].Econometrica,34(1966),768-783.
[5]SehaM.Tinic,Richard R.West.Risk and Return:January and the Restof the Year[J].Journal of Financial Economics,13(1984),561-574.
[6]阮涛,林少宫.CAPM模型对上海股票市场的检验[J].数理统计与管理,2000,(19).
[7]李和金,李湛.上海股票市场资本资产定价模型实证检验[J].预测,2000,(05).
[责任编辑:李成文]
F123
A
1004-7077(2010)03-0112-03
2010-03-28
李璁(1987-),男,湖南汉寿人,浙江财经学院金融学院金融学硕士研究生,主要从事金融工程与金融风险管理研究。陈荣达(1972-),男,浙江温州人,浙江财经学院金融学院副教授,主要从事金融工程与金融风险管理和公司金融研究。
