利用线性规划方法求解企业利润最大化问题
2010-10-24贾慧田京
贾慧,田京
(山西电力职业技术学院,山西 太原 030001)
利用线性规划方法求解企业利润最大化问题
贾慧,田京
(山西电力职业技术学院,山西 太原 030001)
论文针对企业在人力物力资源限定的条件下如何获得最大利润的问题,提出了运用线性规划的方法,提高了企业的工作效率和决策的正确性。
线性规划;企业;利润最大化
企业是盈利性的经济组织,追求利润是其根本目标。在日常的生产生活中,如何获得最大的利润是每一个企业生存发展的关键,而企业要想达到利润最大化通常可以采用两种方法:一是改进生产技术,如引进新的生产方式和工艺,使用生产效率更高的新设备或新型的原材料以提高单位时间内的产出;二是改进生产组织与计划,即合理地安排利用企业现有的人力和物力资源,在不增加生产投入的基础上,通过提高各种资源的利用率来达到企业利润的最大化。
两种方法相比较,第二种方法在成本不变的前提下提高了产出率,使各种有限的资源得到了最大的利用,从而提高了企业利润,非常受企业的欢迎。这种如何在给定的条件下,合理地安排与企业生产有关的人力和物力资源,使企业的利润达到最大化的问题属于运筹学中的线性规划问题。
一、线性规划
线性规划是运筹学中的一个重要分支,它研究比较早、发展比较快、应用非常广泛,是辅助人们对生产生活进行科学化管理的一种数学方法。凡是求线性目标函数在一定的线性约束条件下的最大值或者最小值的问题,都属于线性规划的研究范围。线性规划广泛应用于工程技术、经济分析、经营管理等方面,它能在人力、财力和物力等资源有限的条件下,帮助企业的决策者做出最优决策,并为其提供科学依据。
线性规划的要素主要包括决策变量、约束条件和目标函数。
二、建立线性规划模型的方法
在解决企业的实际线性规划问题时,应先根据生产情况建立线性规划模型,步骤如下:(1)根据能够影响所要达到某一目的的因素来确定决策变量;(2)根据决策变量与所要达到目的之间的函数关系来确定目标函数;(3)根据决策变量所受的限制条件来确定决策变量应满足的约束条件。
三、线性规划模型的特点
1.每个模型都含有若干个决策变量“x1,x2,x3……xn”,其中n为模型中决策变量的个数。决策变量的每一组取值都表示一种方案,决策变量的值一般都是非负的。
2.目标函数必须是以决策变量为自变量的线性函数,根据实际情况可以求解最大化(max)问题或最小化(min)问题,二者统称为最优化问题。
3.约束条件也必须是以决策变量为自变量的线性函数。
当所建立的数学模型的目标函数为线性函数,约束条件为线性等式或者不等式时,称此数学模型为线性规划模型。
四、应用举例
1.提出问题
假设某企业生产A、B两种产品,每生产一个A产品,需要耗费60公斤煤、50公斤铁、40公斤水,可以获利1.2万元;每生产一个B产品,需要耗费30公斤煤、80公斤铁、60公斤水,可以获利1.8万元。目前企业可用的各种资源额度为:煤5400公斤、铁4800公斤、水6000公斤,请计算该企业要生产多少A产品和B产品,才能使企业的利润达到最大化?
2.建立线性规划模型
(1)确定决策变量
在该模型中能够影响企业利润的因素为A产品和B产品的产量,因此将A产品和B产品的产量确定为该模型的决策变量,设需要生产A产品X1个,生产B产品X2个。
(2)确定目标函数
设企业的利润为Z,则Z与X1、X2的函数关系为:Z=1.2X1+1.8X2
(3)确定决策变量应满足的约束条件
题中告知目前企业可用的各种资源额度为:煤5400公斤、铁4800公斤、水6000公斤,依题意可设置如下约束条件:
60X1+30X2≤5400;50X1+80X2≤4800;40X1+60X2≤6000。
3.选择规划求解工具
常见的线性规划求解工具有MATLAB优化工具箱和Excel规划求解工具,但对于大多数企业的决策者来说,MATLAB优化工具箱专业性太强,不容易理解和掌握,而Excel规划求解工具则相对容易得多,只要经过简单的学习就可以掌握,因此在求解简单的线性规划问题时,大多数企业都倾向于使用Excel规划求解工具。
4.安装Excel规划求解工具
企业的应用人员在安装Microsoft Office时,若选择“完全安装”,则安装完成后在Excel的“工具”菜单中可以直接找到“规划求解”命令项;若选择“定制安装”,则可以在安装过程中选择安装“规划求解”模块,安装完成后在Excel的“工具”菜单中也可以找到“规划求解”命令项;若选择“典型安装”,则安装完成后在Excel的“工具”菜单中无法找到“规划求解”命令项,需要再添加该模块。
添加“规划求解”模块的方法:单击Excel的“工具”菜单,在弹出的下拉菜单中选择“加载宏”选项,此时会出现一个名为“加载宏”的对话框,然后在“可用加载宏”列表框中选择“规划求解”复选框,单击“确定”即可。经过如上操作后,Excel的“工具”菜单中就可以找到“规划求解”命令项了。
5.解决问题
(1)根据线性规划模型建立工作表(如表1)所示
在表2的工作表中,单元格B10用来存放产品A的生产数量,C10用来存放产品B的生产数量,B11为目标单元格,用来存放目标函数的值(最大利润Z的值),E6:E8存放约束条件的计算公式。
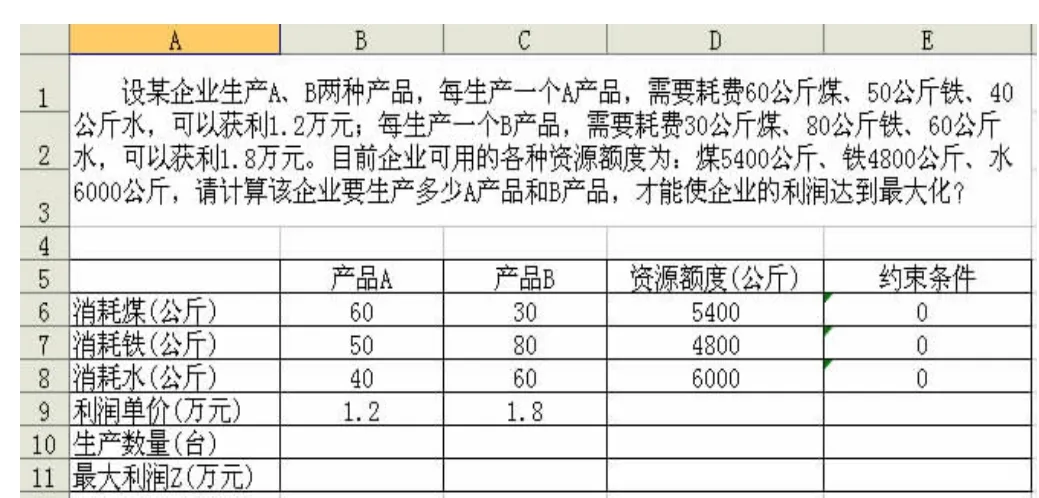
表1 规划求解初始工作表
在表1的相关单元格中输入下列公式:
E6=SUMPRODUCT(B6:C6,B10:C10);
E7=SUMPRODUCT(B7:C7,B10:C10);
E8=SUMPRODUCT(B8:C8,B10:C10);
B11=SUMPRODUCT(B9:C9,B10:C10)。
(2)利用Excel规划求解工具求解
单击Excel“工具”菜单,在弹出的下拉菜单中选择“规划求解”,打开“规划求解参数对话框”。
①在打开的对话框中设置“目标单元格”为“$B$11”;设置“等于”项目为“最大值”;设置“可变单元格”为“$B$10:$C$10”。
②添加约束条件。在“约束”项目中单击“添加”按钮,弹出“添加约束”对话框,在该对话框中设置“单元格引用位置”为“$E$6”,关系运算符为“<=”,“约束值”为“$D$6”,单击“确定”按钮,第一个约束条件添加完成,依次类推添加其余两个约束条件。
③求解。单击右侧的“求解”按钮,Excel会自动对决策变量和目标函数进行求解,并弹出规划求解结果对话框。其中显示“规划求解找到一解,可满足所有的约束及最优状况”,在其下的单选列表框中选择“保存规划求解结果”,单击“确定”,相应的结果即可显示在可变单元格和目标单元格中(如表2所示)。可变单元格$B$10的值代表需要生产产品A 87个,$C$10的值代表需要生产产品B 5个,目标单元格$B$11的值代表在相应的资源额度限制下可以获得的最大利润为114.5万元。
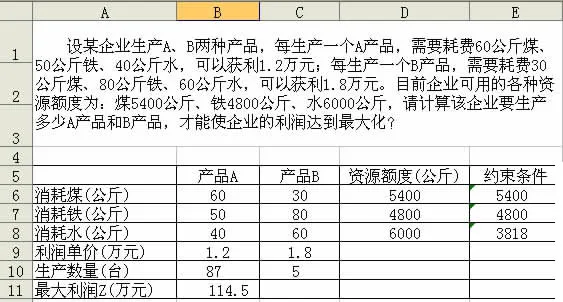
表2 规划求解结果显示表
[1]孙中红,胡喜玲,于洪章,隋洪.Excel软件求解线性规划和某些数学问题的方法[J].烟台师范学院学报(自然科学版),2005,(1):26-28.
[2]叶艺林,程秀芳.用“规划求解”工具求解线性规划[J].景德镇高专学报,2006,(4).
[3]吴祈宗.运筹学[M].北京:北京机械工业出版社,2002.
[4]裘敬华,刘岩.用 Excel处理规划最优问题探讨[J].黄河水利职业技术学院学报,2005,(2).
F27
A
1673-0046(2010)11-0079-02
