不同理性双寡头博弈市场的动态演化研究
2010-10-09潘玉荣贾朝勇
潘玉荣,贾朝勇
(蚌埠学院 数理系,安徽 蚌埠 233030)
不同理性双寡头博弈市场的动态演化研究
潘玉荣,贾朝勇
(蚌埠学院 数理系,安徽 蚌埠 233030)
对不同理性双寡头博弈市场进行定量分析,通过数值模拟发现随着系统参数的改变,市场将出现分岔、混沌和奇异吸引子等复杂的动力学现象;实验说明一旦市场进入混沌态,它将对初始条件具有敏感的依赖性,从而使得市场变得不可预测.
延时有限理性;Nash均衡;混沌;不同理性
有限理性决策思想认为寡头的生产决策都是基于自己掌握的市场信息做出的.文[1-2]研究了基于有限理性产量调整模型的动态行为,即企业通过考察自身现期的边际利润情况下来决定下一期的产量,结果表明这样的市场动态很复杂,出现了稳定周期的,拟周期的分岔甚至混沌现象.文[3]把溢出效应及非线性成本函数引入有限理性模型中.随着有限理性寡头的数目的增加,市场的状态将会如何变化,文[4]对此做了详细的探索.文[5]引入了延时有限理性,阐述了延时有限理性决策能扩大市场的均衡域.
文[6]的模型主要考虑的是在市场信息不对称的情况下,理性层次不同的个体因为掌握的信息量以及对市场的反应能力不一样采用完全不同的竞产策略,一方采用延时有限理性竞产决策另一方采用最优反应.下面利用数值模拟的方法继续探讨该模型确立的博弈市场的复杂动态.
1 模型简介
模型[6]假设在一个只有两个企业(企业1和企业2)竞争的市场,它们生产一种同种同质商品.市场的价格和需求用一个逆需求函数来表示即:p=f (Q)=a-b Q其中a,b为正常数,a为市场最高价格,p为市场的出清价格,市场的总需求和总供给相同,总供给为:Q=q1+q2,qi为第i个企业的在t时刻的供应量.每个企业的生产成本为一个线性函数Ci(qi) =ciqi(i=1,2),因此各企业的利润函数可以表示为πi(q1,q2)=p qi(t)-ciqii=1,2各企业的边际利润为

考虑在信息不对称的情况下,理性不同的两个企业因为掌握的市场信息量和对市场的反应能力都不一样,它们采用完全不同的竞产策略.企业1将延时有限理性用到产量决策中,考虑以往两期的利润情况来决定下期的产量.它的生产决策是:
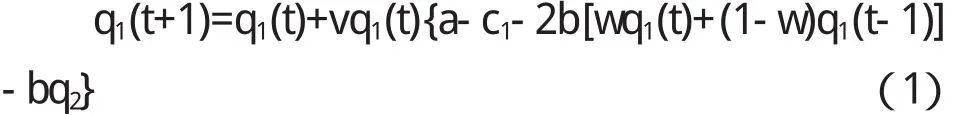
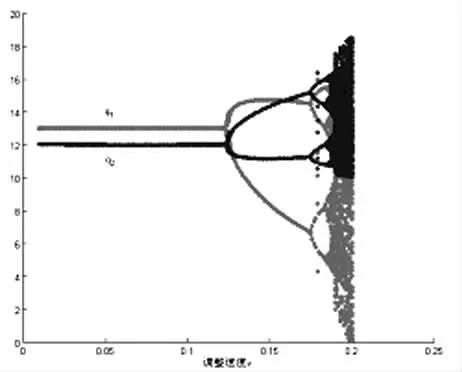
其中w是权重,0 根据(1)、(2)可以得到具有不同理性的两个寡头博弈模型即得以下的二维动力系统 基于经济模型本身的意义,均衡解应为非负解,我们求得的系统(3)均衡点[6]为 其中a>c2,a>2c1-c2且a>2c2-c1.E0为边界均衡点,它是不稳定的点,E*显然是唯一的Nash均衡点,此点是双方反应曲线的交点,根据Jury’s条件可得Nash均衡点的稳定条件[6]为 从(4)式中我们可以清楚的看到系统(3)的稳定对系统参数的依赖性很强.若我们固定参数a,c1, c2,v的值,调整权重w的值,随着w的减小,系统的稳定性增强.若固定参数a,c1,c2,w的值,而企业2的产量调整速度值v增大,系统的均衡点稳定性将受到影响,系统可能出现分岔,陷入混沌态.同样调整系统参数中a,c1,c2中的任意一个的值,系统的稳定性都会受到影响. 图1 q1,q2的稳定解随着v变化的分岔图 为了更好地了解系统(3)的动态行为,本节借助Matlab软件对不同理性的双寡头博弈模型进行数值模拟.设市场参数a=20,b=0.5,两企业的边际成本分别为c1=1,c2=1.5,权重w=0.9,随着具有有限理性寡头企业1调整速度v的不断增大,产量q1和q2出现稳定周期、拟周期的分岔甚至混沌现象(如图1).若固定a=20,b=0.5,c2=1.5和w=1,v=0.18,随着企业1边际成本的不断增大,企业1和企业2的产量各自收敛到一个固定的值(如图2),从图2中可以看到当寡头企业1边际成本c1比较小时,企业1的产量很高,而企业2的产量相比较企业1来说要低一些,且两者的产量都处于混沌态,而当c1较大时企业的产量最终将减少,企业2的产量将增加. 图2 产量q1,q2随着c1变化的分岔图 图3给出系统参数为(a,b,c 1,c 2,v,w)= (20,0.5,1,1.5,0.19,1)时的博弈模型奇异吸引子,它的结构和Henon吸引子很相似. 图3 (a,b,c 1,c 2,v,w)=(20,0.5,1,1.5,0.19,1)时的奇异吸引子 图4 初始产量为(q10,q20)企业2产量时序图 对初始条件的敏感依赖性也是混沌现象的重要特征,为了验证系统(3)是否对初始值具有敏感依赖性,现假定系统参数为a=20,b=0.5,c2=1.5,w=1, v=0.19,若将初始两企业的初始产量的取值为(q10, q20),企业2产量的时序图如图4,当两企业的初始产量取值为(q10+0.0001,q20)时企业2产量的时序图如图5,比较两图发现刚开始寡头企业2的产量差别不大,随着时间的推移,差异不断加大,即初始产量的微小变动对博弈结果产生巨大的变化,由此看出混沌态容易使市场变得不可预测. 图5 初始产量为(q10+0.000,q 20)时企业2产量时序图 本文继续探讨基于不同理性的双寡头博弈模型及由此模型构成的寡头博弈市场的演化动态,通过数值模拟发现随着系统参数的变化,市场将出现出现分岔、混沌等复杂动力学现象,当产量调整速度较大时,两寡头企业的产量出现了奇异吸引子;实验验证不同理性寡头博弈市场对市场的初始条件具有敏感的依赖性即初始条件的细微变化都会对博弈结果发生巨大的影响.以上的模拟结果再一次说明不同理性的双寡头博弈市场演化很复杂,所以有限理性寡头企业要不断注意企业所处环境的变化,适时调整自身策略,尽量避免混沌的不可预测状态. 〔1〕E.Ahamed,H.N.Agiza,S.Z Hassan.On modifications of puu’s dynamical duopoly[J]. Chaos,Solitons&Fractals,2000,11:1025-1028. 〔2〕H.N.Agiza, A.S.Hegazi,A.A.Elsadany, The dynamics of in Bowley’s model with bounded rationality[J].Chaos,Solitons&Fractals,2001,9: 1705-1717. 〔3〕易余胤,盛昭瀚,肖条军.具溢出效应的有限理性双寡头的动态演化[J].系统工程学报,2004,19(3): 244-250. 〔4〕Tönu Puu. On the stability ofcournot equilibrium when the number of competitors increases [J]. Economic Behavior & Organization,2006,16:263-312. 〔5〕M.T.Yassen*,H.N.Agiza .Analysis ofa duopoly game with delayed bounded rationality [J]..Applied Mathematics and Computation. 2003,138:387-402. 〔6〕潘玉荣,贾朝勇.不同理性双寡头博弈模型的复杂性分析[J].复杂系统与复杂性科学,2007,2(4): 71-76. F244 A 1673-260X(2010)08-0053-03 安徽省高等学校优秀青年教师人才科研基金项目(2010SQRL115)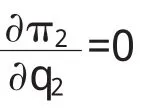
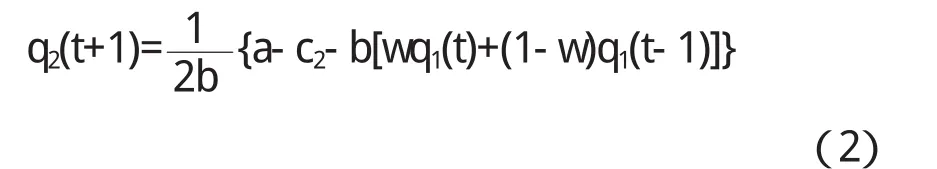
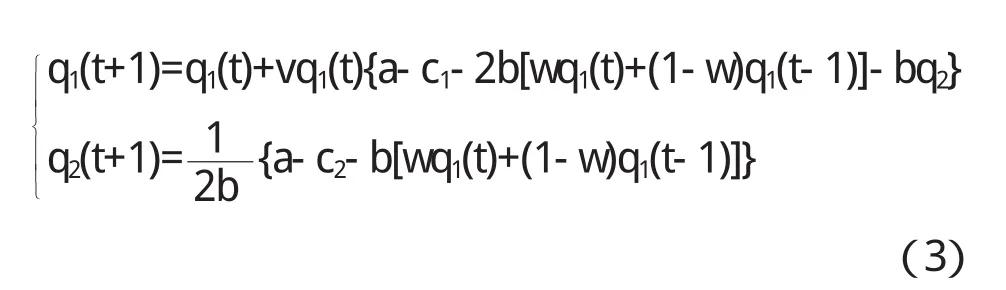
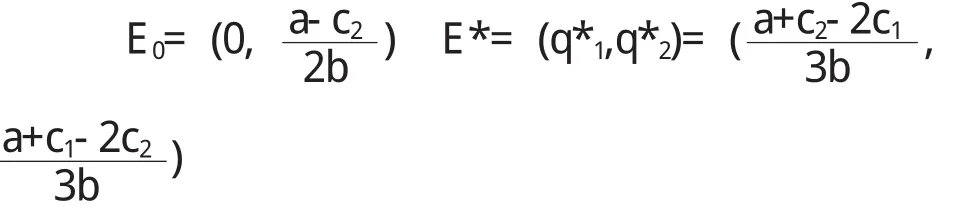

2 数值模拟


3 市场对初始条件的敏感性


4 结束语
