卫星数据广播分发系统中LT码的研究
2010-09-18朱宏鹏张更新李广侠
朱宏鹏,张更新,李广侠
(解放军理工大学 通信工程学院,江苏 南京 210007)
1 引言
卫星数据广播分发系统具有天然广播特性,能够实现各类信息的综合、分发和管理。由于卫星信道发生分组差错的概率较高,加上各接收机分处不同的地点,其工作环境和地球站技术指标可能各不相同,导致系统具有异构性。因此,必须采取一些措施来降低分组差错率、克服系统异构性,否则会严重制约卫星数据广播分发系统的应用。采用分组级前向纠错编码(FEC)技术,能够有效解决卫星数据广播分发系统中高分组差错率和信道特性异构性所带来的时延长、分组成功分发概率低、信道利用率低等问题[1]。
RSE码是一项传统的分组级FEC技术,其编译码时延大,系统资源消耗大,容忍的丢包率低,不适合大量用户的数据传输[2]。文献[3]提出了一类新的分组级FEC技术,即喷泉码,其主要包括LT码[4]和Raptor码[5]。该技术采用随机编码思想,编码码率动态可变,在有限数目的原始数据分组输入的情况下可以产生无限数目的编码数据分组,接收端在收到任意一组稍多于原始数据分组总数的编码分组后,就能正确恢复出所有的原始数据分组,而不管具体接收到的是哪些编码分组。喷泉码编译码时延小,且能够保证任意数量信道特性异构的用户可以在任意时刻接入系统并以很高的效率完成数据的接收[3],因此,已经被第三代蜂窝网络多媒体广播/多点传送服务(MBMS)和 DVB-H标准(手机电视标准)所采用[6]。
度分布算法是影响喷泉码中LT码性能的关键。目前LT码采用的是健壮孤立子度分布算法[4],其恢复出所有原始数据分组所需要编码分组的数目仍然偏大,且多次实验结果存在较大的波动。本文提出一种理论上可解但并不实用的最优度分布算法,并在此基础上给出一种实用的次优度分布算法。仿真结果表明,次优度分布算法的译码性能优于健壮孤立子度分布算法,采用基于次优度分布算法的改进型LT码对提高卫星数据广播分发系统的信道利用率大有裨益。
2 系统模型与协议框架
在卫星数据广播分发系统中,作为信息源的数据分发中心将信息通过同一条上行链路发送到卫星,然后由卫星转发给大量的接收机。由于采用同一条上行链路,各接收机具有相同的上行链路误码特性,但各接收机所处地点和工作环境不同,各自的下行链路具有不同的误码特性。图1给出了卫星数据广播分发系统的简化模型,其中,Pu为上行链路的分组出错概率,Pdm为第m个接收机下行链路的分组出错概率。
为了克服信道特性的异构性,降低分组出错概率,减少重发丢失的分组,提高系统的信道利用率,在分发系统的协议栈中加入分组级FEC层,使其位于网络层之上,用于保证上层协议的可靠工作,协议栈结构如图2所示。
在上述协议栈结构中,分组级 FEC层可以采用RSE码或喷泉码等,本文在此采用喷泉码中的LT码。
3 LT码编译码原理
对文中所用的参数作如下说明:原始数据长度为 N,分组长度为l,原始数据分组的数目为 k,k=[N/l],接收端参加译码的一共有 E 个编码分组,编码分组的度为d。
LT码编码过程如下。
1) 欲产生一个编码分组,则需要按照度分布函数随机选择一个度d。
2) 从所有的原始数据分组中等概随机地选取d个分组作为生成该编码分组的原始数据分组。
3) 将选取的d个原始数据分组进行异或运算,得出的结果便是编码分组的值。
4) 重复以上步骤可以源源不断地产生编码分组。
上面第2步在随机选取d个原始数据分组时,如果完全随机选择,为了在编码分组的报头信息中传送原始数据分组的位置信息,需要占用 dlbkbit的开销,其中,k为原始数据分组的数目。当k和d较大时,此项开销很大,在实际应用中并不可取,因此文献[7]给出了实用的有限随机LT码的构造方法,可大大节省报头开销。
下面介绍LT码的译码过程和度分布函数。
定义1LT译码过程:开始时k个原始数据分组均未被恢复。首先,释放E个编码分组中所有度数为1的分组,恢复出它们所对应的原始数据分组。已经被恢复出来但还未被处理的原始数据分组的集合构成预处理集。译码过程中每一步处理操作如下:从预处理集中选出一个原始数据分组,将该分组与E个编码分组中尚未被释放的且和它相关的所有分组进行异或运算,所有参加异或运算的编码分组度数减1,异或之后度数变为1的编码分组被释放,所对应的原始数据分组被恢复出来并加到预处理集当中。刚刚处理的原始数据分组从预处理集当中剔出,而处理之后新恢复的原始数据分组如果不在预处理集当中,则这些分组就会引起预处理集的增长,反之,则不会引起预处理集的增长。当预处理集为空时,即没有可以被处理的原始数据分组时,此过程结束。译码失败是指在所有的原始数据分组被恢复出来之前预处理集就已经变空。
定义 2度分布函数:对于所有的度 d,度分布函数ρ(d)是编码分组度数为d的概率。
定义3编码分组释放概率∶ q(i,L)表示度数为i的编码分组在还有L个原始数据分组未被处理时被释放的概率。
定理1编码分组释放概率如下:i和L为其他 (1)

定理1的证明参见文献[4]。
定义4编码分组总释放概率:r(i,L)表示在还有L个原始数据分组未被处理时度数为i的编码分组被选中并被释放的概率,即r(i,L)= ρ(i)q(i,L)。r(L)表示还有L个原始数据分组未被处理时一个编码分
定义5理想孤立子度分布函数:
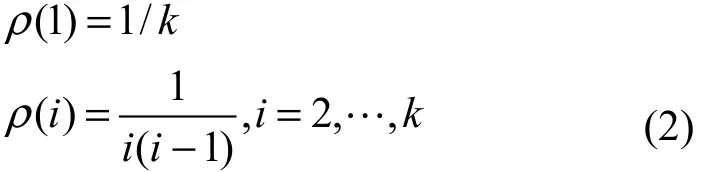
定理 2对于理想孤立子度分布函数,编码分组总释放概率,对于L=1, 2,…, k中所有的值都成立。
定理2的证明参见文献[4]。
采用理想孤立子度分布函数的 LT码每个编码分组在每一步被释放的概率为 1/k,当编码分组的数目E=k时,每一步平均释放一个编码分组,即每处理完预处理集中的一个原始数据分组后,刚释放的编码分组所对应的原始数据分组就会增加到预处理集当中,使预处理集的大小保持为 1,经过 k步处理后,k个编码分组都被释放,k个原始数据分组均被恢复。但上面的过程都是基于均值进行分析的,实际应用中会出现波动,常常在所有原始数据分组被恢复出之前预处理集就会变空。因此采用理想孤立子分布函数的LT码用k个编码分组恢复出k个原始数据分组的成功概率极小,正确恢复出所有的原始数据分组通常所需要的编码分组的数目要远远大于k。
针对理想孤立子分布函数存在的问题,文献[4]通过增加预处理集的初始大小来减小实际应用中译码失败的概率,并给出了健壮孤立子度分布函数。
定义6健壮孤立子度分布函数:设预处理集的初始大小为R+1,定义

把 τ(i)与理想孤立子度分布函数 ρ(i)相加并作归一化处理,就得到健壮孤立子度分布函数µ(i),即

基于健壮孤立子度分布函数的传统 LT码,其恢复出所有原始数据分组所需要编码分组的数目仍然偏大,且多次实验结果存在较大的波动。
4 改进型LT码
本节将对 LT码的度分布算法进行改进,提出基于实用的次优度分布算法的改进型LT码。
4.1 最优度分布算法
本节将对 LT码的译码过程进行分析,找出最优度分布算法。
预处理集的大小设为R+1,在还有L个原始数据分组未被处理时,为了保证预处理集的大小不变,在处理完第k-L个原始数据分组后,需要一个新的原始数据分组增加到预处理集中。一个被释放的编码分组所对应的原始数据分组不落在原来的预处理集中的概率为(L-R)/L,因此为了增加一个新的原始数据分组到预处理集中,平均需要释放L/(L-R)个编码分组。
设编码分组度数为i的概率是ρ(i),根据定义4,在还有L个原始数据分组未被处理时,一个编码分组被释放的概率为

假设一共有E个编码分组,则第k-L步处理后平均释放的编码分组的数目为

根据上面的分析,第k-L步处理平均需要释放L/(L-R)个编码分组,因此
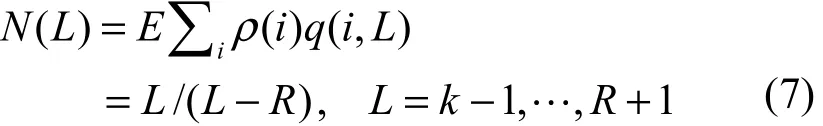
刚开始需要保证预处理集的大小为R+1,因此编码分组度数为1的概率

将式(1)和式(7)结合起来,再令 n(i)=Eρ(i),可以得到:
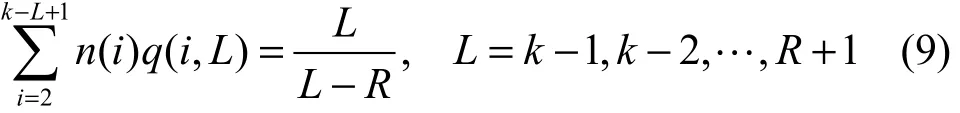
将式(9)用矩阵形式表示
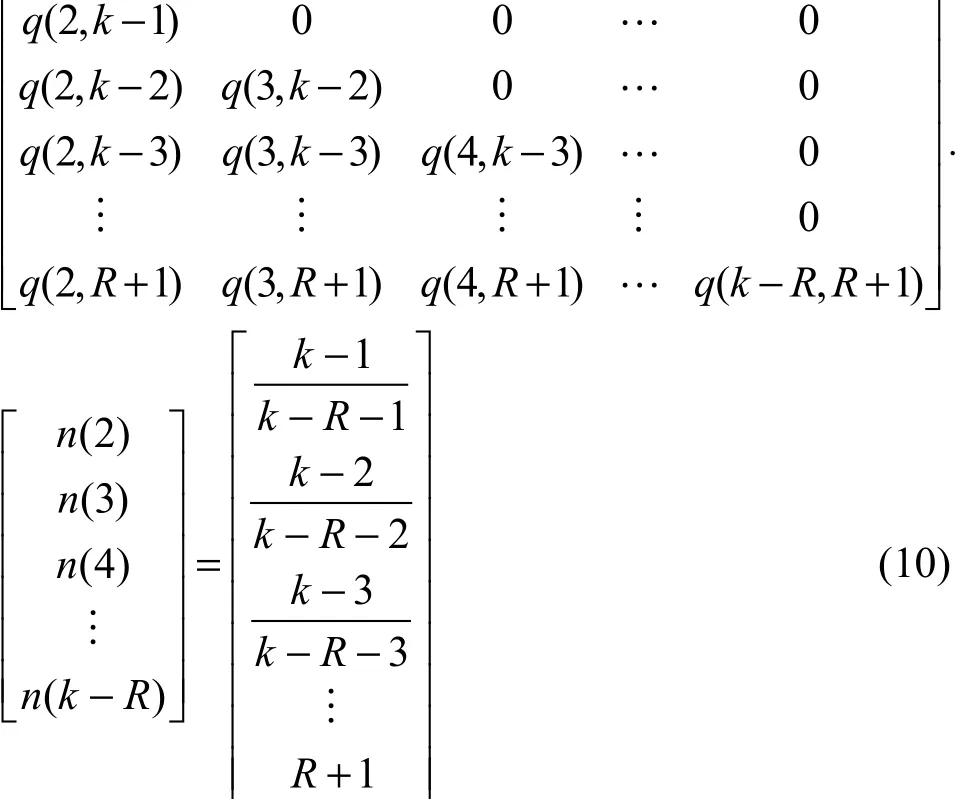
上面等式的系数矩阵可由式(1)求得,且其为下三角矩阵,从而可以求出n(i),i=2,3,…,k-R。
度数为1到k-R之间的所有编码分组的数目之和为E,即
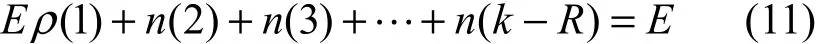
可以得出E的值。
因此由式(8)、式(10)和式(11)可以得出最优度分布函数:
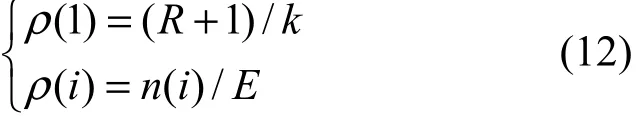
在实际应用中,当原始数据分组的数目k较大时,式(10)中系数矩阵对角线上大部分元素的值都非常小,系数矩阵的行列式近似为 0,矩阵呈现病态,基于运算能力的限制,常规方法无法求出变量n(i),因此最优度分布算法理论上可解,但不实用。
4.2 次优度分布算法
本节将在最优度分布算法的基础上提出实用的次优度分布算法。
译码过程中预处理集的大小仍设为R+1,在处理第k-L个原始数据分组时,为了保证预处理集的大小不变,平均需要释放 L/(L-R)个编码分组,即式(7)仍然成立。
由文献[4]中对理想孤立子分布函数的分析可知
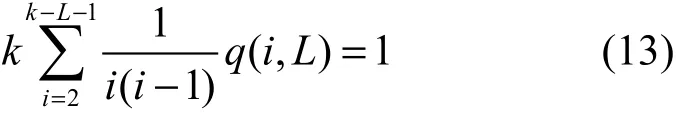
根据式(13),当还有L个原始数据分组未被处理时,若
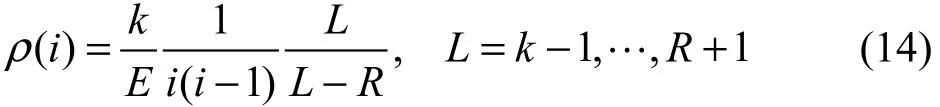
则式(7)成立。
式(14)存在的问题是在译码过程中随着L的变化,ρ(i)需要取不同的值,但在实际应用中对于整个编译码的设计,ρ(i)的值是固定的,因此对式(14)中不同的L得出的ρ(i)取平均得到
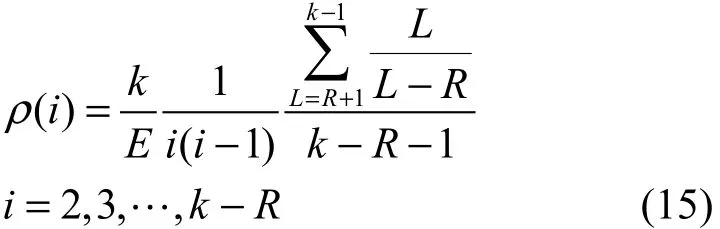
为了保证预处理集的初始大小为R+1,

在处理完第k-R个原始数据分组时,由于译码过程的随机效应,剩下的未被处理的R个原始数据分组并不一定都在预处理集中。在经典的小球扔盒子的模型[8]中,将小球以相等的概率扔到R个盒子中的任意一个盒子,最终为了保证每个盒子中都有小球的概率大于 1-δ,约需要 Rln(R/δ)个小球。为使剩下的 R个分组都能以大于 1-δ的概率恢复出来,令度数为k-R+1的编码分组的数目为Rln(R/δ)/(k-R+1),因此

所有度的概率之和为1,即

根据式(15)~式(18)可以求出所需编码分组的数目E。
综合式(15)~式(17),即可得到 LT码的次优度分布函数。

改进型 LT码则根据次优度分布算法决定每个编码分组的度,进而随机选取相应数量的原始数据分组进行编码。
5 性能仿真与分析
本文通过信道利用率来衡量改进型LT码对卫星数据广播分发系统分发性能的影响,并将其与基于健壮孤立子度分布函数的传统LT码、RSE码以及不采用分组级FEC技术时系统的性能进行比较。
定义7 信道利用率:信道利用率e表示原始数据分组数目k与为完成译码而发送的编码分组数目S的比值,即e=k/S。
本节在局域网环境下仿真卫星数据广播分发系统,利用局域网中的服务器充当分发系统的分发中心,5台客户机分别充当分发系统中的5台接收机。为了模拟信道特性异构的网络环境,5台接收机的分组出错概率分别设为0.05、0.1、0.15、0.2和0.25。原始数据选用 350Kbyte的文件,分组长度设为512byte。对于传统LT码和改进型LT码,预处理集的大小设定参见文献[9], R = a + b4k ,其中 a 、b的确定则根据对仿真结果的比较选择一组较优的值,在本文的仿真中a=2,b=8。对于RSE码,编码码率设为(5,10)。为了克服突发错的影响,先对所有码组中的 R SE编码分组进行交织编码然后发送。在不采用分组级 F EC技术时,同样为了克服突发错,将源文件分为多个文件块,块大小与采用 R SE码时码组大小相同,设为5个分组,然后对所有文件块中的原始数据分组进行交织编码,再发送出去。对采用改进型LT码、传统LT码、RSE码以及不采用分组级FEC技术4种情形下系统的信道利用率分别仿真200次,计算出200次仿真得出的信道利用率的均值,并以该参数作为指标来衡量系统的分发性能。
从图3的仿真结果可以看出,对于分组出错概率不同的5个接收机,分组出错概率越高,信道利用率越低。对于所有的接收机而言,信道利用率从高到低依次为改进型LT码、传统LT码、RSE码,不采用分组级FEC时性能最差。
分组级 FEC技术通过引入冗余分组和增强发送分组之间的相关性来提高系统的纠错能力,从而减小重发概率,提高系统的信道利用率。因此图 3中2种LT码和RSE码的性能要优于不采用分组级FEC时的性能。

图3 分组出错概率不同的接收机对应的信道利用率
改进型LT码的性能优于传统LT码,是因为传统LT码在分析译码过程时进行了较大程度的近似。在还有L个原始数据分组未被处理时,度数为 k/L的编码分组被释放的概率最大[10],因此在第k-L步处理中只对度数i=k/L的编码分组进行分析,再将得出的结果推广到所有的i;而改进型LT码采用的次优度分布函数基于最优度分布函数,在分析 LT码的译码过程时相对更加精确,因此性能更优。
下面分析2种LT码的性能均优于RSE码的原因。RSE码的编译码时延与码组大小的平方成正比,为了减小译码时延,码组不能设得很大,因此一个文件需要分为多个码组。在接收端,一部分码组正确译码,另一部分码组由于分组出错没能完成译码,需要继续接收编码分组,而已经完成译码的码组就会收到属于该码组的但对译码无用的分组,降低了信道利用率。LT码的编译码时延与码组大小呈近似线性关系,码组可以远远大于 RSE码的码组; LT码采用了随机编码的思想,接收端收到的每一个编码分组几乎都能提供有用的译码信息,接收端只要收到稍多于原始数据分组的编码分组就能正确恢复出所有的原始数据分组,因此系统的信道利用率更加接近于理论上的极限值。
接下来对不同分组长度对应的数据分发性能进行仿真。以分组出错概率为0.1的接收机为例,分组长度l分别设为256byte、512byte和1 024byte。每个仿真做200次,统计平均信道利用率。仿真结果如图4所示。

图4 不同分组长度对应的信道利用率
从仿真结果可以看出,对于同一个分发文件,当分组长度增加时,原始数据分组的数目就会减少,改进型LT码和传统LT码对应的信道利用率会随之降低,而采用RSE码和不采用分组级FEC技术时对应的信道利用率会随之增大,下面给出2种不同趋势的原因。当原始数据分组的数目减少时,采用随机编码思想的LT码随机性下降,随机产生的编码分组含有相同信息的概率就会增大,因此信道利用率会随分组长度的增加呈下降趋势。对于采用RSE码以及不采用分组级FEC技术而言,由于对源文件都采用了分块处理,当每个码组的分组数目固定时,原始数据分组数目的减少会导致码组数目的减少。当某个码组没有接收到足够多的分组而继续接收时,其他码组接收到的无用分组就会变少,因此信道利用率会随着分组长度的增加呈上升趋势。
最后,本文还比较了改进型LT码、传统LT码和RSE码的译码时间,仿真结果如图5所示。从图中可以看出,改进型LT码与传统LT码的译码时间相近,并远远小于RSE码。RSE码采用复杂的矩阵运算,编译码复杂度与码组中包含的分组数目的平方成正比,因此译码时间很长。改进型 LT码和传统LT码均是基于简单的异或运算,运算复杂度低,译码时间短,如本文仿真中2种LT码的译码时间都只有250ms左右。
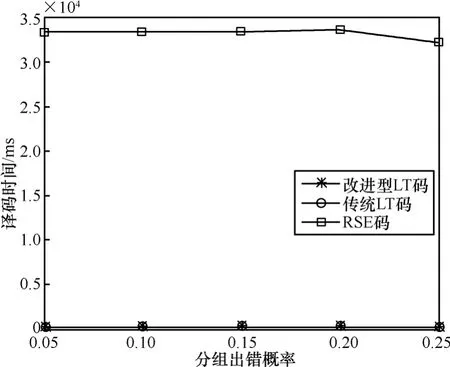
图5 3种分组级FEC的译码时间对比
6 结束语
分组级 FEC层能够在网络层上有效解决异构网络中存在的分组成功分发概率低、时延大、信道利用率低等问题。喷泉码中的 LT码是一项适合在分组级 FEC层上采用的技术,度分布算法是影响
LT码性能好坏的关键。本文通过研究,理论上可解但实际中不可用的 LT码最优度分布算法,提出了实用的次优度分布算法,并将基于次优度分布算法的改进型LT码应用于卫星数据广播分发系统,考察其对分发系统信道利用率的影响。仿真结果表明,本文提出的改进型 LT码译码复杂度低,将其应用于卫星数据广播分发系统,系统的信道利用率要优于传统LT码,且远远好于采用RSE码和不采用分组级FEC技术时的信道利用率。研究结果为基于LT码的Raptor码[5]的性能改进奠定了基础,对提高卫星数据广播分发系统的信道利用率具有重要的实用价值。
[1] 张更新, 张有志, 周坡. 卫星数据分发系统中的分组级FEC技术性能分析[J]. 电子与信息学报,2006, 28(1)∶112-115.ZHANG G X, ZHANG Y Z, ZHOU P. Performance analyse of packet level FEC in satellite data distribution system[J]. Journal of Electronics and Information Technology, 2006, 28(1)∶ 112-115.
Processing Advances in Wireless Communications (SPAWC)[C].Cesme, Turkey, 2012. 545-549.
[17] 张贤达. 矩阵分析与应用[M]. 北京∶ 清华大学出版社, 2004.ZHANG X D. Matrix Analysis and Application[M]. Beijing∶ Tsinghua University Press, 2004.
