基于最小聚类求解k-means问题算法

王守强，朱大铭

（1. 山东交通学院 信息工程系，山东 济南 250023；2. 山东大学 计算机科学与技术学院，山东 济南 250100）

1 引言

给定 d维空间中的点集P，k-means聚类问题要求在空间中选取k个中心点，使P中点与其距离最近的中心点的距离平方和最小。形式化描述为

实例：点集 P ∈Rd，正整数k∈Z+。

k-means问题相当于在d维空间中计算k个中心点，以中心点为核心将给定点集P划分为k个子集，优化目标为给定点到其所属子集中心点的距离平方和最小。该问题是NP-Hard问题[1]。其教科书算法为Lloyd给出的启发式算法[2,3]，Lloyd算法简单而容易实现，但运行结果依赖于初始值，算法无法保证一个确切的求解近似度。Kanungo[4]等采用局部搜索技术给出k-means问题（9+ε）近似度算法。在执行算法前需要对点集空间结构进行划分求得一个候选中心点集[5]，候选中心点集的求解十分复杂，算法显得不够实用。Song等[6]进一步证明，如果将给定点集P作为中心点的候选点集，对候选点集执行局部搜索，可使算法的近似度达到O(1)。2004年Kumar[7]等人给出求解k-means问题的(1+ε)随机近似算法，算法的时间复杂度为

2) 对于m最小聚类问题，改进了Kumar提出的 k-means问题的(1+ε)随机近似算法，将 Kumar给出算法的时间复杂度由 O ( 2(k/ε)O(1)dn)改进为证明改进算法求到(1+ε)近似解的成功概率至少为如果该算法运行次，则以接近于 1的概率求到该问题的(1+ε)近似解。

3) 设计出求解k-means问题的局部搜索随机算法。从k个初始中心点的选取以及生成候选中心点集2个方面分别对Song的局部搜索算法提出新的随机策略。Song局部搜索算法的时间复杂度为本文算法的时间复杂度为O(nk3dln(k)2)/α)。实验结果表明：新算法所求解的精度和算法的运算时间均优于 Song给出的局部搜索算法。

2 符号标记与基本结论

定义 2对于点集 P的 m最小聚类问题，称α=km/|P|为该问题的最小聚类参数。

定义3设是d维空间中的k个点，若存在 l个实数满足：

d对于 d维空间中某点 x ∈ R ，如果成立，则称 x为的凸组合点。

引理1[8]点集P的质心点为P的1-means问题最优解的中心点。

Inaba等[7]指出在欧氏空间中，只需从P中随机选取部分点，计算取样点的质心点，则该质心点以较大的概率成为P的 ε 近似质心点。该定理描述如下。

引理2[7]给定点集P，从P中均匀地随机选取m个点，设S为取样点的集合，m=|S|， c(S)为S的质心点。存在δ (0＜δ＜1)，使下述不等式成立的概率至少为1-δ。

引理3[8]给定点集P，对于任一个点x ∈ Rd，

3 基于取样技术k-means近似算法

3.1 近似度期望值为2的算法

记 ∆k2(P )为给定实例点集 P的最优解的解值。在给出该算法之前，首先探讨当中心点集包含每个最优子集 Pi(1≤i≤k)中的一个点时，算法近似度的期望值。

定理 1设 P所对应的最优聚类划分子集为如果从每个 Pi中均匀地随机选取一个点ci，以这k个点作为中心点求到的解值记为∆，则

证明设 P的最优解所对应的中心点为从每个 Pi中均匀地随机选取一个点 ci，由所有 ci构成中心点集合记为不失一般性，假设 ci∈Pi，根据已知条件，Pi中任一点被选作中心点 ci的概率为针对点 x ∈Pi,定义{distance(x,ci)}，D(x)实际表示为点x与集合 C - { ci}中最近点的距离，则由此可得：

(根据引理3)

给定正整数m，如果P为m最小聚类问题。下面证明只需从P中随机选取一个样本点集S，则S以较高的概率满足它包含每个最优子集 Pi中至少一个点，即

定理2如果从P中均匀地随机选取k ln(2k)个点，记取样点集为S，那么对于所有P，αi均成立的概率至少为1，即∀iPr[|S∩P|2i

证明不失一般性，设|记定义则 nis的期望值根据Chernoff Bounds不等式得：

其中，0＜λ＜1。定义事件Ai为满足足 nis小于λ|S |nni的事件，则：

对每个最优子集Pi，如果均成立，枚举S中所有k个点的子集，则至少存在一个子集满足：k个点分别来自于最优子集 P1,P2,… ,Pk中的一个点。以这k个点作为中心点，根据定理1知，所求解的近似性能比的期望值至多为 2。据此，给出下述算法。

算法1k-means问题近似算法

输入：点集P，参数α。

2) 从S中任取k个点，以这k个点作为中心点，对P进行一次划分，计算划分后的值∆。

3) 重复2)的操作，枚举所有可能k个点，选择∆ 最小的值所对应的k个中心点作为算法最终解。

4) 返回所求的中心点。

定理3算法1至少以1/2的概率求到近似度期望值为2的解。

证明根据定理1及定理2，该定理结论显然成立。

算法在求得k个中心点时，通过枚举取样点集中所有k个点的子集找出最小解。枚举子集的个数为 C|kS|，由于将S值代入该式可得枚举子集个数为由于每次将实例点集P中的点分配给k个中心点时，时间复杂度为 O(nkd)。因此，算法 1的时间复杂度为

3.2 k-means聚类(1+ε)近似算法

定理4对满足m最小聚类问题实例点集P，如果从P中均匀地随机选取8 k ln(4k)个点，记取样εα点集为S，则S包含每个最优子集Pi中至少2/ε个点的概率大于等于3/4。

证明证明过程类似于定理 2。记 ni=|Pi|，定义则 nis的期望值根据Chernoff Bounds不等式得：

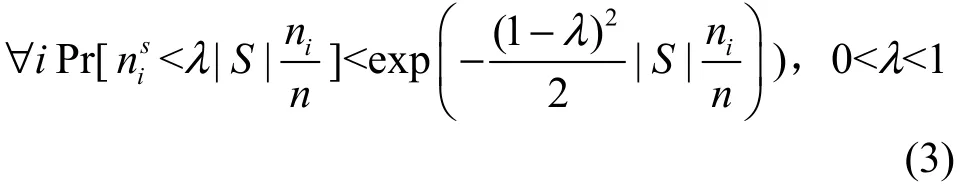
定义事件Ai为 nis小于λ|S |nni的事件，则：

由于|Pk|≥m，根据最小聚类参数定义α=km/|P|可得成立。

引理4给定点集P，设均属于P中同一个最优子集Pi中的点，如果x∈P并且 x是由所组成凸组合的点，则x∈Pi

证明由于 x是属于中凸组合内的点，根据凸组合定义，存在l个大于等于0的数值满 足 ：其 中设 ci为 Pi的质心点，则：

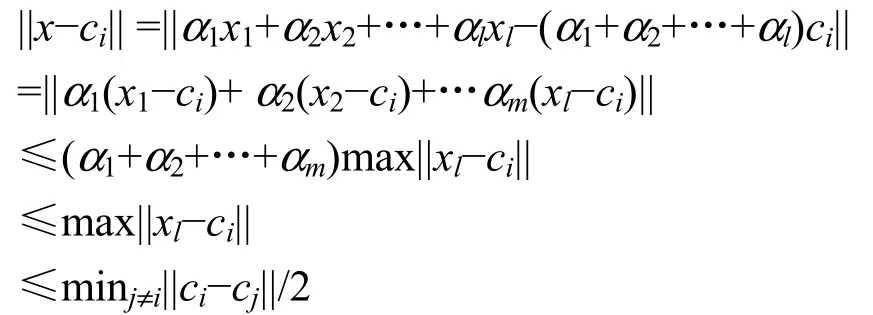
算法2k-means问题(1+ε)近似算法

输入：点集P，参数ε，每个子集最少聚类个数m。

1) 计算参数α＝(mk)/|P|，置C=φ。

3) 调用函数 Cost=Online-k-means(S, C, ε)。

4) 返回代价Cost及集合C。

函数 Online-k-means(·)的实现采用递归方法，从i＝1开始，首先从S中枚举所有2/ε个点的子集，则至少存在一个子集 Si′满足 Si′⊆Si，由 Si′求出 Si′′并进一步计算 Si′∪ Si′的质心点 ci′，然后从S中删除属于集合 Si′∪ Si′中的所有点。删除 Si′∪ Si′中的所有点的目的在于当求解下一个子集时，可以减少枚举子集的个数，从而提高算法的运行效率。函数的实现过程描述如下。

函数 Online-k-means(S, C, ε)

输入：样本点集S，已求中心点集C，参数ε 值。

1) If |C|=k then

2) 以C作为中心点，计算解值Sum。

3) if Sum＜MinCost then MinCost=Sum，保存C和MinCost。

4) If |C|＜k and |S|＜2/ε 返回。

5) Repeat。

6) 从S中取2/ε个点,设点的集合为S′。

7) 从S-S′中找出满足S′凸组合中的点，设点集为 S ''。

9) Online-k-means(S,C, ε)。

10) Until 穷举完毕S中所有2/ε个点的子集。

11) 返回MinCost的解值。

引理 5如果对每个最优子集 Pi，均成立，则函数 Online-k-means(·)能够从 S中求出一个子集 Si′，满足成立。

证明记由上述第 6)步知，算法是从 S中枚举所有 2/ε个点，则枚举子集中必存在一个子集S′属于Si。上述第7）步求出S中满足S′的凸组合的点集 S′，根据引理 4，，因此并且成立。

引理 6对每个最优子集 Pi，如果成立，则函数 Online-k-means(·)求出 k-means问题(1+ε)近似解的成功概率不小于(1/2)k。

证明根据引理5，对每个最优子集Pi，函数Online-k-means(·)从 S中求出一个子集 Si′，Si′满足成立。以 Si′的质心点作为 Pi的中心点，根据引理2，该质心点至少以1/2的概率满足Pi的 1-means问题的(1+ε)近似解。因此，算法求解 k-means问题(1+ε)近似解的成功概率至少为(1/2)k。

定理5对于满足m最小聚类的点集P，算法2至少以2的概率求出该问题的(1+ε)近似算法，算

2k+2法的时间复杂度为

证明根据定理4，对任意最优子集成立的概率不小于 3/4。当条件成立时，由引理 6知，函数 Online-k-means(·)求解k-means问题(1+ε)近似解的成功概率至少为(1/2)k。因此，算法2的成功概率为

记 r=2/ε，T(|S|)代表求函数 Online-k-means(·)中以 S作为实例点集的枚举个数，则：由此可得T(|S|)至多为

将|S|及r值代入上式可得：枚举所有可能k个中心点的子集个数至多为因此整个算法的时间复杂度为

3.3 局部搜索随机算法

基于文献[6]的局部搜索算法，本文提出k-means问题的局部搜索的随机算法，其随机策略主要体现如下。

1) 文献[6]候选中心点集选自给定实例点集P，新的随机算法则以 P的一个取样子集作为候选中心点集，S满足以较高的概率包含每个最优子集至少一个点。

2) 在 k个初始中心点的选取方面。文献[6]是从候选中心点集中任取k个点，新的随机算法则采用非均匀地随机选取策略从P中选取k个点，使得这k个点尽可能地分属于k个不同最优子集中的点。

初始中心点选取算法实现描述如下。

算法3k个初始中心点选取算法

输入：点集P

1) 从P中随机选取2个点 x1、 x2，选择概率

2) While 选取点数≤k。

3) 从P中随机选取一点xi(i≥3)，选取概率为

4) End While。

5) 返回选取点{x1,…, xk}。

算法3首先从P中随机选取2个点 S = { x1,x2}，遵循两点距离越大，被选取概率越大的原则。再依次随机选取点 x3,… ,xk，选取第i(i＞2)个点时，遵循一个点与已选择的点距离平方和越大，则该点被选取概率越大的原则。因此算法规定第一次选择2个点{x1,x2}的概率表达式为设规定选择第i个点xi的概率表达式为算法4k-means局部搜索随机算法

输入：点集P，最小聚类参数α。

3) Repeat。

4) 以C为中心点，对S作一次划分，划分子集为{S1,S2,…,Sk}。

5) For i=1 to k。

6) 对于Si中每一个点x，以C′为中心点,计算给定点集P的k-means解值∆′,如果∆′＜∆,置

7) Next i。

9) 返回C以及解值∆。

与文献[6]局部搜索算法相比，选取k个初始中心点时，算法4中的第2)步不是从给定实例点集P中任取k个点，而是调用算法3从P中非均匀地随机选取k个初始中心点。算法4中的第3)～8)步局部搜索时以取样子集S作为候选中心点集。根据定理2，该取样子集能够较好地代表P。在执行中心点交换时，取样子集能够减少交换次数，从而达到降底算法时间复杂度的目的。

根据算法4第6)步，算法每次迭代时，所求P的值下降(1-ε/k)倍。记∆k2(P)为给定实例点集 P的最优解值，∆2(P,C)为算法所求最终解值，∆2(P,C0)为算法初始中心点所对应的值，算法的迭代次数记为t。则：

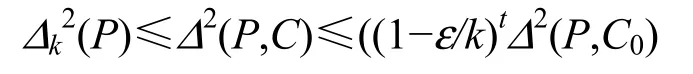
由此可得：算法迭代次数

4 实验结果

本文选用 Iris、RuspIni、Spath Postal Zone Data、Cloud 和SPAM 数据集测试本文相关算法。选用数据集 Iris、RuspIni、Spath Postal Zone Data来验证算法1的运算结果；选用UCI中2个高维数据集Cloud以及SPAM测试局部搜索随机算法的运算性能。表1列出5个数据集的基本属性。

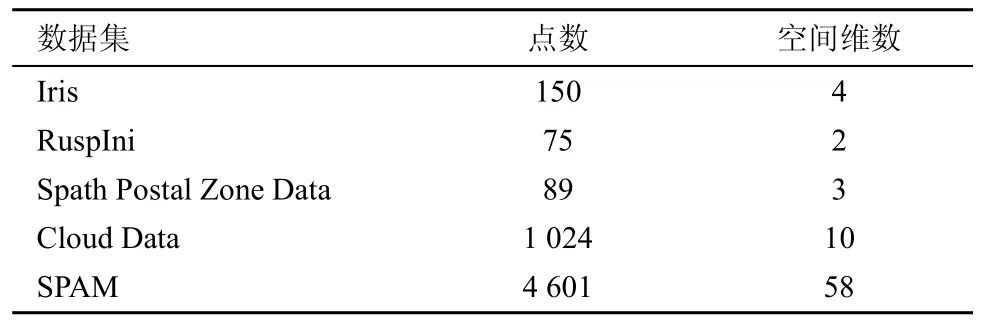
表1 选用数据集说明

4.1 近似度算法实验

根据算法 1，在执行算法前，需要给出算法的最小聚类参数α。受篇幅所限、仅给出α=0.5作为参数值，对不同的k值进行实验结果。表2中最优值一列来自于文献[10～12]。由于算法的随机性，表2中实验结果取自算法运算 20次后所求解值的最小值，实验结果参见表2。

表2 算法1实验结果(α＝0.5)

在表2中，近似度一列值等于实验结果与最优值的比值。由表2近似度一列可知：本文实验所得到的算法近似度均小于2。通过表2实验结果可以看出：对随机取样点集S，枚举S中所有可能k个点子集作为中心点，则以较高概率获得近似度期望值为2的解。1的常数，因此，迭代此数可简化为O(kln(k))。由算法4的第7)步知，每次迭代时，需要涉及|S|个中心点交换；每次交换后，算法重新计算k-means解值的时间复杂度为O(nkd)。所以，整个算法4的时

4.2 改进局部搜索算法实验

为检验改进后局部搜索算法性能，本文将数据集Cloud以及SPAM分别应用在文献[6]局部搜索算法以及本文算法4上进行测试。表3给出2种算法的实验结果，由于初始中心点选取随机性，将程序执行20次。表2中运算值所对应的两列是指两算法运算20次后所求的最小值，而表2中运算时间所对应的2列值则指程序20次运算后的平均时间。

为便于比较和描述，表中 2运算值=算法实际运行结果/点集个数。

表3 局部搜索算法实验结果

相对于文献[6]，定义算法 4的改进值=[1-(算法4)/(文献[6]算法)]×100%。对于Cloud数据集，当k=10、25、50时，算法2第2）步的运算时间分别改进了96.75%、93.32%以及89.21%，因此算法时间得到显著提高。除运算时间外，局部搜索随机算法的运算值也均小于文献[6]的算法。对于SPAM数据，当 k=10、25、50时，算法所求的解值分别改进了51.91%、87.38%和91.63%，而算法的运算时间则分别改进了98.98%、97.98%以及96.39%。由表3可以看出，针对给定的实例点集P，采用局部搜索随机算法，无论是算法所求值的精度还是算法的运算时间均优于文[6]所给出的算法。

5 结束语

本文分析了基于最小聚类k-means问题的随机近似算法，利用取样技术，给出了该问题近似度期望值为2的随机算法。同时探讨了该子问题的(1+ε)近似算法的求解方案，将 Kumar所给出的(1+ε)近似方案的时间复杂度进行了改进，并分析了算法的成功概率。利用取样技术，本文设计局部搜索随机算法。最后，选取了部分实验数据，对算法近似度以及局部搜索随机算法进行了验证。但本文还有几个问题需要进行探讨。1) 本文近似算法是通过枚举样本点集中部分点的求到的，显然算法的时间复杂度高，能否不需要进行组合，而是通过某种策略直解在取样子集中找出满足给定条件的某些点？2) 该算法能否进一步提高成功概率？3) 如何找出k个初始中心点，使得这k个点以较高的概率分别来自于k个不同最优子集中的一个点。

[1] DRINEAS P, FRIEZE A, KANNAN R, et al. Clustering large graphs via the singular value decomposition[J]. Machine Learning, 2004,56(1-3)∶9-33.

[2] MACQUEEN J B. Some methods for classification and analysis of multivariate observations[A]. Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability[C]. California, USA,1967. 281-297.

[3] LLOYD S P. Least squares quantization in PCM [J]. IEEE Transactions on Information Theory, 1982, 28(2)∶129-137.

[4] KANUNGO T, MOUNT D M, NETANYAHU N, et al. A local search approximation algorithm for k-means clustering[J]. Computational Geometry, 2004, 28∶ 89-112.

[5] MATOUSEK J. On approximate geometric k-clustering[J]. Discrete and Computational Geometry, 2000, 24∶ 61-84.

[6] SONG M J, RAJASEKARAN S. Fast k-means algorithms with constant approximation[A]. Proceedings of the 16th Annual International Symposium on Algorithms and Computation[C]. Sanya, Hainan,China, 2005,1029-1038.

[7] INABA M, KAOTH N, IMAI H. Application of weighted voronoi diagrams and randomization to variance-based k-clustering(extended abstract)[A]. Proceedings of the tenth annual symposium on Computational Geometry[C]. Stony Brook, New York, USA, 1994. 332-339.

[8] KUMAR A, SABHARWAL Y, SEN S. A sample linear time (1+ε)algorithm for k-means clustering in any dimensions[A]. Proceedings of the 45th IEEE Symposium on the Foundations of Computer science[C].Washington, DC, USA, 2004. 454-462.

[9] MOTAWANI R, RAGHAVAN P. Randomized Algorithms[M]. Cambridge University Press, Cambridge, UK, 1995.

[10] RUSPINI E H. Numerical methods for fuzzy clustering[J]. Inform Science,1970, 2(3)∶319-350.

[11] SPAETH H. Cluster Analysis Algorithms for Data Reduction and Classification of Objects[M]. John Wiley & Sones, 1980.

[12] PENG J M, XIA Y. A New Theoretical Framework for k-Means-Type Clustering[R]. McMaster University, Advanced Optimization Laboratory, Tech Rep∶ ADVOL2004/06, 2004.