基于稳定性的FAST TCP参数γ调整

梁伟，张顺颐，宁向延，徐苏磊

（1. 南京邮电大学 信息网络技术研究所，江苏 南京 210003；2. 常熟理工学院 计算机科学与工程学院，江苏 常熟 215500）

1 引言

关于拥塞控制的研究工作当中，除了平稳状态性能分析，另一个主要就是拥塞控制算法的动态性能分析。尤其是要考虑不计反馈时延时的稳定性，以确保系统工作状态的确是趋于平衡的[1]。FAST TCP是在Vegas基础上采用反馈时延作为拥塞度量的改进方案，目的是解决高速大时延环境下传统算法带宽利用率不高的问题[2]。在高速网络环境下，带宽利用率可达90%以上，这一点是其他算法所无法比拟的。FAST根据距离平衡点位置的远近非线性地调整窗口大小变化的快慢，以此提高窗口的响应速度和减缓窗口的波动幅度，使得数据流始终处在最佳传输状态。直到最近2年才出现了对FAST稳定性能的实验探索和理论研究，在FAST TCP中参数γ是数据源控制强度，对网络性能有显著影响，而其设置范围的研究工作还远远不够。文献[3～6]提到相关的工作。在文献[7]中，对影响稳定的微观因素做了探讨，分析了2个RTT有差别的FAST数据流共享一条瓶颈链路时的稳定情况。文献[8]采用离散时间链路模型，推导了FAST的局域渐趋稳定的条件。文献[9]提到了一个数据源在一条瓶颈链路传输时，FAST的参数α、γ对稳定性的影响，有待于进一步分析多个数据源共享一条瓶颈链路的稳定情况。文献[10]应用Lyapunov函数分析了稳定条件，也是局限于一个FAST数据流传输的情况。在文献[11]中，参数 γ的值限定在(0,1]，在文献[12]中推荐γ设为0.5，在文献[13]中，γ的条件分析不够全面不够深入。

针对以上不足，本文对FAST TCP的稳定性进行深入探讨，目的是得出参数γ的边界条件。本文从分析稳态流量FAST负反馈模型来解决这个问题的，具体分析了1个数据流，2个数据流在一条瓶颈链路上传输时，网络的FAST参数γ的设置是如何影响稳定的。本文也对于一条瓶颈的链路上传输无数条数据流的情况作出了证明。

2 数学模型

2.1 网络流量模型

考虑在一条容量为C的瓶颈链路上有多条TCP数据流进行传输，如图1所示。各TCP流依次记为在本文中用p表示链路的排队时延，wn表示数据流 n的拥塞窗口大小， xn表示排队队列中数据源n的数据到达率，dn表示数据流n的链路传播时延，τn表示数据流n的往返时延RTT，其中它们均为时间t的函数，不带t加小括号的时候表示该变量平衡状态的值。设τnf为前一段链路传播时延，即从数据源n到瓶颈链路的传播时延。相应地，τb( t )为数据分组到达瓶颈链路后到

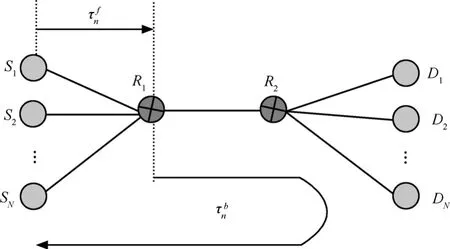
图1 TCP连接拓扑

n

研究表明基于窗口的拥塞控制假定发送速率与窗口大小除以往返时延成比例，把排队队列看成一个简单的积分器，对链路上大于链路容量的传输速率进行积分，于是有积分链路模型[14]：

2.2 FAST模型和网络

FAST TCP依据数据分组的排队时延 pn(t -τ)来设置拥塞窗口，它的发送速率是通过拥塞窗口机制来调整的，每个发送源根据下式的离散时间更新窗口大小[15]：

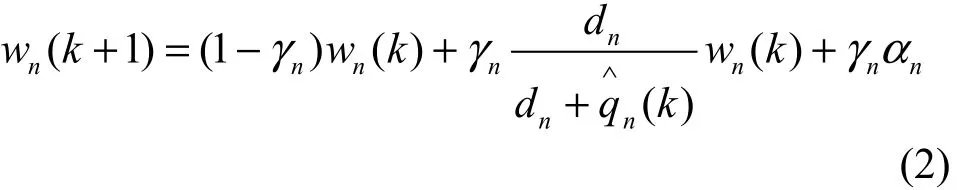
其中，αn∈Z+，αi是数据分组中的度量常数。γn为步长大小，是协议参数。窗口大小在每一个RTT之后执行更新一次。排队时延 qn(k)是由数据发送端

∧估计出的，第 k次的估计表示为 qn(k )。窗口算法是以RTT为基础进行，而估计值是以数据分组经历的时间为基础估算的。

3 稳定分析

3.1 二阶稳定分析

式(1)和式(2)的连续时间形式拉普拉斯变换为

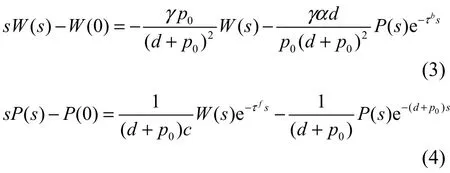
消去 ()Ps得：

运用padé二阶近似得传递函数的特征多项式为

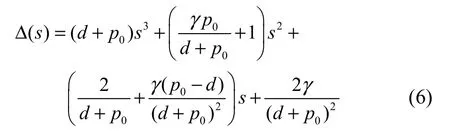
由以上2式，代入FAST TCP通常设置α、c和d的范围，可得稳定范围的上界约为1.55。为了得到工程应用上所许可的参数设置范围，下面对系统进行一阶近似来求系统稳定γ的设置范围。

3.2 一阶稳定性分析

瓶颈链路除了传输TCP流之外，也传输非窗口控制TCP流量，如UDP流量。令 xc(t)∈ [0 ,c]为非TCP流量大小，则TCP流量可以获得的链路带宽为c - xc(t)。根据来自于观察经验流量模型，窗口大小和链路缓存之间的关系可以表示为稳态链路模型[16]：

采用欧拉一阶微分近似，式(2)的连续时间形式的拉普拉斯变换式为[17]

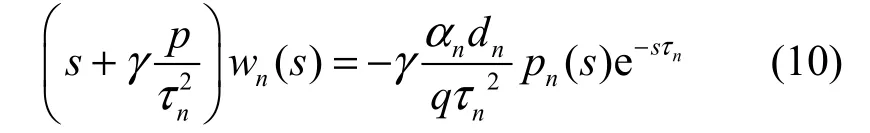
多个数据源共享一条瓶颈链路的窗口拥塞控制系统开环传递函数为

联立式(10)和式(9)的拉普拉斯变换式可以建立基于稳态链路模型的一个负反馈系统，开环传递函数具有式(11)的形式，其中这里

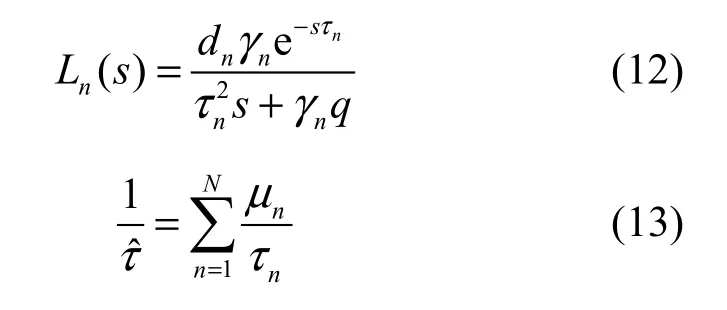
由此得到稳态链路的开环传递函数：

当 q → 0 时，每一项 Ln(s)都会增大，整个环路的传递函数的模会增大，系统的稳定性会下降，所以集中讨论 q → 0 的情况。这时稳态链路的开环传递函数式(14)变为

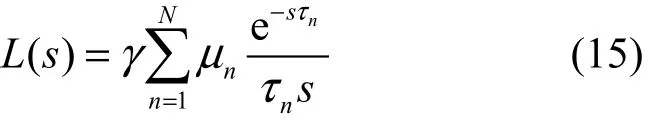
以下利用式(15)对系统稳定性进行分析。

3.2.1 1个FAST流在瓶颈链路上传输的情况

当N=1时，只有1个数据流，则1μ=，式(15)变为

在频域内考察式(16)系统的稳定性，以jω代替s，绘制ω由0→∞奈奎斯特曲线。根据奈奎斯特稳定性判据，如果曲线自下而上顺时针穿越区间( ,1)-∞- 的次数为0，则系统是稳定的。式(16)系统的频率特性为

3.2.2 2个FAST流在瓶颈链路上传输的情况

设2个FAST流的往返时延有关系式τ2=ητ1，其中，η表示2个数据流往返时延差别系数，取值范围为(1,+ ∞ )。式(15)变为

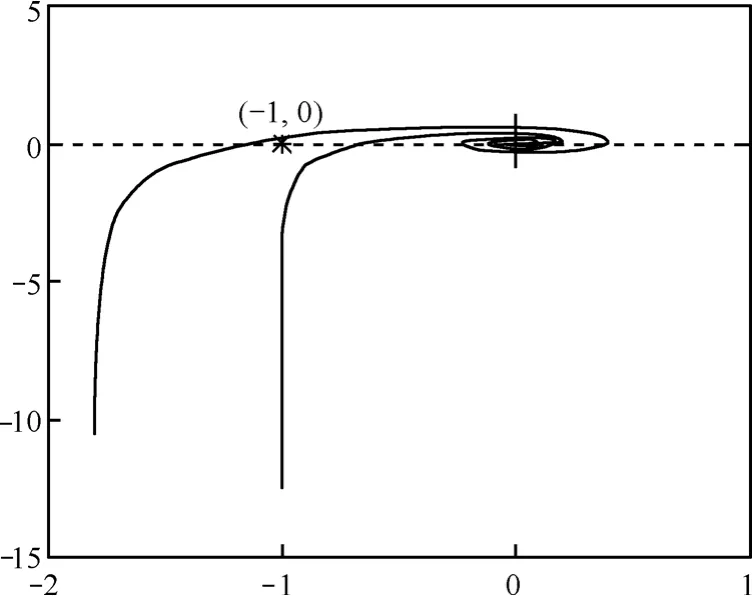
图2 时系统的Nyquist曲线

图3 2个FAST流不同RTT情况下γ的稳定边界

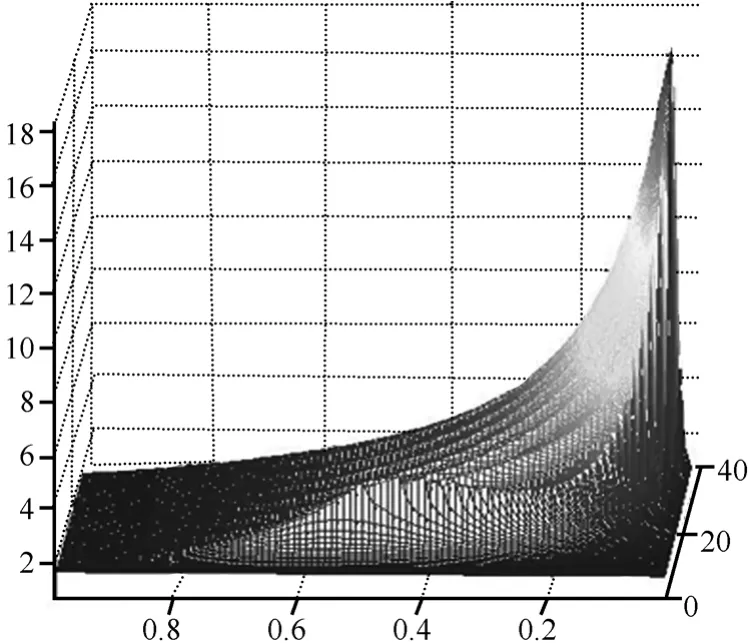
图4 当η和μ变化时，γ使系统稳定的取值

3.2.3 N=∞个FAST流在瓶颈链路上传输的情况

在实际的网络中，链路上有很多数据流同时传输。求出这种情况下稳定边界条件的统计平均是有意义的。考虑很多个数据流的RTT呈均匀分布的情况，即令其中τ0为所有数据流中RTT最小值，τ为最大值，其最大可以为无穷大。

这时式(15)稳定条件可以表示为：在条件

定理 如果

在式(18)描述的系统中，如果取η在区间(1,)+∞变化，1μ在(0,1)区间变化，可求出γ的稳定边界如三维图4所示。图中的曲面是γ值的稳定边界，γ取值在曲面上方时，系统不稳定，γ取值在曲面下方时，系统是稳定的。观察γ的极小值点，可以看出1μ趋于0或者趋于1时，这时实际上退化到了1个FAST流传输的情况，γ的稳定边界最小，1μ在0和1之间γ的稳定边界都较大。这就是说，2个FAST流传输时γ的稳定边界要大于1个FAST流传输的情况。

则在式(20)条件下，式(22)所确定的系统稳定。

证明设 H (ω)为复平面过点 - 1 + j0，斜率为的直线以下的半个平面如图 5所示，如果Nyquist曲线在这个平面以下，则系统是稳定的。这个平面可以表示为

图5 过点，斜率为的直线以下的半个平面

如果式(22)所确定的 L (s)满足 L (jω)∈ H(ω)，则系统是稳定的。

L(jω)∈ H(ω)等价于

令s=jω，将式(22)代入式(25)，并考虑到

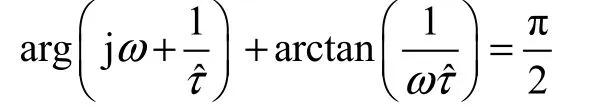
即当

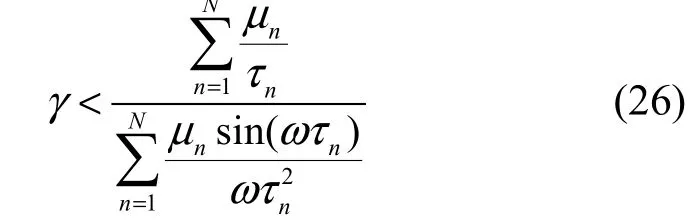
时，有 L (jω)∈ H(ω)。

当有无穷多个数据源N→∞时，式(26)变为

令θωτ=，由于有式(20)的条件，并假定总体上所有数据流的往返时延RTT服从均匀分布：

可得

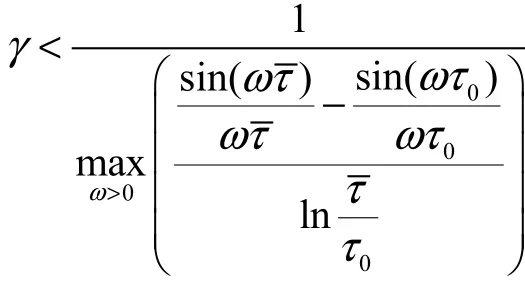
因为 L (jω)∈ H(ω)，根据Nyquist准则系统收敛，定理得证。

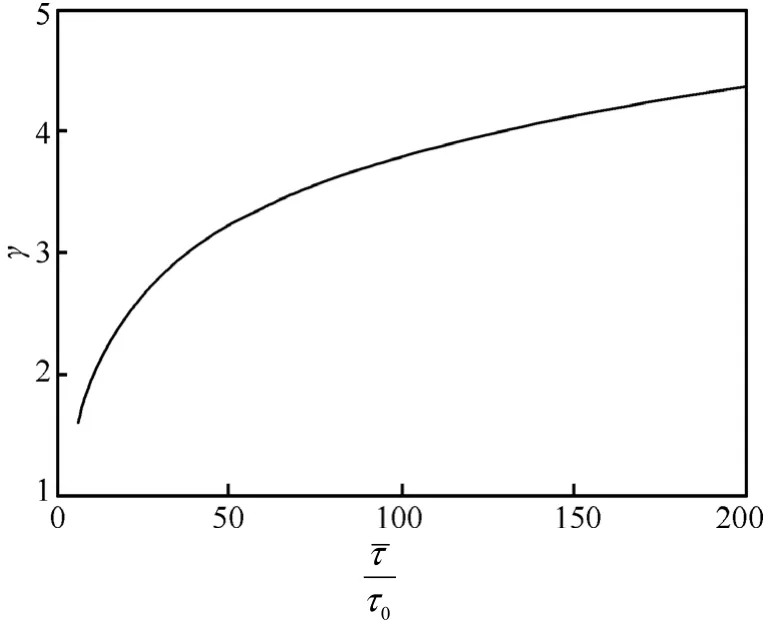
图6 定理中不等式(23)所确定的γ的曲线

4 仿真

FAST的ns2仿真软件在网站[18]上可以下载，设计实验仿真场景来验证参数γ对FAST 数据流传输稳定性的影响。多条FAST TCP数据流在一条容量为40Mbit/s的瓶颈链路上进行数据传输如图1所示，传输的数据分组大小为 1 000byte，传输延时d= 2 0ms ，瓶颈链路的传播时延为 4 ms，α=50packet。在1～500之间随机选择FAST数据流的个数进行传输，传播时延在400～700ms之间均匀分布。研究γ稳定界限的最小上界，发现当设置 γ=1.55，γ=1.63或γ=1.75时，排队队列的变化如图7(a)，图7(b)和图7(c)所示。图7(a)表明当γ=1.55时，排队队列依然稳定，图7(b)表明当γ=1.63时，排队队列开始出现波动，而图7(c)表明当γ=1.75时，排队队列的波动很大了。这说明得出的参数γ的设置选择范围与实验结果非常吻合。

图7 不同γ时的排队队列

5 结束语

本文根据稳态链路模型和积分链路模型对FAST TCP算法在复频域建立了负反馈控制系统，深入地分析了在一条瓶颈链路上FAST流的传输情况。对系统传递函数进行了二阶定性稳定分析，对1个FAST流、2个以及无穷多个数据源的情况下参数γ稳定边界条件进行了分析，在1个数据流时，γ= 1 . 57。随着传输的数据流的增多，参数γ的稳定边界增大，系统稳定将趋于宽松，稳定取值将大大高于1.57，接着ns2仿真证实了所得结论。所得结论以控制理论作为依据，仿真结果与本文的理论研究符合很好。本文的研究成果有助于FAST TCP的实际应用，使得参数γ的设置选择范围有了明确的理论指导方针。在将来大规模地实际应用 FAST TCP情况下，对采用本文建议的参数γ的效果可以做进一步研究。

[1] BELHAJ S. VFAST TCP∶ an improvement of FAST TCP[A]. Proc Tenth International Conference on Computer Modeling and Simulation[C]. 2008.88-93.

[2] CHEN M, FAN X. Normalized queueing delay∶ congestion control jointly utilizing delay and marking[J]. IEEE/ACM Transactions on Networking, 2009,17(2)∶618-631.

[3] ZHANG H, PENG L, FAN B, et al. Stability of FAST TCP in single-link multi-source network[A]. Proc 2009 World Congress on Computer Science and Information Engineering[C]. 2009. 369-373.

[4] BAIOCCHI A, VACIRCA F. TCP fluid modeling with a variable capacity bottleneck link[A]. Proc IEEE INFOCOM [C]. 2007. 1046-1054.

[5] TAN L, ZHANG W, YUAN C. On parameter tuning for FAST TCP[J].IEEE Commun Letters, 2007, 11(5)∶ 458-460.

[6] WANG J, WEI D X, LOW S H. Modeling and stability of FAST TCP[A]. INFOCOM 2005.24th Annual Joint Conference of the IEEE Computer and Communications Societies[C]. 2005.938-948.

[7] JACOBSSON K, HJALMARSSON H, MOLLER N. ACK-clock dynamics in network congestion control—an inner feedback loop with implications on i nelastic flow impact[A]. Proceedings of IEEE Conference on Decision and Control[C]. San Diego, USA, 2006.1882-1887.

[8] JACOBSSON K, ANDREW L L H, TANG A, et al. ACK-clocking dynamics∶ modeling the interaction between windows and the net-work[A]. Proc IEEE Infocom[C]. 2008. 2146-2151.

[9] WEI D, JIN C, LOW S H, et al. FAST TCP∶ motivation, architecture,algorithms, performance[J]. IEEE/ACM Trans Networking, 2006,14(6)∶ 1246-1259.

[10] ZHAO F, ZHOU J, LU N. Stability analysis of FAST TCP based on lyapunov function[A]. Proc 7th Word Congress on Intelligent Control and Automation[C]. 2008.2136-2140.

[11] WANG J, TANG A, LOW S H. Local stability of FAST TCP[A].Proceedings of IEEE Conference on Decision and Control[C].2004.1023-1028.

[12] KOO K, CHOI J, LEE J S. Parameter conditions for global stability of FAST TCP[J]. IEEE Communications Letters, 2008,12(2)∶155-157.

[13] CHOI Y J, KO J W, YUN S W, et al. Improved global stability conditions of the tuning parameter in FAST TCP[J]. IEEE Communications Letters, 2009, 13(3)∶ 202-204.

[14] JACOBSSON K, ANDREW L, TANG A, et al. An improved link model for window flow control and its application to FAST TCP[J].IEEE Transactions on Automatic Control, 2009, 54(3)∶ 551-564.

[15] WEI D. Microscopic Behavior of Internet Congestion Control[D]. Pasadena, California, USA∶ California Institute of Technology, 2007. 36-37.

[16] TANG A, ANDREW L L H, JACOBSSON K, et al. Window flow control∶ macroscopic properties from microscopic factors[A]. Proc IEEE INFOCOM[C].2008.91-95.

[17] TANG A, JACOBSSON K, ANDREW L L H, et al. An accurate link model and its application to stability analysis of FAST TCP[A]. Proc IEEE INFOCOM[C]. 2007. 161-169.

[18] CUI T, ANDREW L. FAST TCP simulator module for ns-2, version 1.1[EB/OL]. http∶//www.cubinlab.ee.mu.oz.au/ns2fasttcp, 2009.