基于信号子空间的ESPRIT-Like算法在相干DOA估计中的应用

张洪顺，许云林，湛江书

（1. 重庆通信学院 无线电管理教研室，重庆 400035；2. 重庆大学 资源与环境科学学院，重庆 400044）

1 引言

相干信号环境在现实中比较常见，如多径效应或是在军事通信中敌方有意实施干扰等情况，由于相干信号的影响，使阵列的空间协方差矩阵产生秩损失，从而使一些超分辨子空间类算法如多重信号分类[1](MUSIC, multiple signal classification)和利用旋转不变技术进行信号参数估计[2](ESPRIT, estimation of signal parameter via rotational inviance techniques)在相干环境中失去效用，相干信号的 DOA(direction of arrival)估计是空间谱估计亟需解决的一个实际问题。目前相干信号预处理方法包括：空间平滑类算法、矩阵重构算法和非降维处理算法[3]，但是这些算法都是以MUSIC作为DOA估计处理技术，由于MUSIC需要进行谱峰搜索，从而造成算法的运算量较大，且估计的稳健性不好。文献[4]提出了一种在相干环境下的ESPRIT-Like DOA估计算法，作者通过计算机仿真分析，验证了该算法的估计精度及解相关性能较空间平滑类算法及求根类算法都有明显改善，且算法运算量较低。

本文在相干环境中信号子空间维数讨论的基础上，提出了2种寻找包含所有信号信息数据矢量的方法，然后利用所得数据矢量重构得到一个Toeplitz矩阵，对其进行奇异值分解即可得到信号子空间与噪声子空间，最后利用ESPRIT方法进行DOA估计，即可得到所需结果。其中，本文第 2种数据矢量构造算法与文献[4]中的方法殊途同归。

2 窄带信道数学模型

假设空间存在P个远场窄带信号，包括M个信源经多径角度扩展得到的前L径相干信号（令各信源的最大径数分别为 l1,l2,…,lM）和后(P - L )个非相干信号，设信源统计独立；又设接收阵列为均匀线阵，包含N（ N ≥ P+1且N为奇数）个相同的全向阵元，阵元间距满足“半波长条件”即d≤λ2（λ为信号波长），如图1所示；信号DOA方向分别为θi( i = 1,… ,P ) ，假设空间噪声为理想的高斯白噪声，信号 si( t)(i = 1 , … ,P ) 与各阵元上的观测噪声统计独立。

图1 均匀线阵接收信号模型

以阵元1为参考阵元，则第k阵元上的观测数据可表示为

3 相干环境中信号子空间的维数

基于前面建立的理想高斯白噪声条件下的信道模型，计算阵列接收协方差矩阵：

(⋅)H为复值共轭转置，表示来波信号的协方差矩阵，σ2E表示噪声的协方差矩阵，σ2为噪声功率，E表示单位矩阵。由于假设阵列中理想阵元对信号来向是“敏感”的，即阵列对不同来向的信号具有不同的响应，由此可知，Vandermonde形式的阵列导向矩阵为列满秩的，即rank(A) = P。令信号协方差矩阵 RS的秩为对阵列接收矩阵进行特征分解，对其特征值进行非增调排序可得：

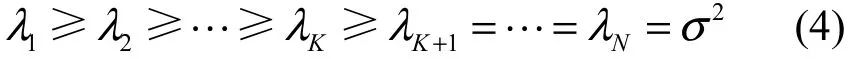
4 基于信号子空间的ESPRIT-Like算法

对相干信号的DOA估计包括解相干预处理与基于解相干基础上的DOA估计2个部分，目前关于解相干的预处理基本有两大类：一类是降维处理，可以分为基于空间平滑和基于矩阵重构2类算法；另一类是非降维处理，如频域平滑算法、Toeplitz方法、虚拟阵列变换法等。其中，基于降维处理的算法更为常用。本文在预处理中运用基于矢量奇异值的矩阵重构，首先设法寻找包含所有信号信息的数据矢量，经矩阵重构实现解相干的目的，而后利用ESPRIT方法进行DOA估计的处理。

4.1 构建包含所有信号信息的矢量

矩阵重构的目标是要使重构后的矩阵可以估计出相干信号源的信号或噪声子空间，因此，构建重构矩阵所需的数据矢量必须包含所有的信号信息。本文分析研究了2种构建包含所有信号信息数据矢量的方法，并在文章附录部分给出了相关定理的证明过程。

1) 方法1。

由特征分解的定义X=RV ΛV，其中，V为特征矢量矩阵，Λ表示对角形式的特征值矩阵，将式（3）代入式X=RV ΛV可得：

结合式（4）中的特征值分布情况可知，大特征值对应的信号特征矢量与矩阵 A RSAH的非零特征值对应的特征矢量是一致的。在此引出以下定理。

定理 1 假设 P （ P ≤ N-1）个窄带远场信号入射到N个阵元组成的阵列，则N×P阵列导向矩阵的秩为P，P×P信号协方差矩阵的秩为K（K≤P），又设噪声为理想高斯白噪声，N×N噪声协方差矩阵为满秩对角阵，则存在下列线形关系：

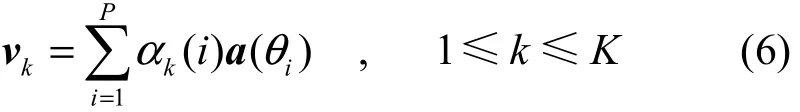
其中， vk(1 ≤ k ≤ K ) 表示信号特征矢量， αk( i ) 为线形组合因子，a ( θi)表示阵列接收第i个信号时的导向矢量（文献[5]中给出了该定理的频域表示形式，定理的详细证明过程见本文附录）。

定理1说明无论入射信号是否相干，对应大特征值的特征矢量是各信号导向矢量的一个线形组合，即包含了所有信号方向信息。为了提高后续DOA估计的精确性，本文在后续的仿真分析中对所有信号特征矢量进行求均，即有

2) 方法2。

在文献[6]中提出了一种直接针对数据处理，得到一组无噪声的快拍数据，同样可以获得一个包含所有信号信息的数据矢量：

其中，T为取样快拍数，xm表示1×T的任意一个参考阵元的接收数据矢量，X是N×T阵列接收数据矩阵，式中求数学期望也即对数据接收矩阵与参考阵元数据相乘后求时间平均。仔细分析可知，式（8）中的 em其实就是阵列接收数据协方差矩阵 RX的 第m(1 ≤ m ≤ N ) 行，在后续DOA估计的具体计算过程中可以对m进行求均，以提高DOA估计的精度[3]。

4.2 矩阵重构

为了利用上述2种数据矢量来实现解相干，本文利用获得的2个数据矢量v和 em重构得到如下2个Toeplitz矩阵，其中 Y1表示由方法1中的v重构所得，Y2为由方法2中的无噪声快拍数据矢量重构所得：

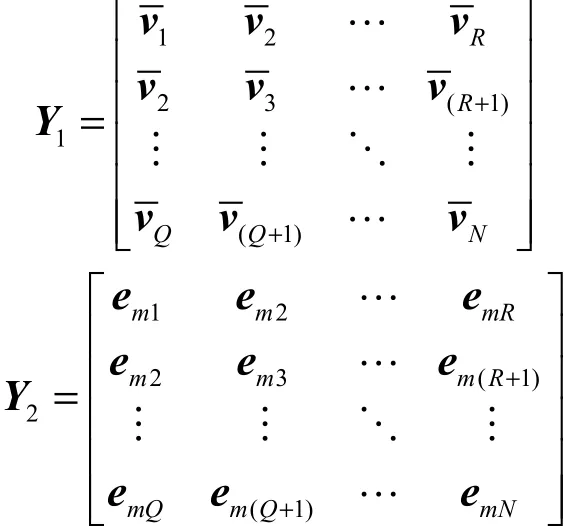
值得注意的是，式（9）中由无噪声快拍数据矢量经矩阵重构所得矩阵 Y2′ 与文献[4]中利用空间协方差矩阵直接重构得到的 Toeplitz矩阵 R ( m )在内容上是一致的，只是矩阵行的次序不同。分别对Y1′ 和 Y2′ 进 行奇异值分解有

其中，Λ1、Λ2为由奇异值构成的p×p对角阵，U1、U2为左奇异矩阵， V1、 V2为右奇异矩阵。由文献[6]中的证明过程可知， Y1′ 和 Y2′ 的大奇异值个数必为P，对应的左奇异矩阵 U1、 U2中的矢量组成的空间就是信号子空间，小奇异值对应的矢量组成的空间即噪声子空间。

4.3 DOA估计

为了利用信号子空间对所有来波信号的方向信息进行精确估计，本文注重利用方法 1构造的Toeplitz阵Y1′进行DOA估计（方法2中通过 Y2′实现DOA估计的具体过程可参考文献[4]）。为了进一步说明如何结合 E SPRIT方法对矩阵 Y1′进行DOA估计处理，将式（9）中的 Toeplitz阵 Y1′以信号协方差矩阵的形式表示为

由4.2节的讨论可知，对 Y1′进行奇异值分解可得P个大奇异值对应左奇异矩阵矢量组成的信号子空间和R-P个小奇异值对应矢量组成的噪声子空间

对 US进行同样分解，u 和 u 为 U 的第一行和最后一1RS行。由流型矩阵列向量张成信号子空间，即span{ ar( θ1) , … ,ar(θP)} = span{u1,u2, … ,uP}，从而必存在非奇异矩阵T满足进而可得

结合式（12）和式（13）有

其中， ( ⋅)-1表示逆矩阵，(⋅)+表示矩阵的 Moore-Penrose广义逆。令，对Ψ进行特征分解，其特征值即为进而估计出

5 数值仿真

在前面分析研究2种算法的基础上，本文利用MATLAB进行了大量Monte-Carlo实验。接收阵列为 11元等距均匀线阵，阵元间距为半波长，空间有3个完全相干信号，其载频为900MHz，设采样频率为采样点数为 N0=5 00个。

图 2 中各信号来波方向分别为5°、10°、30°，SNR= 3 0 dB 时进行20次独立试验所得结果，图中虚线为真实来波方向线，图2(a)为利用算法1所得数据矢量进行估计，图2(b)为采用算法2（即文献[4]中的方法）获取数据矢量进行的估计。从图2观察可知，2种算法均有较好的估计效果。

为了与空间平滑类算法进行比较，本文在SNR= 0 dB 条件下采用本文研究的2种算法和前向空间平滑算法[7,8]，分别对3个完全相干信号（来波方向分别为5°、10°、30°）进行20次仿真试验（见图3），由图3可以看出，在低信噪比情况下，前向空间平滑算法的谱峰分辨率明显降低，甚至不可分辨（见图3(c)），而本文2种算法的稳健性能较好，其中第1种算法有着更好的效果。

图3 本文算法与前向空间平滑算法DOA估计的比较

图 4为信号来波方向为 5-°、10°、5°时利用本文2种算法进行200次Monte-Carlo实验所得3个方向的平均估计偏差图，图5为相同条件下3个方向的平均估计均方误差（MSE）图。

表1 2种方法估计反应时间比较

6 结束语

本文在讨论相干信号环境特性的基础上，提出了一种基于信号子空间利用ESPRIT进行处理的相干DOA估计算法，理论分析及计算机仿真表明，利用本文算法对相干信号进行DOA估计有着较好的解相干性能，其中方法1的算法性能更优。该算法的最大优点在于运算量低，且在低信噪比条件下仍有较好的效果。但是根据理论分析可知，与空间平滑类等解相干算法相同，该算法是以牺牲有效阵元数为代价的。另外，该算法在其他特殊阵列中的应用方面还有待进一步研究。

附录 定理1的证明

为降低证明过程的复杂性，在此考虑最极端的情况，假设K=1（入射信号完全相干）， 接收信号完全由某个源信号与一组复值衰落因子相乘所得，S (t ) = Bs1(t)，其中，s1(t)表示唯一生成源信号， B = [ β1,β2,… ,βP]T为衰落系数向量，表示源信号 s1(t)第 i 径复值衰落系数。此时理想高斯白噪声条件下阵列接收信号的协方差矩阵为

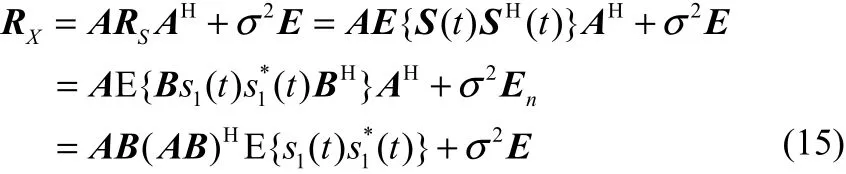
其中， ( ⋅)*表示复数共轭。对RX进行特征分解则有λ为唯一的大特征1值， v1表示该大特征值对应的 N × 1特征矢量，最后可以计算得到下式：

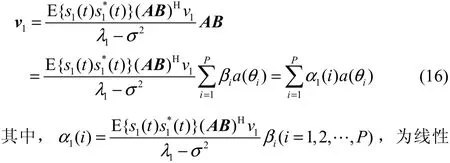
组合因子。在信号部分相干的情况下，可以同样利用该方法进行证明。

[1] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Trans on AP, 1986,34(3)∶276-280.

[2] ROY R, KAILATH T. ESPRIT—estimation of signal parameters via rotational invariance techniques[J]. IEEE Trans ASSP,1989,37(7)∶984-995.

[3] WANG Y L, CHEN H. Spatial Spectrum Estimation Theory and Method [M]. Beijing∶Tsinghua University Press, 2004.

[4] HAN F M, ZHANG X D. An ESPRIT-like algorithm for coherent DOA estimation[J]. IEEE Antennas and Wireless Propagation,2005,4∶443-446.

[5] CADZOW J A, KIM Y S, SHIUE D C. General direction-of arrival estimation∶ a signal subspace approach[J]. IEEE Trans on AES, 1989,2S∶ 31-47.

[6] GAO S W, BAO Z. Data matrix decomposition for super-resolution reconstruction of spatial coherences source[J]. Communication Journal,1988, 9(1)∶4-13.

[7] SHAN T J, WAX M, KAILATH T. On spatial smoothing for estimation of coherent signals[J]. IEEE Trans on ASSP,1985,33(8)∶806-811.

[8] LI H S, HOU T, ZHU Z D, et al. Performance of DOA estimation for correlated sources by forward-backward spatial smoothing [J]. Journal of Harbin Institute of Technology, 2007,3∶416-419.