CR-MIMO-OFDMA/TDM系统中基于效用的无线资源分配与调度

胡浩，宋俊德，慈松，唐晖

（1. 中国科学院 声学研究所，北京 100190；2. 北京邮电大学 计算机学院，北京 100876）

1 引言

多输入多输出正交频分复用(MIMO-OFDMA)是MIMO与OFDMA技术的联合，不仅具有MIMO技术高性能和容量的特点，还继承了正交频分复用(OFDM)技术抗符号间干扰和频率选择性衰落的优点。TDM 技术通过在相同的频率和空间上复用多个时间可分离的用户，可以获得更好的容量性能。因此，MIMO-OFDMA/TDM已成为3GPP (LTE, long term evolution)的核心技术之一，且广泛应用于无线城域网 (IEEE 802.16)和无线地域网 (IEEE 802.22)中[1～3]。由于目前绝大多数已存的无线网络仍使用固定频谱分配方式，无线频谱资源只能由本系统用户独享，因而频谱资源紧张的问题日趋严重。而认知无线电技术的出现[4,5]，实现了频谱的动态共享，为解决频谱资源不足、提高频谱利用率开创了崭新的局面。基于认知无线电的MIMO-OFDMA /TDM(CR-MIMO-OFDMA/TDM)系统可以实现主用户和认知用户的动态频谱共享，通过控制认知用户对主用户的干扰优先保证主用户通信，同时实现用户效用和最大化，保障用户的良好业务体验。

近年来，随着宽带无线网络的迅猛发展，越来越多的学者开始关注MIMO-OFDMA技术，而资源分配和调度问题是该研究领域的热点。Ying等人对MIMO-OFDMA系统中的动态子载波分配方案进行了研究[6]，将 SISO系统中的一种次优算法扩展到MIMO系统中，但没有考虑功率和速率分配；文献[7]研究了 MIMO-OFDMA系统中的公平性资源分配，但只考虑了总功率限制的情况；Mohammad等人提出一种基于自适应调制的多用户调度方案[8]，然而并未考虑其他限制条件。Ernest等人对于MIMO-OFDMA系统中的自适应资源分配问题进行了研究[9]，但并未考虑单个用户的速率限制，且无法实现用户调度。以上文献只研究了传统通信系统中的资源分配问题，而在认知无线电系统中，认知终端需要根据无线频谱的变化自适应改变传输参数，在不影响主用户业务的前提下实现动态频谱共享，因此需要建立新的模型来解决新问题。

针对上述问题，本文首先对多用户 MIMOOFDMA/TDM 认知无线电系统中的动态资源分配与调度问题进行了研究，针对不同业务设计合适的效用函数，并限制发射功率以控制认知用户对主用户的干扰，设置最小数据传输速率保证所有用户的满意度以最大化用户效用和；然后给出了一种动态资源分配与调度算法，松弛条件后进行拉格朗日对偶分解，并使用拉格朗日对偶法和次梯度迭代算法求解；最后给出仿真结果和分析。

2 CR-MIMO-OFDMA/TDM系统

2.1 系统描述

首先考虑单小区 CR-MIMO-OFDMA/TDM 系统，用户总数为K，基站端天线数目为M，用户移动台天线数目为N。基站与移动台之间为频率选择性衰落信道且信道被划分为 NT个子载波。为了提高系统频谱效率，本系统使用垂直分层空时码(V-BLAST)结构。基站端多用户数据流经过调度后分配到不同子带，各用户数据经过调制和VBLAST编码后映射到相应的子带上，通过 IFFT变换到时域加循环前缀后从M个发射天线进行发送。接收端N个接收支路去循环前缀后进行FFT变换将信号变换到频域，在各用户对应的子带上进行 VBLAST和多用户联合检测后，对不同子带上的用户信号输出进行合并，重判决后得到用户数据。认知用户终端能够通过频谱感知和信道估计获得无线环境状态信息并及时反馈给基站端，通过资源分配与调度模块实现基站端的用户调度以及各用户的功率与速率分配。系统下行链路功能模型如图1所示。

从频域角度看, 将系统总带宽分为Ns个相邻子带，每个子带由Ns个相邻子载波构成，子带宽度小于相干带宽，故可假设每个子带是平坦衰落的。 假设各子带的衰落是独立的，则各子带完全正交，不存在相邻信道干扰。从时域角度看，由于采用时分复用，可假设一个时隙内每个用户分配的子带数目不小于 1，而每个子带只可分给一个用户，定义用户调度因子 ρk,b= 1表示用户k占用子带b，则用户调度即在每个时隙中为所有子带选择最佳用户。

2.2 信道模型

单对天线之间的SISO信道在时隙n的复信道响应为 hk,l[n]，通过离散傅立叶变换得到在时隙 n上的用户k在子载波s上的信道功率增益为

图1 基于MIMO-OFDMA/TDM的认知无线电系统功能模型

其中，τl为信道多径时延，由于子带宽度小于信道相干带宽，可通过倒数平均法为每个子带计算等效信道增益。

其中，γk,b是第k个用户第b个子带的等效增益。不失一般性，假设用户k的子带b的MIMO信道矩阵为用户k的子带b中第k个子载波上的MIMO信道模型可表示为

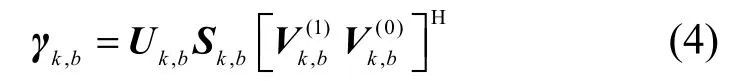
其中， [⋅ ]H表示矩阵的共轭转置，V(1)和V(0)分别为k,b k,b前个和后个右奇异向量组成的矩阵。 Vk(,0b)为γk,b零空间的一个标准正交基，可作为用户k在子带b上的发射预编码矩阵。为酉矩阵，表示接收解码矩阵。通过SVD分解可将用户k的子带b的MIMO信道矩阵分解为并行独立的多个SISO子信道，子信道个数P等于γk,b中非零特征值的个数且满足用户k在子带b的等效子信道p上的信道功率增益 γ(p)k,b即为中的第p个非零特征值，则占用子带b的用户k在子载波s上的接收信号向量可表示为

根据以上分析，用户k在子带b的第s个子载波上的接收信号向量可表示为

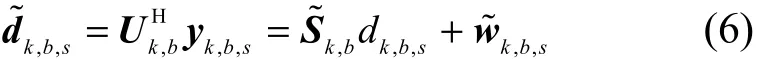
其中，,,kbsd 为用户k在子带b的第s个子载波上的经过调制后的数据符号，

3 动态资源分配与调度方案

3.1 方案描述

在认知无线电系统中，除了优先保证主用户业务质量，也要在不干扰主用户的前提下，为认知用户提供业务质量保障，因此本方案为所有用户设置最小数据速率限制保证业务 QoS(服务质量)需求，并使用微观经济学中的效用函数理论来评估用户对系统的满意程度。假设本系统中的业务为“弹性”业务，即用户对于网络提供的QoS的满意程度是通过数据速率来衡量的，则用户的效用函数 Uk(Rk)可代表用户k对系统的满意度， Rk为用户k的数据传输速率。由于用户满意度随着数据速率的增加而提升，因此该函数应该是递增的。而且，越靠近数据速率门限，用户的满意度上升越快，而远离该速率门限的地方，用户则不太在意速率的增长。所以，它的导数是递减的且为正值。因此，用户效用函数Uk(Rk)应该是一个非负且单调递增的凹函数。

本文主要考虑数据业务、语音业务和流媒体业务。对数据业务用户来说，对传输速率的要求不像语音和流媒体用户那么严格，但是数据速率下降造成的服务等待时间延长也会导致用户满意度下降，因此随着数据速率的下降，其效用函数值会逐渐下降；对于语音业务，当数据速率低于门限时，用户满意度非常低，而只要达到或超过门限后，用户满意度骤然提升；流媒体业务介于语音业务和数据业务之间，用户可以容忍一定的速率下降，然而在速率门限附近用户满意度变化幅度相比数据业务更大。

通过以上分析，本文选取Sigmoid函数设计不同业务的用户效用函数，其表达式如下：

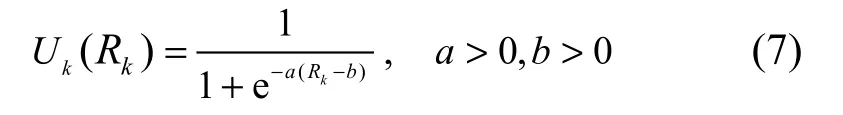
图2 数据、语音和流媒体业务的效用曲线

其中，参数a和b分别决定Sigmoid函数的斜率和坡度中点的位置。为3种业务分别选取不同的斜率a，并设置各用户的最小平均数据速率为坡度中点b，则数据业务、语音业务、流媒体业务的效用函数如图2所示。本系统中认知用户通过实时频谱感知探测主用户未使用的频谱并伺机共享，动态频谱共享中的核心问题就是如何控制认知用户对主用户的干扰。为了解决该问题，美国联邦通信委员会（FCC）提出干扰温度模型[12]，通过频谱感知获得主用户在特定位置和频段上可以忍受的干扰门限，并以此为依据对认知用户进行自适应功率控制以避免干扰。假设主用户集合与认知用户集合分别为MP和RC，则主用户ik处的干扰温度可由频谱感知获得[12]。

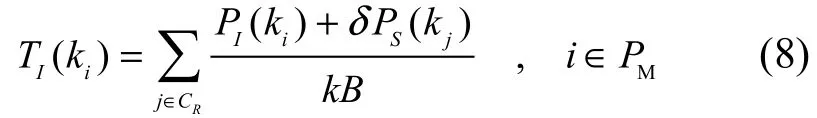
其中，B为带宽，PI( ki)和 PS(kj)分别为主用户 ki接收机处的干扰功率和认知用户 kj的发射功率；δ为路 径 损 耗 因 子 ，玻 尔 兹 曼 常 数为了控制认知用户对主用户的干扰，需使主用户在特定位置和频段上的干扰温度低于干扰温度限 T，即满足L

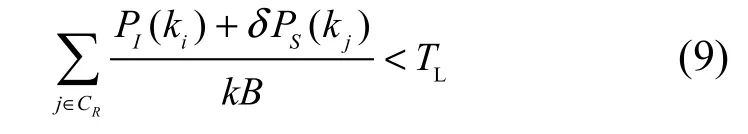
由式(9)可知，为了实现动态频谱共享并保证主用户通信，需要对认知用户的发射功率进行限制，本系统中由频谱感知模块获得各主用户干扰温度限，并计算满足式(9)的用户最小发射功率门限。

3.2 问题建模

通过以上分析，将 CR-MIMO-OFDMA /TDM系统中的动态频谱共享问题建模为最优化用户调度和动态资源分配问题，其目标是在一定的数据速率和发射功率限制下最大化用户效用和，即让用户满意度之和最大，则目标函数可表示为

其中， Rk(γ)为用户k的数据传输速率，数学期望通过信道衰落分布进行计算。若假设信道高斯白噪声方差为1，则由香农公式可得：

其中， P(p)(γ)为用户k在子带b的等效子信道p上k,b的发射功率，则本文的联合最优化问题可描述为

其中，kS和kP分别为用户k的最小数据速率限制和最大发射功率限制。

4 动态资源分配与调度算法

4.1 问题求解

由于实际系统中无法预知信道衰落分布和计算各用户数据速率的数学期望，本文首先采用Kushner等人文献中所使用的随机逼近法[10,15]对各用户数据速率的数学期望进行估计，则前n+1个时隙内用户k的速率期望值可用第n个时隙上的数据速率和前n个时隙内的速率期望进行近似。

联合最优化问题可转变为以下问题：

以上问题为一个非确定性多项式(NP-Hard)组合优化问题，传统解法复杂度高且难以实现，但是通过松弛约束条件，将用户调度因子松弛为时间复用因子ρk,b表示在一个时隙内子带b被用户k使用的比率，可将联合最优化问题转化为凸优化问题，若定义

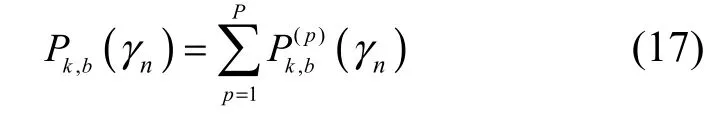
则目标函数可转化为

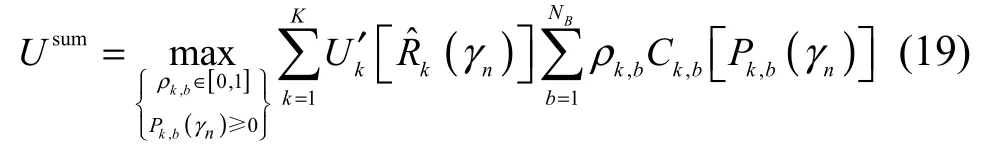
由于每个时隙上信道状态不变，因此可去掉数学期望Eγ[⋅]和γn。同时，由于上式中函数并不满足凹性，因此定义可行集，则以上问题可转化为如下问题：

给定凹函数 f (x)，则复合函数 g (x,t) = t f(x t)在t ＞ 0时也为凹函数，即在可行集上满足凹性。由于所有约束条件均为线性约束，因此上述问题为凸优化问题，可用拉格朗日对偶法[13]求解。若用ζk和ξk表示拉格朗日乘子，则该凸优化问题的拉格朗日函数为

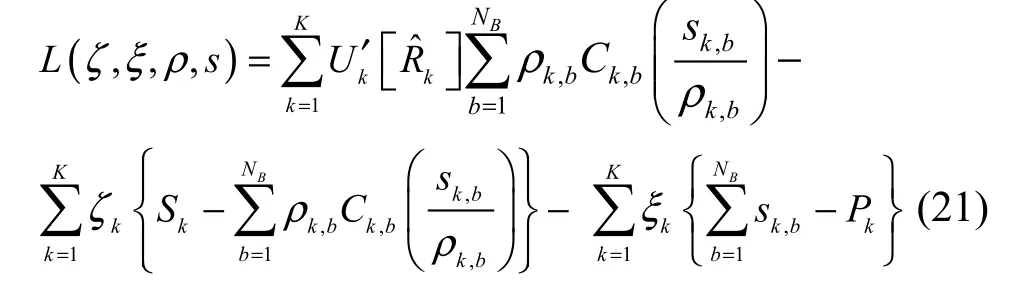
将式(18)和式(24)代入式(25)可得,kbφ∗：

将以上结果代入对偶问题，可将该问题转化为

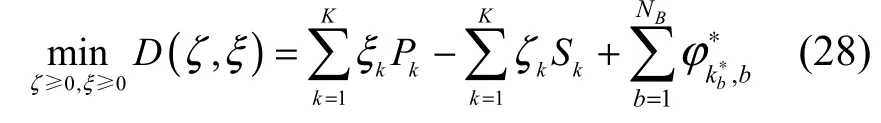
本文使用次梯度投影迭代算法[14]求解该问题，若定义对偶函数 D (ζ ,ξ)的次梯度Gζ和Gξ为

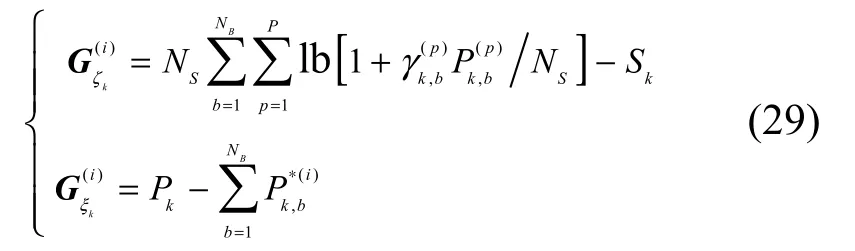
则次梯度投影算法迭代过程如下：

其中， ηi＞0为迭代步长。由于原始凸优化问题满足凸性且严格可行，因此对偶问题利用次梯度投影法可从任意非负初始值 ζk(0)和ξk(0)开始计算，最终可收敛至最优解[15]。

4.2 算法描述及复杂度分析

CR-MIMO-OFDMA系统中的动态资源分配与调度算法具体过程描述如下。

1) 在第n个时隙上，根据用户和业务类型获得该用户的最小速率门限，确定该用户业务对应的效用函数；通过信道估计和频谱感知获得主用户处的干扰温度限，确定各用户的最大发射功率限制。

① 计算子带b上各用户的发射功率 Pk∗,b；

② 将 Pk∗,b代入φ˜k∗,b，由于可计算使φ˜k∗,c最大的用户该用户独占子带b。

4) 重复第 2)步和第 3)步，直至满足收敛终止条件，如：为预先指定的任意小数。通过式(13)计算，下一个时隙重新回到第1) 步。

以上算法需要根据式(26)为每个用户在所有子带上计算φk∗,b，因此该算法复杂度与用户数目和子带数目成线性关系，每次迭代过程中的计算复杂度为 O (K NB)，远低于组合最优化问题的计算复杂度O(NKB)。相比传统方法[16]，本文算法复杂度更低。

5 仿真结果及分析

本节设计了3个计算机仿真实验对动态资源分配与调度算法进行验证。假设系统带宽10MHz，子载波总数NT=256，子带总数NB=16，则子带内包含16个子载波，信道模型为频率选择性块衰落模型。OFDM帧长2ms，每帧的时隙数为5。

实验1最优化资源分配与用户调度

实验1考察算法收敛时系统的用户调度和最优化资源分配结果。仿真过程中信道估计与频谱感知均为理想信息。假设基站与移动台天线数目均为2，用户总数K = 4，其中用户1为主用户，其他用户为认知用户，假设各用户的最小平均速率限制为4，2，1, 0.5(单位bit/s/Hz)；最大平均发射功率限制为100, 60, 30, 20(单位mW)。其中主用户与认知用户1都使用流媒体业务，认知用户2和认知用户3分别使用语音和数据业务，则用户效用函数可定义为

图3为各用户的效用函数曲线，均满足用户所使用业务对效用函数的需求且坡度中点为各用户的数据速率门限。

图3 使用不同业务的用户效用函数曲线

如图4所示为算法收敛时的最优化用户调度结果，其中主用户占用6个子带，3个认知用户分别占用5、2、3个子带。为了最大程度地满足主用户业务需求，主用户的最小速率门限高于所有认知用户最小速率门限，结果显示，主用户分配的系统资源大于所有认知用户，从而保证了主用户效用。

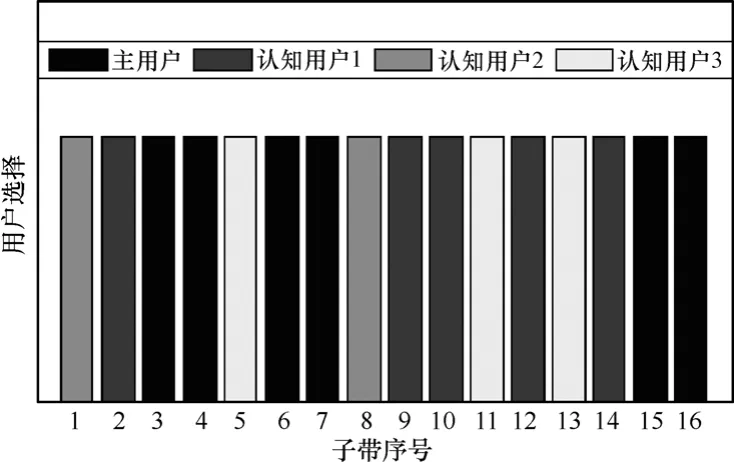
图4 用户最优化调度

图 5为算法收敛时用户最优化速率和功率分配。仿真结果显示，该算法收敛时各用户发射功率满足动态频谱共享的最大发射功率限制，而传输速率也满足保证业务QoS需求的最小平均速率限制。

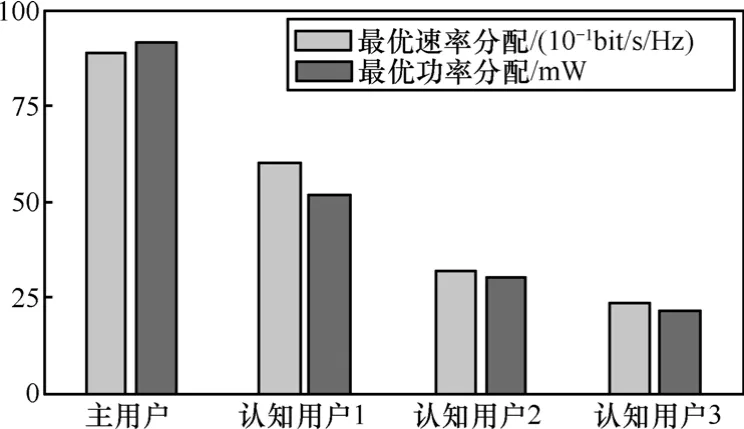
图5 用户最优化速率与功率分配

图6 为各用户的效用曲线，由于主用户和认知用户1设置了较高的数据速率门限，所分配的系统资源较多，算法收敛时效用趋近于 1；而其他认知用户需要降低自身效用来保证主用户和认知用户 1的效用，因而效用曲线呈下降趋势。认知用户2使用语音业务，其效用受传输速率影响大于数据业务，所以相比认知用户3其效用曲线下降速度更快。

图6 用户效用曲线

实验2算法性能比较

实验2旨在考察不同用户数目下使用本文算法与平均分配算法以及主用户占优算法的性能。其中，平均分配算法为所有用户平均分配子带，即无用户调度；主用户优先算法优先保证主用户数据传输，只为各认知用户分配一个子带，剩余子带全部分配给主用户。在实验中选择用户总数分别为2、4、8、16、32，其中主用户数目为 1、1、2、2、4。VBLAST多天线系统选择为M = N = 2。对每种算法分别进行5 000次Monte Carlo仿真实验后比较3种算法的归一化用户效用和。

如图7所示为3种算法的归一化效用和，容易看出本文算法性能优于另外2种算法。当用户数目较少时，主用户效用为系统效用贡献最大，因此主用户优先算法性能优于平均分配算法，随着认知用户继续增加，主用户效用对系统效用所做贡献逐渐下降，主用户优先算法性能下降。随着用户数目增加，主用户优先算法为某些认知用户分配的系统资源不足以提供高于门限值的数据传输速率，因此用户效用和急剧下降，性能远低于本文算法。

实验3算法收敛性

实验3考察本文算法的收敛性。图8为各用户平均速率与功率分配过程，图中的虚线表示各用户的速率和功率门限。仿真表明，通过该算法所有用户可快速收敛至满足速率和功率限制条件的最优速率和功率。如图9所示为算法中的拉格朗日乘子ζ和ξ 的 收 敛 过 程 。 本 实 验迭 代 步 长容易看出，本文算法能以较快速度收敛至最优解，适合在实际系统中使用。

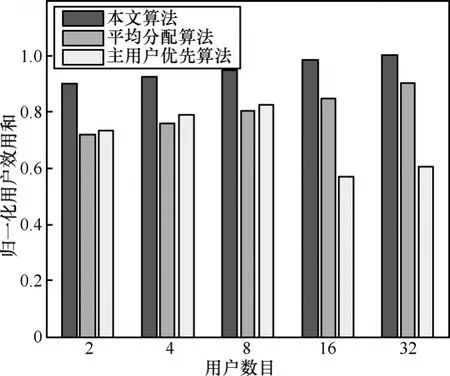
图7 3种算法的归一化用户效用和比较

图8 系统最优化速率与功率分配过程

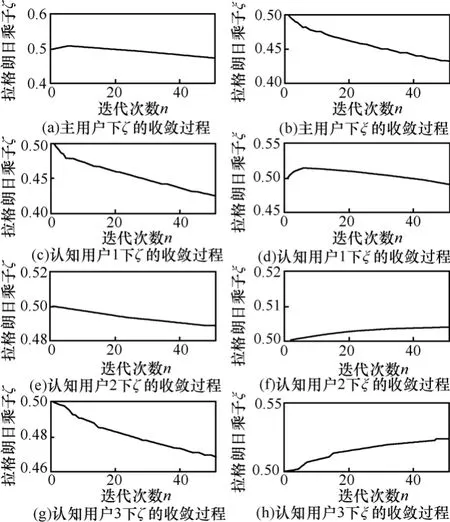
图9 拉格朗日乘子ζ和ξ的收敛过程

6 结束语

多用户MIMO-OFDMA/TDM认知无线电系统中的动态资源分配与调度问题需要在用户功率和速率限制下最大化用户效用和，是一个NP-hard组合最优化问题，本文通过松弛约束条件将其转化为凸优化问题，使用拉格朗日对偶法将原始问题转化为新的对偶问题，通过使用拉格朗日求导法与次梯度迭代算法求解对偶问题可获得原始问题的最优解。仿真表明该方案可以最大化用户效用和，获得主用户与认知用户的最优功率/速率分配同时实现用户调度，且算法复杂度较低收敛较快适用于实际通信系统。需要指出的是，本文所提出的方案是建立在信息完全的频谱感知和信道估计基础之上的，虽然通过划分子带减少了部分信令，但在实际应用中仍需要较大的反馈量。因而，如何在基站端已知部分信道信息的情况下设计出更具顽健性的资源分配和调度方案便成为亟待解决的关键问题，在以后的工作中将继续对此进行深入研究。

[1] WUNDER G, CHAN Z. Queueing analysis for the OFDMA downlink∶Throughput regions, delay and exponential backlog bounds[J]. IEEE Trans on Communications, 2009, 8(2)∶871-881.

[2] ETEMAD K. Overview of mobile WiMAX technology and evolution[J]. IEEE Communication Magazine, 2008, 46(10)∶31-40.

[3] STEVENSON C, CHOUINARD G, et al. IEEE 802.22∶ The first cognitive radio wireless regional area network standard[J]. IEEE Communication Magazine, 2009, 47(1)∶ 130-138.

[4] MITOLA J, MAGUIRE G Q. Cognitive radio∶ making software radios more personal[J]. IEEE Personal Communications, 1999, 6(4)∶ 13-18.

[5] HAYKIN S. Cognitive radio∶ Brain-empowered wireless communications[J]. IEEE Journal on Selected Area in Communications, 2005,23(2)∶ 201-220.

[6] YING P, ARMOUR S M D, et al. An investigation of dynamic subcarrier allocation in MIMO-OFDMA systems[J]. IEEE Trans on Vehicular Technology, 2007, 56(5)∶ 2990-3005.

[7] JIAN X, JONGKYUNG K, et al. Adaptive resource allocation algorithm with fairness for MIMO-OFDMA system[A]. Proc of VTC[C].2006.1585-1589.

[8] MOHAMMAD T, WESSAM A, et al. Multiuser scheduling for MIMO-OFDM systems with continuous-rate adaptive modulation[A].Proc of IEEE WCNC[C]. 2008.946-951.

[9] ERNEST S L, CHAN PETER W C, et al. Adaptive resource allocation and capacity comparison of downlink multiuser MIMO-MC-CDMA and MIMO-OFDMA[J]. IEEE Trans on Wireless Communications,2007, 6(3)∶1083-1093.

[10] KUSHNER H, YIN G. Stochastic Approximation Algorithms and Applications[M]. Berlin, Germany∶ Springer-Verlag, 2003.

[11] GAO J, FAULKNER M. On implementation of bit-loading algorithms for OFDM systems with multiple-input multiple- output[A]. Proc of IEEE Vehicle Technol Conf (VTC) ’02-Fall[C]. 2002.199-203.

[12] FCC. Establishment of Interference Temperature Metric to Quantify and Manage Interference and to Expand Available Unlicensed Operation in Certain Fixed Mobile and Satellite Frequency Bands[Z]. ET Docket 03-289, Notice of Inquiry and Proposed Rulemaking, 2003.

[13] BOYD S, VANDENBERGHE L. Convex Optimization[M]. Cambridge University Press, 2004.

[14] BERTSEKAS D, Nonlinear Programming[M]. 2nd Ed, Athena Scientific, 1999.

[15] XING W, GIANNAKIS G B, MARQUES A G. A unified approach to QoS-guaranteed scheduling for channel-adaptive wireless networks[J].Proceeding of the IEEE, 2007, 95(12)∶ 2410-2431.

[16] GUOCONG S, YE L. Cross-layer optimization for OFDM wireless networks-Part II∶ algorithm development[J]. IEEE Transactions on Wireless Communications, 2005, 4(2)∶ 625-634.