基于SMP的无线传感器网络拓扑容侵定量评估

熊书明，王良民，詹永照

(江苏大学 计算机科学与通信工程学院，江苏 镇江 212013)

1 引言

布置在恶劣甚至恶意环境下的无线传感器网络(WSN, wireless sensor networks)，常会因为随机故障或者入侵威胁等形成节点失败，需要发起新的拓扑生成操作。目前，针对拓扑控制的研究主要集中在容错[1～4]和容侵[3～5]的拓扑生成和更新方面，容忍入侵机制在WSN的安全保障方面受到越来越多的关注。然而，容侵拓扑更新和自再生操作会影响到作为支持上层路由操作的拓扑连通服务，可能导致拓扑割裂；同时，频繁的拓扑安全更新操作必然增加网络不必要的资源开销，缩短了恶意环境下传感器网络的生命期。因此，需要研究安全拓扑构建模块的容侵性能定量评估，为发起新一轮拓扑自再生操作提供决策依据。

Albert[6]最早针对有线复杂网络结构，利用统计分析的方法探讨影响拓扑容侵能力的因素。在无线传感器网络容忍入侵能力评估的研究中，Wang[3]较早从拓扑容错和容侵角度研究WSN拓扑对节点失败的容忍能力，对分层拓扑容侵能力给出了定性评估。Ma[4]主要考虑在传感器网络路由层次上，以多版本多路径思想来确保数据传输的容忍能力，提出了一个容侵/容错的3层通用模型MVMP框架进行容忍能力的评估。Wang[5]在面对入侵的环境下，基于三色思想提出了具有较强容侵能力的传感器网络拓扑生成算法，从理论上对拓扑容侵能力进行了分析推导，并依据容忍能力适时启动拓扑自再生。然而，这些工作并没有给出评估拓扑容侵能力的衡量指标；而且，针对传感器网络的拓扑容侵，现有工作多数仅仅强调拓扑对失败容忍能力的保证，一般仅从定性分析的角度来评估拓扑的容忍能力，由此影响到容侵拓扑更新的合理决策。本文提出了基于半马尔可夫过程(SMP)的无线传感器网络拓扑容侵定量评估模型，结合Bayes推理网络对拓扑可用性、稳定性和服务率指标进行了定量分析，能够准确评估拓扑容侵能力，便于传感器网络拓扑结构的重新配置。

2 拓扑容侵能力评估的状态变迁模型

2.1 基于SMP的拓扑容侵状态转移模型

传感器网络会受到诸如 DoS、Hello洪泛、污水池和 Sybil等攻击[7]，导致拓扑构建出现安全失败。本节提出了基于 SMP的拓扑容侵状态转移模型，描述攻击导致的拓扑容侵状态变化和容侵模块应对攻击所处的各种状态。

定义 1 拓扑容侵状态转移模型是一个有序四元组，如式(1)所示:

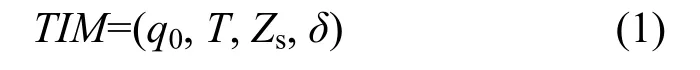
其中，q0∈Zs是容侵拓扑构建模块的初始状态N，T是离散时间集，描述了各状态的一个离散时间序列，Zs={N、S、I、F、GD、UD}是容侵模块的状态集，而δ是控制状态转移规律的T×Zs到T×Zs映射。

根据定义1，容侵拓扑构建过程从初始态q0开始，在离散时间序列上，由δ控制拓扑容侵状态的转移，图1给出基于半马尔可夫过程的容侵拓扑状态转移过程。通常情况下，入侵者对拓扑构建过程的攻击影响和拓扑容侵模块对恶意攻击的类型、强度、持续时间及攻击频率等的认识都存在一定的不确定性。模型TIM以一定的概率来描述状态间的变迁，从而可以分析系统处于各状态的概率。

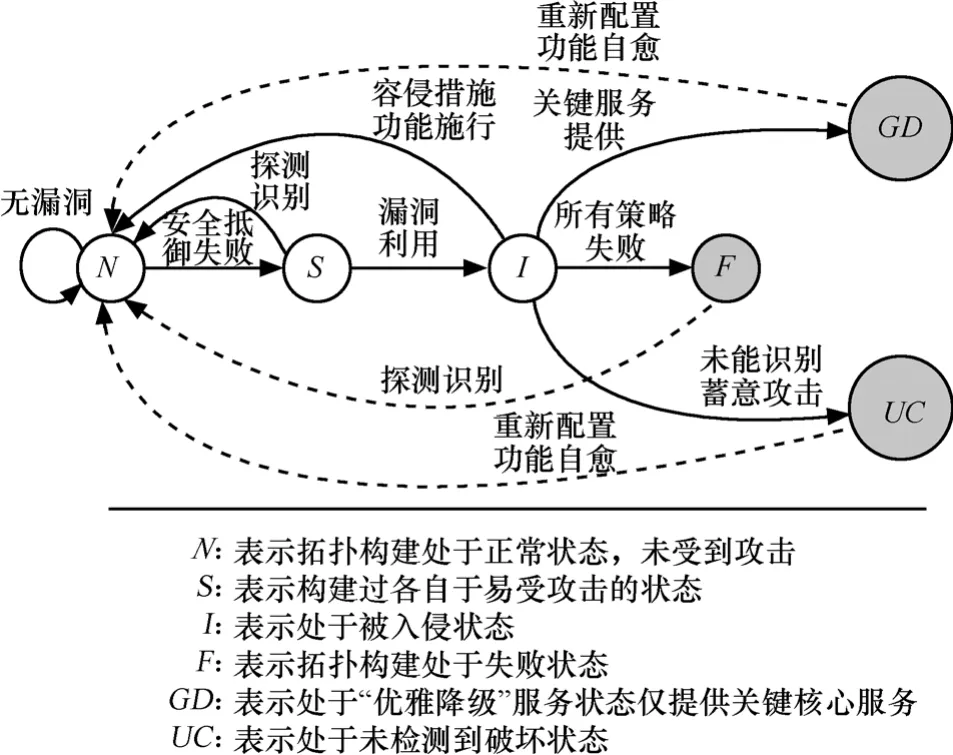
图1 容侵拓扑构建的状态迁移

图1中，拓扑构建初始时处于正常状态N，各种典型的安全机制正常工作。安全机制不能抵御入侵时，系统进入敏感状态S，入侵者通过多种探测技术已发现拓扑构建模块的脆弱性，发起了针对拓扑生成的攻击。如果攻击者成功利用系统漏洞，则进入状态I，系统被入侵，此阶段容侵机制可以利用资源冗余、大数表决等来减少入侵带来的危害。由于容侵机制的安全强度不同，攻击行为可能造成的危害也不一样，如果容侵机制未能检测出针对拓扑的攻击，则进入 UC状态，拓扑控制模块不能采取任何抵御措施，最终出现拓扑割裂。如果检测到攻击行为，则容侵模块以一种“优雅降级”的服务方式，保证关键服务的持续性，进入 GD状态，但需人工干预恢复到正常状态；否则，完全失控进入状态F。

分析该状态迁移过程需要2个参数，包括状态的逗留时间和状态间的转移概率。

定义2 hi是拓扑模块在状态i的平均逗留时间，i∈Zs；pij是状态 i、j间的转移概率，i、j ∈Zs。

2.2 容侵能力评价指标

针对无线传感器网络拓扑容侵能力的分析，考虑拓扑可用性(TA)、拓扑稳定性(TS)和拓扑服务率(TRoS) 3个指标。主要从评价拓扑容侵能力的角度直接分析拓扑构建过程中各状态的变迁，忽略一些入侵者具体的攻击手段和拓扑容侵机制的响应细节。3个评估指标的定义如下。

定义3 拓扑可用性TA。它是指在概率意义下容侵拓扑构建到达稳定状态时，拓扑模块提供连通服务的概率PTA。

可用性分为瞬时可用性和稳态可用性[8]，定义3指的是拓扑稳定状态下的可用性，着重描述容侵拓扑在攻击影响下的服务能力。在图1中，设拓扑不能提供服务的状态集合为STA#，πi(i∈Zs)是在稳态意义下状态i所处的概率，可以给出拓扑可用性如下数学描述:

定义4 拓扑稳定性TS。在容侵拓扑构建到达任一吸收态SA之前，拓扑构建处于未受攻击状态N的时间与处于临时态SA#总时间的比值PTS。

吸收态反映了系统最终会陷入一种自动不可恢复状态，只有等待人工干预。临时态反映了状态迁移过程中，系统所处的多个中间状态。

TS描述了容侵拓扑构建模块的安全入侵容忍能力，可为拓扑容侵能力的重新配置提供参考依据,形式化描述如下:

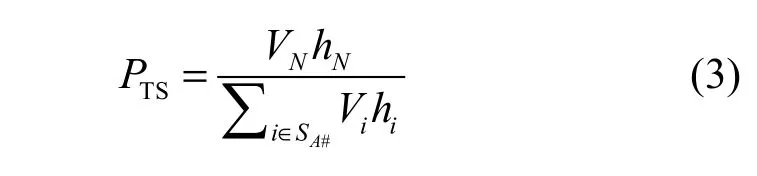
其中，Vi和hi分别表示在到达任一吸收态之前处于状态i的次数和平均逗留时间。

定义5 拓扑服务率TRoS。它是指平均安全故障时间(MTTSF)在一个拓扑服务周期内所占的比例PTRoS。

MTTSF给出了拓扑构建过程在进入某一吸收态之前所持续的时间，但是在面对安全入侵时，拓扑构建最终会以某种概率进入相应的吸收态，拓扑服务率TRoS反映了容侵模块在整个工作期间有效工作时间占的份额，设在概率意义下，一个拓扑服务周期是T，拓扑服务率数学定义如下所示:

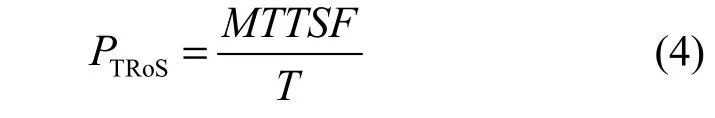
综合上述指标，利用函数 f 描述拓扑容侵能力值PCoIT随评估指标变化的关系，如式(5)所示:

3 DTMC的容侵指标求解及能力评估

3.1 DTMC的形式化描述

从基于 SMP的状态迁移模型可知，容侵拓扑构建模块在各状态之间的迁移满足马尔可夫性，即将来的状态仅取决于当前的状态，且在离散时间序列上进行状态间转变。因此，采用离散时间马尔可夫链(DTMC)对整个的状态迁移进程进行分析，图2描述了 SMP的嵌入马尔可夫链，其形式化描述由定义6给出。

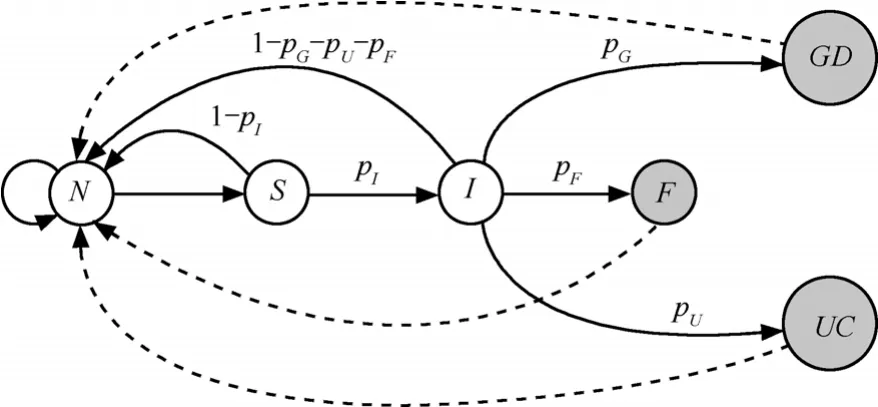
图2 拓扑容侵评估的DTMC模型

定义 6 离散时间马尔可夫链(DTMC)是一个有序六元组，如式(6)所示:

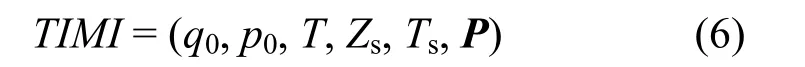
其中，q0、T和Zs的含义同SMP模型，Ts={hN, hS,hI, hF, hG, hU}是拓扑构建模块处于各状态的平均逗留时间，P是各状态间的迁移概率矩阵，由图 2可知，矩阵P可表示为

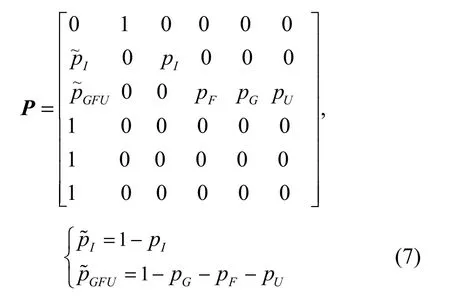
矩阵 P的行列都以N，S，I，F，GD，UC顺序排列。有关状态转移概率和平均逗留时间使用的符号及含义如下所示。

pI:脆弱状态下，进入入侵状态的概率。

pF:所有容侵策略均失败的概率。

pU:未检测到成功入侵的概率。

pG:拓扑服务优雅降级的概率。

hN:容侵拓扑构建处于正常状态的平均时间。

hS:脆弱状态下，构建模块遭受入侵的平均时间。

hI:在入侵状态，拓扑容侵模块决策的平均时间。

hF:容侵策略失败时，恢复到正常态的平均时间。

hG:拓扑在降级状态下的平均持续时间。

hU:攻击成功时，未能检测到入侵的平均时间。

3.2 指标求解

3.2.1 拓扑可用性

为计算拓扑可用性，需要得到 SMP模型中各状态的稳态概率，首先求出DTMC模型中各状态的稳态概率。

在图2的DTMC模型中，根据文献[9]可得:

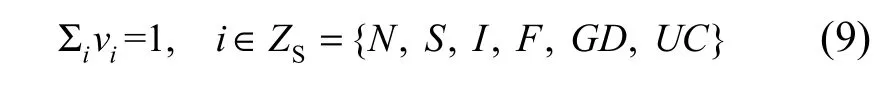
联立式(8)和式(9)求解，得 DTMC模型中稳态意义下状态的概率向量v:

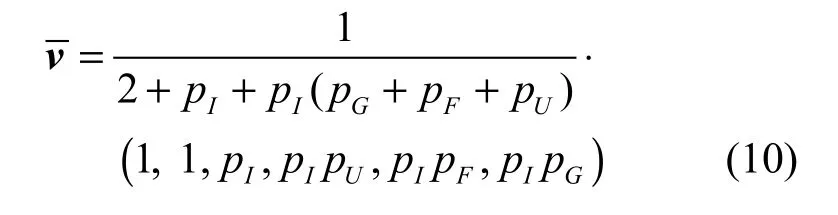
采用文献[9]提出的方法，得到SMP各状态稳态概率的计算公式如下:

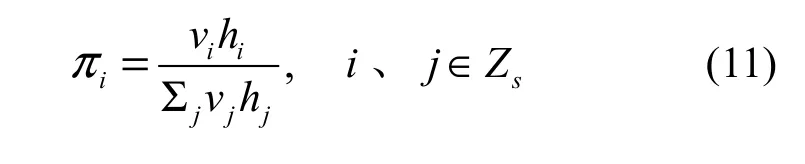
其中，vi是DTMC中各状态的稳态概率，hi是状态i的平均逗留时间，因此，需要确定每个状态的平均逗留时间。hi往往取决于入侵者的攻击能力、安全模块的防护强度和容侵拓扑构建模块的容忍能力等诸多因素，具有不确定性和随机性，故在各状态逗留时间的概率分布往往呈现多样性。本文从渐进意义上考虑容侵状态的平均逗留时间，所以，根据文献[8]可以假设在状态N、S、I实际服从Weibull(λ, k)分布，而在状态F、GD、UC服从gamma(k, θ)分布。在状态N和F的期望逗留时间可表示为

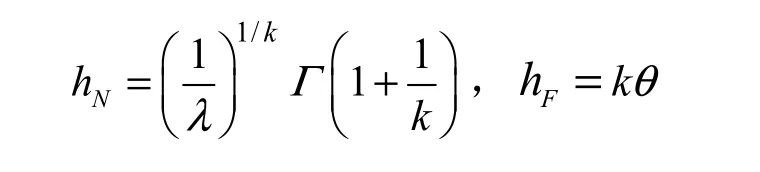
联立式(10)和式(11)求解，得SMP模型中各状态的稳定概率向量Π:

如图1所示的SMP模型中，拓扑构建模块处于 F、UC状态时，容侵模块没有检测出对系统的攻击和虽然已检测出但不能采取有效容忍措施，不能提供拓扑连通服务，即在这2个状态下拓扑不具可用性，所以集合STA#={F, UC}，由式(2)和式(12)得计算拓扑可用性TA的公式如下:

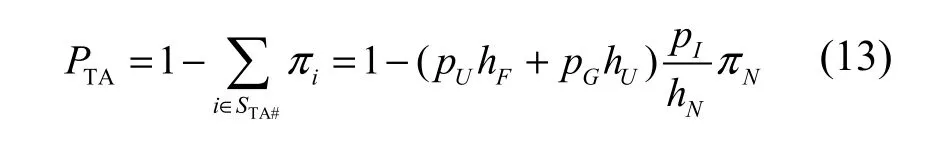
3.2.2 拓扑稳定性

定义4指出，可将DTMC的状态分为临时态Zt和吸收态Za。图2中，拓扑构建过程一般在N、S、I 3个状态之间来回振荡，只有在容侵机制不能正常发挥效用时才进入F、GD、UC中的任一状态，等待人工干预。因此，Zt={N、S、I}，Za={F、GD、UC}，对应临时态Zt和吸收态Za的状态迁移概率矩阵P'如下:

按照临时态和吸收态两两组合的4种情况划分为4个区域，右上角子矩阵设为C。

设Vi是到达任一吸收状态前，在临时态i的平均次数，计算Vi的公式如下:

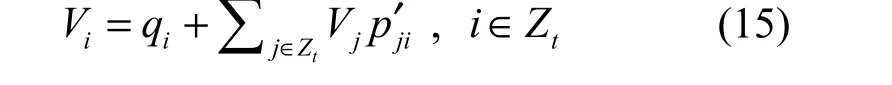
其中，qi是初始状态为i的概率，本文假设状态N是初始状态，有[qi]=[1, 0, 0]。

解式(15)得到处于各临时态的平均次数向量V:

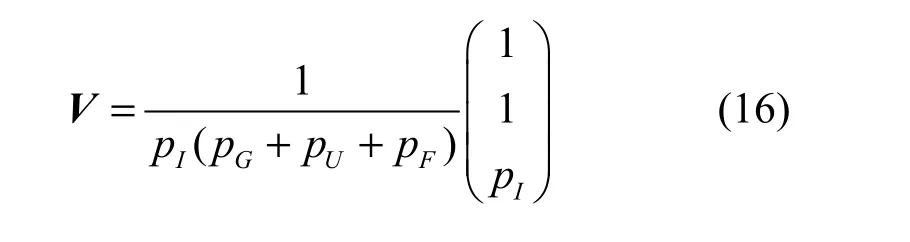
联合式(3)和式(16)，结合各临时态的平均逗留时间hi，可得拓扑稳定性TS的值。

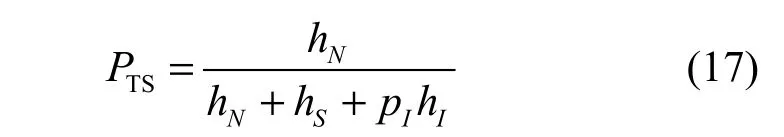
3.2.3 拓扑服务率

拓扑服务率TRoS可以很好地刻画整个拓扑服务周期内的有效工作时间份额，反映了容侵拓扑模块在一定攻击下的整体服务能力，针对拓扑构建的不同攻击威胁将导致进入不同的吸收状态，相应地，其危害也不一样。利用文献[8]提出的方法，计算平均安全故障时间MTTSF和由初始状态N进入各吸收态的概率b1j公式如下:

联立式(16)和式(18)求解得:

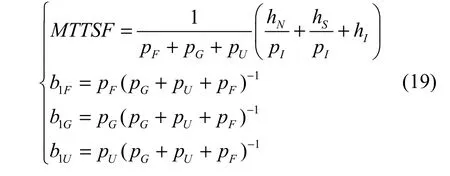
由式(4)和式(19)求解拓扑服务率TRoS得:

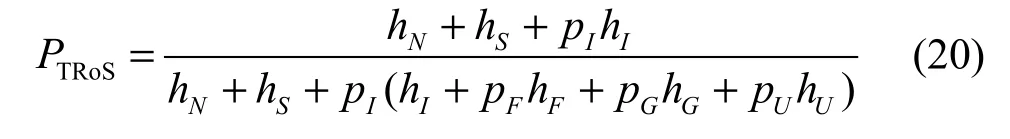
3.3 基于贝叶斯网络的综合指标分析

文献[10]指出，近年来贝叶斯网络(BN, Bayes network)模型在可靠性分析领域中的应用逐渐得到关注，本文提出一个BN模型来预测、评估无线传感器网络拓扑容侵能力和各项评价指标对容侵能力的影响度。

图1所示的状态迁移模型从概率的角度分析、计算拓扑可用性、稳定性和服务率，这其中蕴含着一定的统计特性和内在联系。为对拓扑容侵能力和其与各属性的相互关系进行预测及统计推断，设计的贝叶斯网络模型如图3所示，形式化描述为G=(N, R)，N代表图G中4个节点的集合，R代表推理图中相邻2个节点间依赖关系的集合。

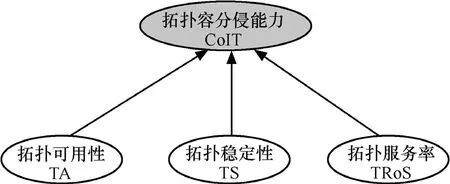
图3 拓扑容侵能力评估的贝叶斯网络模型

拓扑容侵能力CoIT可通过拓扑可用性TA、稳定性TS和服务率TRoS及它们与拓扑容侵能力的关系来深入度量。根据先验知识，假设TA、TS和TRoS在描述拓扑容侵能力CoIT时可信的概率分别为 P(θTA)、P(θTS)和 P(θTRoS)，这 3 个值可通过评估过程中获得的信息进行后验分析加以不断改进，使它们逼近真实值。根据定义3、定义4和定义5，这3个指标分别从不同角度刻画拓扑容侵能力，它们在描述容侵能力这一事件的样本空间上互不相容，构成一个划分；同时，以概率P(CoIT)来描述拓扑容侵能力的强弱(1最强，0最弱)。基于贝叶斯网络推理规则，CoIT与TA、TS和TRoS 3个指标的关系可通过图3节点之间的连接关系来形式化描述。在拓扑可用性以先验概率 P(θTA)可信的前提下，它导致拓扑容侵能力以条件概率P(CoIT|θTA)发生(该值反映了从拓扑可用的角度表示容侵能力的强弱，可由前述的DTMC计算得到，即PTA)。由全概率公式得:

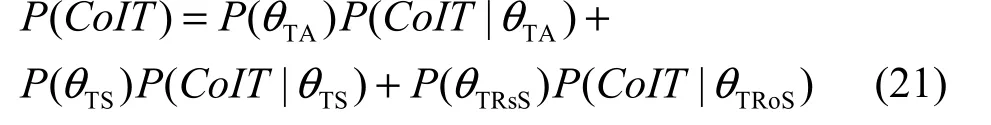
式(21)表示在已知 3个拓扑容侵能力衡量指标的可信概率下，利用3个指标所反映容侵能力的当前值，综合评判得出拓扑容侵能力的强弱，刻画了3个指标与综合值之间的关系。

此时，对TA有以下条件概率公式成立:

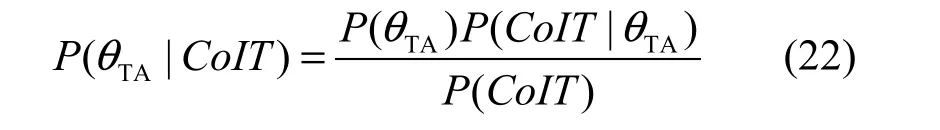
同理，对稳定性和服务率有类似的分析。

4 拓扑容侵能力分析与评价

4.1 模型工作参数

不失一般性，选取 pI和 hN参数分析其对不同指标和拓扑容侵能力的影响。

1) 状态迁移概率

在图2描述的DTMC模型中，PG是拓扑构建模块从状态I进入优雅降级状态GD的概率，以实现拓扑功能的核心服务，不妨设PG=0.2。在I状态下，未能检测到恶意节点的入侵概率是PU，其值设为 0.2，该状态下容侵模块完全不可操控而进入失败状态F的概率较小，设PF=0.1。

2) 状态平均逗留时间

设时间单位是 1，在脆弱状态下，入侵者发现漏洞、拓扑构建模块遭受入侵的平均时间hS=0.2，容侵模块在入侵状态下进行多种控制决策的平均时间hI=0.4。在容侵策略失败时，系统恢复到正常状态所需的平均时间hF=0.7，同理，设在降级状态下的平均持续时间hG=2，入侵成功时，未能检测到入侵的平均时间hU=3。

4.2 拓扑容侵能力的参数敏感性

如图4(a)所示，平均安全故障时间MTTSF随参数pI变化明显，当pI超过一定阈值时，MTTSF表示的拓扑安全绝对时间显著减少，在较低的pI取值时，MTTSF随hN线性增长。因此，为提高容侵拓扑模块一次工作的有效时间，应确保较低的pI取值，即需要增强拓扑容侵模块的防护强度。图4(b)描述了拓扑服务率随hN递增和随pI递减的趋势。当 pI和hN取值都较大时，尽管有较高的拓扑服务率，但是绝对服务时间非常短，所以，在较高的拓扑服务率下，拓扑构建模块的容侵能力可能呈现出某种振荡特性，此时需要较多的外部干预。

图4 平均安全故障时间和拓扑服务率随hN和pI的变化趋势

图5(a)给出了拓扑容侵能力PCoIT随hN递增，而随pI递减的函数变化趋势。由图5(a)可知，为了提高容侵拓扑模块的容侵能力，在给定工作参数下，必须增加在状态N的hN和减少进入入侵状态I的概率pI来保证。图5(b)给出了拓扑可用性的后验概率可信度 P(θTA|CoIT)随 pI递增和随 hN递减的趋势，说明如果希望增加可用性在衡量拓扑容侵能力中的权重，可通过提高进入入侵状态I的概率pI的值或减少处于正常状态N的平均逗留时间hN实现。

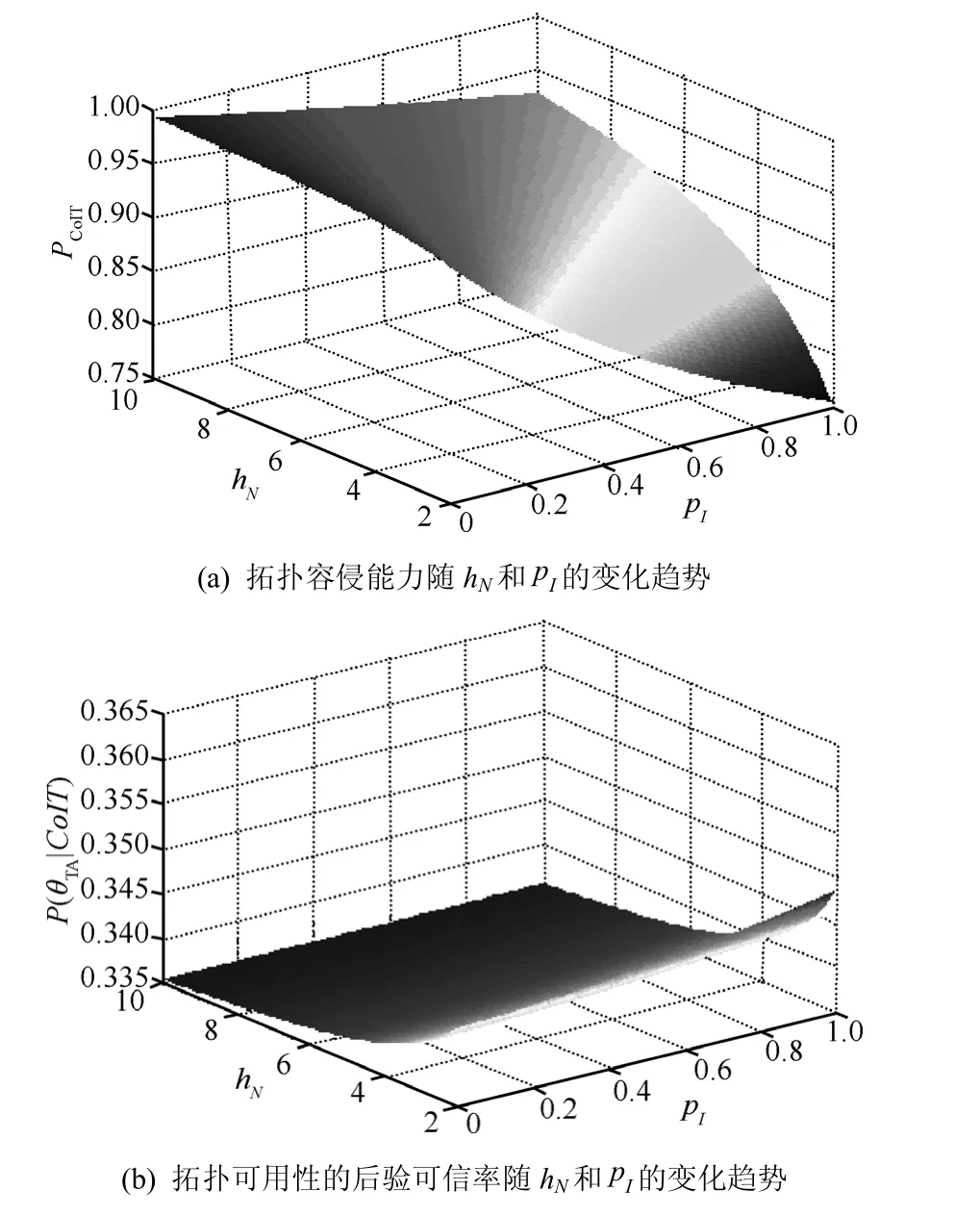
图5 拓扑容侵能力和拓扑可用性的后验概率随hN和pI的变化趋势

4.3 拓扑容侵实例剖析及模型验证

本节对LEACH[11]和ASCENT[12]2个实际的拓扑构建机制进行容侵能力分析，以评估模型的有效性。

4.3.1 Sybil攻击的模型评估能力分析

Sybil攻击时，恶意节点会伪造多个节点身份，从而削弱原有的节点冗余作用和破坏拓扑构建进程。在LEACH成簇过程中，Sybil攻击能在一定范围内影响网络的分簇，恶意节点自身和伪造的虚假节点都可自选为簇头，从而控制住整个簇，导致以恶意节点为中心的一定规模区域内合法节点的拓扑割裂。然而，ASCENT算法从概率的角度，以每个节点维持一定的邻居节点个数(连通度)来保证拓扑连通，通过链路质量来判断各节点的邻居关系。ASCENT算法能够较好地屏蔽Sybil攻击带来的不良影响，如果恶意节点和伪造节点不断地丢弃邻居节点的数据包，邻居节点必然在一定时间后识别出这种攻击，从而发出HELP包启动邻居节点的加入工作，维持拓扑连通。初步的单簇实验证实了Sybil攻击下ASCENT比LEACH有更强的适应性，前者的容侵能力优于后者。

在评估模型中，由上述分析，ASCENT进入入侵状态的概率pI值要小于LEACH中的值，而正常态的逗留时间 hN前者大于后者。不失一般性，取ASCENT和LEACH状态转换模型的pI分别为0.1和 0.4，hN分别为 13和 2，其余参数仍然利用 4.1节中的设置，得到的量化结果如图6所示。由图6可见，针对Sybil攻击，ASCENT在各个方面的拓扑容侵能力均优于 LEACH，特别是拓扑服务率显著优于LEACH，2个算法的定量比较结果与上述分析结果一致，验证了拓扑容侵能力量化评估模型的有效性。

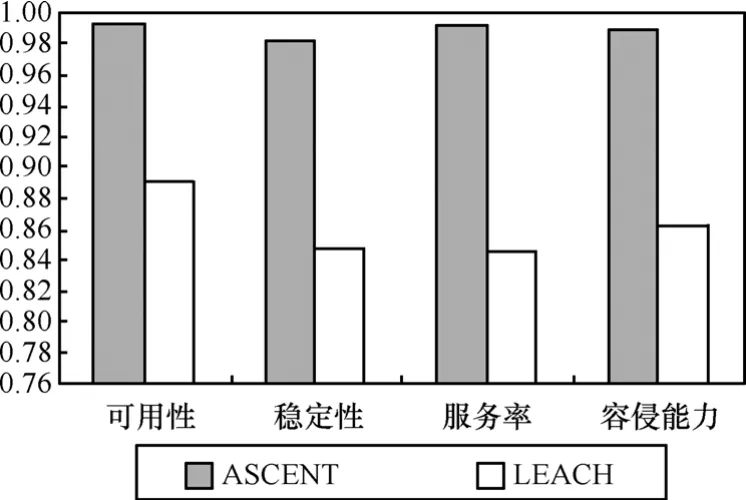
图6 Sybil攻击的ASCENT与LEACH容侵比较

4.3.2 Hello攻击的模型评估能力分析

针对LEACH发起Hello攻击的恶意节点会使用大功率无线设备广播Hello包，使得较大区域内的节点以较强的功率接收到该信息，都错误地加入以恶意节点为簇头的簇内，导致网络拓扑割裂。事实上，此时发生了链路非对称情况，部分节点的信号不可能到达恶意簇头。可见，LEACH协议对Hello攻击的容忍能力很差，极端情况拓扑完全割裂，整个网络不可用。ASCENT算法在Hello洪泛攻击威胁下，根据链路质量，节点i会错误地认为恶意节点是其一个合法邻居，降低了合法邻居个数，减弱了拓扑连通的服务能力。然而，这种影响是有限的，节点i仍然有k−1个合法邻居(k为从概率角度保持的邻节点个数)，仍然可以保持较好的连通性，对Hello攻击具有较强的容忍能力，初步测试验证了这一点。

在ASCENT和LEACH的拓扑容侵定量评估模型中参数pI分别取为0.1和0.4，hN分别为10和6，其余参数同Sybil分析，得到的定量比较结果如图7所示。针对Hello洪泛攻击，ASCENT在各方面均优于LEACH算法，量化比较结果与上述分析一致，验证了评估模型的有效性。

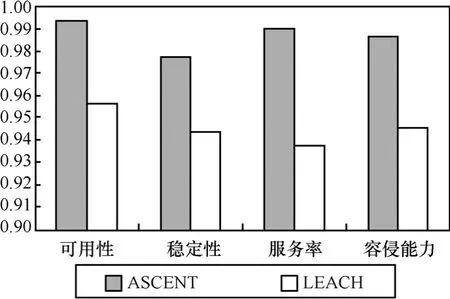
图7 Hello洪泛的ASCENT与LEACH容侵比较

5 相关工作比较分析

近年来，系统安全的定量评估开始受到研究人员的重视，本节针对采用不同评估技术的相关文献进行比较分析，表1给出了这些相关工作异同的对比。

Jonsson等[13]提出了一个基于攻击者行为的入侵定量分析模型，描述了入侵行为的3个阶段。鉴于入侵者之间攻击能力存在巨大差异，该模型定量评估每个攻击者的入侵能力十分困难。Albert等[6]针对复杂有线网络结构，用统计的方法分析了什么样的拓扑结构具有较高的容忍攻击能力。在基于SMP的安全系统定量评估研究中，较有影响的是Madana[8]提出的安全属性定量分析模型，该模型是一个通用模型，直接应用到拓扑容侵的定量评估中存在较多困难，且中间状态显得过于冗余，求解复杂。殷丽华等[14]提出了一个优化的容忍入侵系统状态转移模型，建立 SMP模型并对容侵系统安全属性进行定量分析。罗安安等[15]提出了一种针对TNC协议的基于半马尔可夫过程的评估模型，对可信网络连接的安全性进行量化分析。针对容侵系统的安全态势，秦华旺等[16]提出了一种基于入侵影响的评估方法，给出了数据机密度、完整度和可用度3个指标，得出了系统的安全态势，然而，该模型过于简单，不能准确描述系统的安全状态。WANG等[3]建立了传感器网络拓扑容侵能力的数学模型，对拓扑容侵能力进行了分析，但并未给出具体的容侵能力衡量指标。

本文将Madana[8]中基于SMP的建模方法用于研究WSN的拓扑容侵定量评估，提出了一个容侵拓扑构建的状态转移描述模型；同时，针对传感器网络节点资源受限的不足，精简中间状态，降低了节点资源开销，利于延长网络寿命。从 SMP模型中抽象出3个容侵能力衡量指标，再通过Bayes推理网络综合得出拓扑容侵能力，从而提高了模型描述能力。

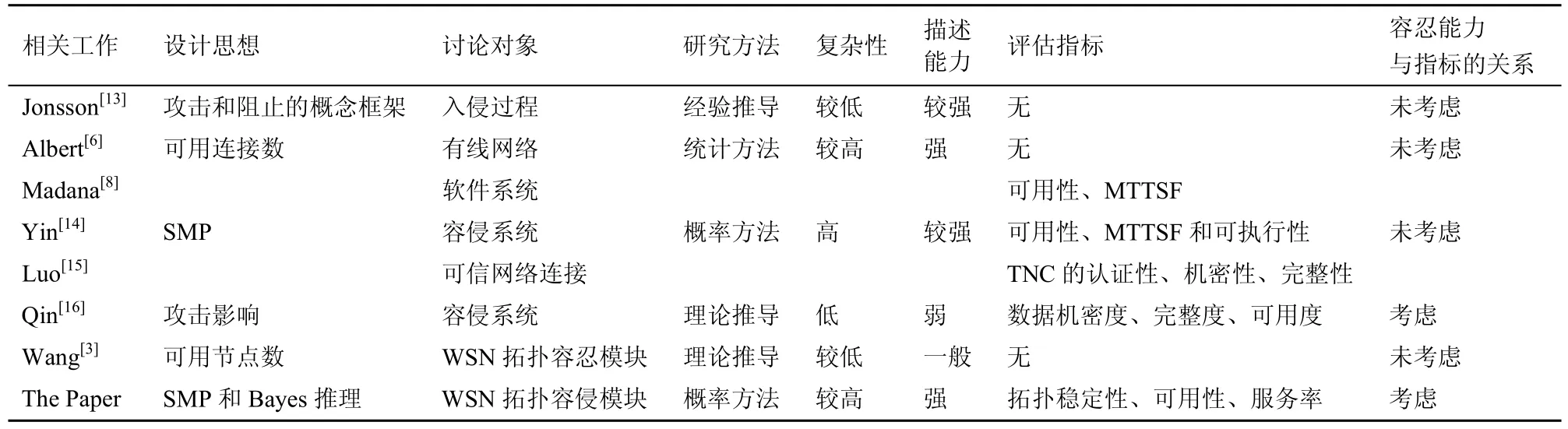
表1 相关工作比较

6 结束语

针对入侵行为影响，本文提出了拓扑容侵定量评估模型，以量化、分析拓扑的容侵能力。该模型采用半马尔可夫过程将拓扑构建过程划分为 6个状态，避免了对不同入侵威胁进行描述建模的复杂性，在入侵结果这个统一的层次上建模，简化了模型设计。利用内嵌DTMC模型求解容侵能力的各项指标，得出拓扑可用性、稳定性和服务率3个属性。通过贝叶斯推理网络，以新的样本值为后验信息，综合得出拓扑容侵能力；同时，不断改进 3个属性对整个拓扑容侵能力的贡献权重，从而提高容侵能力评估的准确性，便于传感器网络拓扑的重新配置。

仿真实验分析了评估模型对不同参数的敏感性，从而获得拓扑容侵技术的关键点，为选取合理的容侵拓扑更新机制提供了理论支持。对 LEACH和 ASCNT 2个拓扑构建算法进行了容侵能力剖析，验证了评估模型的有效性。下一步将研究具体的入侵检测模型，抽象出不同入侵行为对容侵模块的统一影响，从而准确提供模型工作参数。

[1]MOHSEN R, MOHAMMADTAGHI H, VAHAB S M.Fault-tolerant and 3-dimensional distributed topology control algorithms in wireless multi-hop networks[J].Wireless Networks, 2006, 12:179-188.

[2]JORGIC M, GOEL N, KALAICHEVAN K, et al.Localized detection of k-connectivity in wireless ad hoc actuator and sensor networks[A].Proc of the 16th IEEE International Conference on Computer Communications and Networks (ICCCN07)[C].Hawaii, 2007.33-38.

[3]王良民, 马建峰, 王超.无线传感器网络拓扑的容错度与容侵度[J].电子学报, 2006,34(8):1446-1451.WANG L M, MA J F, WANG C.Degree of fault-tolerance and intrusion-tolerance for topologies of wireless sensor networks[J].Acta Electronica Sinica, 2006, 34(8):1446-1451.

[4]MA R, XING L, MICHEL H E.Fault-intrusion tolerant techniques in wireless sensor networks[A].Proceedings of the 2nd IEEE International Symposium on Dependable, Autonomic and Secure Computing(DASC'06) [C].Indianapolis, 2006.85-94.

[5]王良民, 马建峰.基于再生技术的无线传感器网络容侵拓扑控制方法[J].计算机研究与发展, 2009, 46(10):1678-1685.WANG L M, MA J F.Self-regeneration based method for topology control with intrusion tolerance in wireless sensor networks[J].Journal of Computer Research and Development, 2009, 46(10):1678-1685.

[6]ALBERT R, JEONG H, BARABASI A L.Error and attack tolerance of complex networks[J].Nature, 2000, 406(27):378-382.

[7]裴庆祺, 沈玉龙, 马建峰.无线传感器网络安全技术综述[J].通信学报, 2007, 28(8):113-122.PEI Q Q, SHEN Y L, MA J F.Survey of wireless sensor network security techniques[J].Journal on Communications, 2007, 28(8):113-122.

[8]MADANA B B, POPSTOJANOVA K G, VAIDYANATHAN K, et al.A method for modeling and quantifying the security attributes of intrusion tolerant systems[J].Performance Evaluation, 2004, 56(1～4):167-186.

[9]TRIVEDI K S.Probability and Statistics with Reliability, Queuing,and Computer Science Applications[M].New York:Wiley Press,2001.

[10]刘东, 张春元, 邢维艳等.基于贝叶斯网络的多阶段系统可靠性分析模型[J].计算机学报, 2008,31(10):1814-1825.LIU D, ZHANG C Y, XING W Y, et al.Bayes networks based reliability analysis of phased-mission systems[J].Chinese Journal of Computers, 2008,31(10):1814-1825.

[11]HEINZELMAN W, CHANDRAKASAN A, BALAKRISHNAN H.Energy-efficient communication protocol for wireless microsensor networks[A].Proc of the 33rd Annual Hawaii Int’l Conf on System Sciences[C].Hawaii, USA, 2000.3005- 3014.

[12]CERPA A, ESTRIN D.ASCENT:adaptive self-configuring sensor networks topologies[J].IEEE Transactions on Mobile Computing,2004, 3(3):272-285.

[13]JONSSON E, OLOVSSON T.A quantitative model of the security intrusion process based on attacker behavior[J].IEEE Transactions on Software Engineering, 1997, 23 (4) :235-245.

[14]殷丽华,方滨兴.入侵容忍系统安全属性分析[J].计算机学报,2006,29(8):1505-1512.YIN L H, FANG B X.Security attributes analysis for intrusion tolerant systems[J].Chinese Journal of Computers, 2006, 29(8):1505-1512.

[15]罗安安, 林闯, 王元卓等.可信网络连接的安全量化分析与协议改进[J].计算机学报, 2009,32(5):887-898.LUO A A, LIN C, WANG Y Z, et al.Security quantifying method and enhanced mechanisms of TNC[J].Chinese Journal of Computers,2009,32(5):887-898.

[16]秦华旺,戴跃伟,王执铨.入侵容忍系统的安全态势评估[J].北京邮电大学学报, 2009,32(2):57-61.QIN H W, DAI Y W, WANG Z Q.Security situation evaluation of intrusion tolerant system[J].Journal of Beijing University of Posts and Telecommunications, 2009, 32(2):57-61.