Web 大数据系统数据源选择*

刘正涛，王建东

1.三江学院 计算机科学与工程学院，南京 210012

2.南京航空航天大学 计算机科学与技术学院，南京 210016

1 引言

在Web大数据系统中，一般包含大量的异构数据源，这些数据源将形成Web大数据系统的多个参与者，这些参与者在数据类型、数据元素的命名、数据的约束与限制等方面都是独立的，并且在操作执行与通信时，这些参与者也是独立的。为了能够同时访问多个Web数据源，Web数据集成系统必须对查询接口进行集成。当有了统一的访问接口后，如果只是把集成接口上的用户提交查询简单地转换成一个领域的每个Web数据源上的查询，显然是不可行的。因为这样操作存在以下问题：（1）查询花费的代价太高；（2）不是Web上每个数据源都能提供高质量的查询结果；（3）由于Web数据源返回结果之间存在大量冗余，查询的数据源数量越多，冗余度也会越大。基于以上原因，Web数据源选择成为Web大数据系统集成中的一个关键问题。把查询提交给很少量的数据源，但又要求返回的结果能够很好地满足用户的特定需求，是数据源选择的理想目标。针对不同的用户集成需求，Web数据源的选择方法各异。由于Web大数据集成系统需提供与查询相关且高质量的检索结果给用户，从而研究人员主要依据数据源与查询的相关性以及数据源本身质量来进行Web数据源选择的相关研究。

传统数据集成系统一般假定需要集成的数据源之间是相互独立的。然而，在处理一个查询所需要的大量Web数据源中，不同Web数据源中的数据存在着大量的重复记录，同时还存在着一些数据源从其他数据源拷贝了部分或全部数据的现象。数据源之间的数据相互覆盖与数据依赖将对数据源数据质量的评估、数据源排序及不同数据源的数据融合产生重要的影响。

本文主要目标是根据Web数据源的一些特征，从大量的数据源中选择k个质量适合并且与用户查询相关的数据源，以最少的时间代价满足用户的查询需求。本文的创新与贡献如下：

（1）提出了一个两阶段数据源选择方案。第一阶段通过各个数据源模式与中间模式的相似度选择与查询相关度高的数据源，通过计算依赖数据源的质量来选取质量较好的数据源；第二阶段基于最大熵理论计算数据源之间的重复率，选择查询效率最高的数据源。

（2）改进了ACCUNOD（accuracy of node）算法，在算法中加入了数据源之间依赖关系的考量，提出了一个新算法定义数据源的可信度。

（3）提出了最小代价查询模型，运用最大熵原理计算不同数据源之间的重复率，定义了一个最小代价查询优化算法。实验表明，与相关算法相比，该算法可以提高查询效率，具有一定的可扩展性。

本文组织结构如下：第2章对Web数据源选择与有数据重复的数据源的处理进行了分析与总结；第3章给出了Web大数据系统集成相关问题的一些基本定义；第4章给出了数据源模式与中间模式相似度的计算方法；第5章提出了有依赖关系的数据源可信度的计算方法；第6章提出了最小代价查询模型，并给出了运用最大熵原理计算数据源之间重复率的最小代价查询优化算法；第7章介绍了本文采用的实验方案，通过实验对提出的最小代价查询算法进行了评估，并对实验结果进行了分析；最后对全文进行总结，并给出今后的研究方向。

2 相关工作

Yu等人[1]提出了一种基于直方图的topN选择方法。该方法分为两步：第一步是判断数据库与特定查询之间的相关性；第二步是确定最适合提交查询的数据库和从返回的结果中选择最合适的记录。算法实验表明，这种计算topN查询的方法是非常有效的。可以使用本体技术对数据源的特征进行概念描述，同时提取查询的概念描述，计算相关性，进行数据源的选择。在Web数据源选择时，与用户查询相关的数据源质量参差不齐，数据源的质量是数据源选取的一个重要方面。Aboulnaga等人[2]设计了一个μBE（matching by example）数据集成系统，系统中使用了基于集成效用数据源选择方法。μBE系统根据三方面评价Web数据源质量：数据源模式在受约束条件下相互匹配程度、数据源中数据特征（覆盖度、冗余度、数据量）以及数据源自身的特征（延时、可靠性、费用、权威性）。μBE通过迭代一系列的受限优化问题来找出适合集成的数据源。Xian等人[3]提出了基于迭代的Web数据源选取和集成方法，该方法通过评价一个新加入数据源可能带来的增益来决定是否选取该数据源，其核心在于增益函数的设计。为了解决面向混合类型关键词查询的非合作结构化Deep Web数据源的选择问题，万常选等人[4]提出了一种属性与关键词结合的Deep Web数据源选择方法。该方法建立了特征词与主题词之间的关联性，特征词在约束型属性离散值上的记录分布直方图，以及两个特征词在同一约束型属性上直方图之间的约束相关性，对非合作结构化Deep Web数据源的约束型属性与检索型属性进行了有效的特征概括。Dong等人[5]平衡质量与花费，基于边际主义理论进行数据源选择。Rekatsinas等人[6]研究了动态数据源选择问题，基于数据源内容是随着时间而改变的，并定义了一组基于时效的评价集成数据质量的指标，如覆盖度、新鲜性、准确性等，因此数据源选择成为一个NP难问题，基于人工学习策略，给出了对应的近似解决策略。

在Web数据源选取时，数据源之间的数据重复是一个核心的问题。目前，有很多文献在数据选取时考虑了数据之间的重复或相交问题。Florescu等人[7]首先将数据源按照不同的领域进行分类，将每个数据源分成一个或多个领域中，然后利用概率信息来计算领域间的数据重复问题，并最终选择Top-k个数据源。StatMiner系统[8]在数据源排序时考虑了数据的重复问题。系统假定数据源与查询都可以标记为类层次，通过一些样本数据，计算不同类之间的重复问题，形成最佳的查询方案。文献[9-10]讨论了依赖数据源中的最小代价、最大覆盖率与数据源排序问题。Salloum等人[11]提出了一个OASIS（online query answering system for overlapping sources）系统，该系统使用最大熵原理动态统计数据源之间的重复率，实现了一个动态的在线数据源排序算法。

本文目标与以上文献的不同在于：

（1）对于一个查询q，本文目标是查询Top-k个元组，而不是全部元组；

（2）所选择的数据源必须满足一定的相关性与数据源质量要求；

（3）聚焦于能够获得最小查询代价。

3 相关定义

为了定义一个有依赖关系的Web大数据集成系统，给出了有关数据源、数据源的依赖关系等问题的形式化定义。

定义1（Web数据源）数据源为提供系统集成数据的来源，例如Deep Web数据站点、XML数据文件、关系数据库等。一组数据源可以表示为S={s1,s2,…,sn}，其中si(1≤i≤n)是第i个数据源。

定义2（实体）客观世界中一个独立存在事物的总称为一个实体。每个实体具有唯一的标识符。

定义3（实体属性）实体属性表示一个客观世界实体的特征的描述。一个实体的属性可以表示为A={a1,a2,…,an}，其中ai(1≤i≤n)为实体的第i个属性。实体的属性集合也被称为该实体的模式。例如，一本书的属性有ISBN号码、价格、作者等。

定义4（数据源依赖性DAG）通过一个DAG来表示Web数据源集合S={s1,s2,…,sn}之间的依赖性，其中对于每个数据源si∈S，对应着DAG中的每一个节点v；如果si依赖于sj，即si从sj拷贝了数据，则有一条有向边来表示二者的依赖状况，记作si→sj。

4 数据源模式匹配

在一个Web大数据系统中，一项重要的工作就是创建一个中间模式和建立中间模式与源数据模式之间的映射关系。这项工作需要理解数据源的数据结构，并了解用户将如何对数据进行查询。但这对于Web大数据系统来说是不可能实现的，必须通过自动的集成方法来实现模式集成。该全局集成模式包括来自不同数据源模式的属性集合，将该属性集合定义为全局属性（global attribute，GA）。同时，将所有数据源的模式与该全局属性集合建立属性之间的映射关系。一个良好的GA不能同时包含概念相同的两个属性。其定义如下：

定义5（良好GA）g是一个属性集合，g∈GA，{aij}是数据源模式属性与GA之间的映射，g是良好的当且仅当g≠∅并且

定义6（中间模式）中间模式M={g1,g2,…,gn}，其中gi∈M是良好的当且仅当

定义7（模式包含）中间模式M1包含中间模式

在模式映射相似度计算过程中，使用了多策略信息决策方法。使用的策略包括属性名称、实例与数据类型约束。对于以上3个决策预测结果采取了组合的方法进行合并[12]。

5 数据源可信度

数据源的可信度影响着数据值的准确程度，通常人们更愿意相信那些可信度比较高的数据源，就好像人们在向别人咨询消息一样，某些人可信程度较高，其提供的消息可信度就会很高，相反，有些人经常说一些谎言，可信程度比较低，其提供的信息可信度就会很低。数据源也一样，可信度越高的数据源它所提供的数据值的可信度也就越高。依据这一理论，数据源可信度将对数据值的正确性产生影响。因此，在选择数据源时，数据源的可信度是一个重要的指标。

针对数据源的可信度的求解，Yin等人[13]提出的ACCUNOD算法，该算法的基本思想是每一个数据源都有一个可信度，数据源的可信度影响数据信息可信度，而数据源的可信度又是根据它所提供的数据值的可信度决定的，因此数据源的可信度与数据值的可信度是相互影响的，利用迭代算法的思想去计算数据源的可信度和数据值的可信度。该算法没有考虑数据源相互依赖的情况。Dong等人[14-15]进一步考虑了数据源的准确性因素，并将其与数据源的依赖关系结合起来，获得了较好的效果。以上文献的出发点是通过计算数据源的可信度与依赖度来发现数据的可信度，本文的出发点主要是发现高可信度的数据源。

ACCU（accuracy）算法是在BENE（beneficial）算法和MAL（malice）算法的基础上提出的，该方法既考虑了数据源的依赖关系，也考虑了数据源的可信度。其基本计算方法如下。

当两个数据源si与sj相互独立时，即si⊥sj，根据概率公式有：

当数据源sj拷贝si时，即sj→si，根据概率公式有：

其中，Ot为数据源si与sj提供相同正确值的实体集合；Of为数据源si与sj提供不相同错误值的实体集合；Od为数据源si与sj提供不相同值的实体集合；ε(s)为数据源s提供错误值的概率；c为拷贝数据源拷贝数据比例。

对于数据源的可信度，可以使用以下公式来计算：

其中，m是数据源s提供的值的个数；V(s)是数据源s提供的数据值的集合；P(v)表示数据值v正确的概率。

P(v)可以通过以下公式来计算：

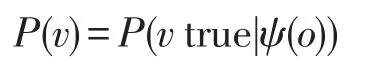
每个数据值的可信度C(v)为：

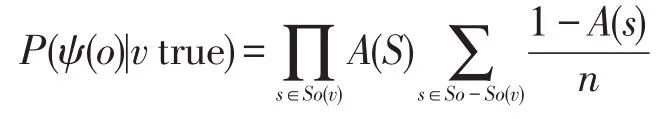
其中，I(s)为数据源s的选票数。

通过以上分析可以得知：数据源的可信度依赖于每个数据源中数据值的准确度；数据源之间的依赖性依赖于数据源中数据值的准确度与数据源的可信度；而数据值的准确度依赖于数据源的准确度以及与其他数据源之间的依赖关系。下面通过算法1的迭代得出各个数据源的准确度。

算法1给出了每个数据源可信度的计算方法，其基本思想为：首先给定每个数据源s的初始可信度为1-ε，然后通过迭代的方法求出每个数据源的可信度A(s)。其基本方法为：计算数据源相互之间的依赖概率，按照依赖概率对数据源进行排序，计算每个数据对象各属性的可信度，计算数据源的可信度。直到每个数据源s的准确度A(s)变化小于某个值，并且需要确定的正确值集合无振荡时结束循环。

算法1ACCU_VOTE

输入：数据源集合S，数据源数据的值集合O。

输出：每个数据源的可信度。

//每个数据源s的准确度A(s)变化小于某个值，并且需要确定的正确值集合无振荡时结束循环

6 最小代价查询算法

在Web大数据系统中，各数据源的访问时间各异，数据源之间的重复情况不同，为了减少访问时间，其关键问题在于各数据源的访问顺序。

定义8（代价）s为一个数据源，q是一个查询。查询数据源s的代价为C(s)=CC(s)+TC(s)×|q(s)|。其中，CC(s)为数据源s的连接时间；TC(s)为数据源s每个元组的传输时间；|q(s)|为查询返回的元组总数。

定义9（查询效率）一个数据源的查询效率为vi=C(s)/|q(s)|，即查询总体代价与所查询的元组总数之比。

定义10（最小代价模型（time-cost minimization model，TMM））给定一个查询qi，一个数据源集合S={s1,s2,…,sn}，需要查询k个元组，找到一个数据源的排列序列Πopt{1,2,…,k}，使得其他任何排列Π都有C(qi(Πopt(S)))≤C(qi(Π(S)))。

例1不存在交叉。给定3个数据源s1、s2、s3，为简便起见，CC(s1)=CC(s2)=CC(s3)=0，3个数据源的每个元组传输时间分别为TC(s1)=0.8 ms，TC(s2)=1.0 ms，TC(s3)=1.6 ms。对于一个查询q，通过统计得知|q(s1)|=50，|q(s2)|=150，|q(s3)|=80，3个数据源的元组交叉情况为|q(s1)∩q(s2)|=0，|q(s1)∩q(s3)|=0，|q(s2)∩q(s3)|=0，|q(s1)∩q(s2)∩q(s3)|=0。也就是说，3个数据源相互独立并且不存在交叉情况。可以得出以下结论：

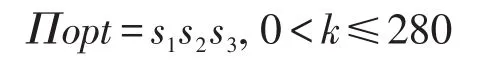
例2存在交叉。给定3个数据源s1、s2、s3，为简便起见，CC(s1)=CC(s2)=CC(s3)=0，3个数据源的每个元组传输时间分别为TC(s1)=0.8 ms，TC(s2)=1.0 ms，TC(s3)=1.6 ms。对于一个查询q，通过统计得知|q(s1)|=50，|q(s2)|=150，|q(s3)|=80，3个数据源的元组交叉情况为|q(s1)∩q(s2)|=25，|q(s1)∩q(s3)|=10，|q(s2)∩q(s3)|=15，|q(s1)∩q(s2)∩q(s3)|=0。也就是说，3个数据源互相之间存在交叉情况。可以得出以下结论：

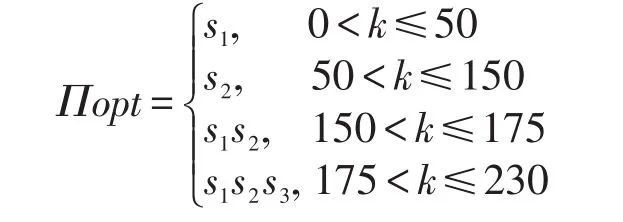
通过两个例子，可以得出以下两个观察：

观察1如果所选择的数据源中不存在查询结果交叉问题，则最小查询代价模型可以得到查询的最优结果。

观察2如果所选择的数据源中存在查询结果交叉问题，则最小查询代价模型需要考虑查询数据源的查询效率与数据源之间的数据重复情况。

在实践中，可以观察到一些小型网站经常引用或拷贝大型网站的数据，与大型网站的数据重复率很高，因此可以得到以下观察。

观察3数据数量少的数据源经常拷贝或引用数据数量比较大的数据源，在查询时，数据数量较大的数据源应赋予更高的优先级。

查询效率贪婪算法（MinC）的核心思想：每次在待查询的数据源集合中寻找一个最大效率的，直到查询的元组大于等于k个元组或者所有的数据源都已经查询完毕。该算法对于没有重复的数据源可以得到最高的查询效率。

算法2查询效率贪婪算法（MinC）

输入：一个查询q，所需要查询的元组数k，一个待查询的数据源集合S，数据源集合的查询效率V。

输出：数据源优化序列Πopt。

数据源最大数量贪婪算法（MaxT）的核心思想是：每次在待查询的数据源集合中寻找一个最大数据量的数据源，直到查询的元组大于等于k个元组或者所有的数据源都已经查询完毕。MaxT算法与MinC算法的步骤基本一致，MaxT算法优先选择元组数目大的数据源。

算法3数据源最大数量贪婪算法（MaxT）

输入：一个查询q，所需要查询的元组数k，一个待查询的数据源集合S，数据源集合的元组数集合|S|。

输出：数据源优化序列Πopt。

根据观察2，优化排序算法（Optimization）优先选择一个数据数量最大的数据源作为第一个数据源，然后根据已选择数据源Πopt与待选数据源集合S的重复情况，优先选择最大效率的数据源加入到Πopt队列中，直到查询的元组大于等于k个元组或者所有的数据源都已经查询完毕。

为了估算Πopt队列集合与剩余数据源集合S中的每个数据源s的重复率，应用最大熵原理来实现重复率的估算问题。

其中，V(Ω)为重复估计时的可能变量，使用了文献[11]中的重复估计算法。

算法4优化排序算法（Optimization）

输入：一个查询q，所需要查询的元组数k，一个待查询的数据源集合S，数据源集合的查询效率V。输出：优化序列Πopt。

在实际的Web大数据集成系统中，数据源的选择通常需要两个阶段：第一个阶段是数据质量的评估以及查询与数据源的相关性计算，选择合适质量与一定查询相关性的数据源；第二阶段使用最小查询代价模型算法给数据源进行排序。在排序时，如果用户对查询的相关性与质量有特殊需求，可以在第二阶段算法中加入模式相关性与质量的影响因子。

7 实验评估

7.1 实验设计

为了评估算法的执行情况，本文搭建了一个模拟实验平台。首先，使用网络爬虫从不同的Web站点寻找了1 500个有关书籍的站点，然后通过算法1对每一个数据源的总体质量进行计算。1 500个网站的数据总共记录数为241 660条，在这些记录中，总共有25 320条不同的书目。为了简化计算以及减少网络因素的影响，首先对各个站点的访问代价CC(s)、每个元组的传输时间TC(s)进行统计，然后收集每个站点的所有元组，经过一定的语义转换，放到一个MySQL关系数据库里面。为了进行评估，实现了4个算法。

（1）随机算法（Random）：通过随机方法，任意选择下一个数据源进行排序；

（2）最大元组法（MaxT）：不考虑数据源之间的覆盖问题，每次直接选择当前队列中的最大|q(s)|数的数据源s，进行数据源排序；

（3）最小代价算法（MinC）：不考虑数据源之间的覆盖问题，每次直接选择每个元组最小代价的数据源s，进行数据源排序；

（4）优化算法（Optimization）：根据算法4，在选择数据源时，应用最大熵原理，动态计算待选数据源s与已经建立的队列的重复情况，选择最佳的数据源。

系统原型：使用Java语言实现了一个包括以上4个算法的数据集成系统实验平台。实验平台的操作系统为MS-Windows7，CPU为i54460，8 GB内存，所有的查询都在同一个网络中进行，实验共使用了两台计算机，一台用于数据存储，一台用于计算数据。

实验参数设计：

（1）第一组实验主要针对本文提出的4个算法进行了比较，共完成了3个实验。第一个实验测试4个算法在不同Top-k下的性能表现，分别将k的取值设为数据源不同数据总数的0.1、0.2、0.5、0.8。该实验目的是测试不同算法在用户需求数据数量不同时的表现。第二个实验测试4个算法在不同数据源数目情况下的执行效率，该实验k的取值为0.3，数据源的数据各选取500个、1 000个、1 500个，其中数据源的选择采取了随机选取的办法。第三个实验测试优化算法在使用多线程技术情况下的执行效率，该实验中k的取值为0.3。

（2）第二组实验主要对优化算法与文献[11]中的DYNAMIC+算法进行比较，共完成了两个实验。第一个实验测试完整优化算法与DYNAMIC+算法的性能，实验中k的取值为0.3（共计7 600条不同记录）、0.6（共计14 200条不同记录）。第二个实验两个算法使用的数据源相同，都是经过第一阶段预处理过的数据源，数据源总数为1 000个，实验中k的取值为0.3（共计7 600条不同记录）、0.5（共计10 400条不同记录）。在两组实验中，各种算法都分别执行了100次，最后的取值为100次实验结果的平均值。

7.2 实验分析

7.2.1 第一组实验

Fig.1 Response time of algorithms with different proportion of tuple图1 不同返回元组数的查询响应时间

第一个实验的结果如图1所示。通过实验可以得知：不管k的取值大小，总体来说，Random算法的执行时间最长，效率最低，MaxT算法的执行时间比Random算法要少，MinC算法相对MaxT算法的效率有所提升，Optimization算法执行时间最少，相对其他算法有较大的提升；当k=0.1时，Random算法、MaxT算法、MinC算法、Optimization算法的执行时间分别为16.3、14.2、7.1、5.1 s；当k=0.8时，4个算法的执行时间分别为241.5、211.3、114.5、86.1 s。由图1可以明显看出，当k值增加时，Random算法增加的幅度最大，Optimization算法增加的幅度最小。

第二个实验的结果如图2所示。通过实验可以得知：（1）随着数据源数目的增多，各个算法的时间都有增加，但不管|S|取值大小，Optimization算法都是同等条件下最优的。（2）当数据源数目增加时，不同算法时间增加的幅度不同，其中Random算法增加的比例最大，当|S|=500时，CRandom=15.8 s；当|S|=1 000时，CRandom=71.4 s；时间增加了452%，与此同时，Optimization算法的访问时间增加了252%。（3）Optimization算法随着数据源的增加，访问时间线性增加，算法具有一定的扩展性。

Fig.2 Response time of algorithms with different number of sources图2 不同数据源个数的查询响应时间

第三个实验主要测试在多线程并行计算下4个算法的执行效率，实验中k的取值为0.3，数据源数量为1 000个，实验分别测试了1～12个线程的执行效率。实验结果如图3所示。通过实验可以得知：（1）线程数量越多，各种算法的查询执行时间都在减少，线程增加时，执行时间的降低并非线性降低。（2）当线程数量小于5开始，时间的减少比较明显；当线程数量大于5时，时间减少速度开始明显趋缓。

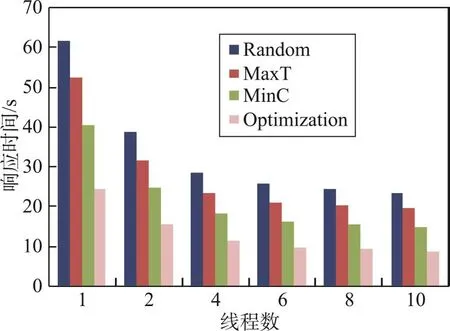
Fig.3 Response time of algorithms with Parallel query answering图3 并行查询各算法查询时间

7.2.2 第二组实验

第二组实验主要比较Optimization算法与文献[11]DYNAMIC+算法性能，测试中分别使用了单线程模式与并行模式。

在第一个实验中，Optimization算法使用的数据源是经过第一阶段排序过的数据源，DYNAMIC+算法使用的是随机选择的数据源。测试结果如图4所示。通过实验结果可以得知：（1）数据源数量越少，Optimization算法相对DYNAMIC+算法的性能越好。（2）Optimization算法总体来说性能比DYNAMIC+算法要好一些。（3）采用单线程模式与多线程模式对于趋势的影响不大，主要原因就是Optimization算法使用的数据源经过了第一阶段数据质量的评估。经过统计表明，质量高的数据源的响应时间往往比较小。当数据源数量较少时，根据第一阶段的数据源选择策略，从总体的数据源中选取了比较好的一些数据源，相应的执行效率就比较高；当数据源数量增多时，这种优势就会降低，两个算法的性能就会慢慢接近。

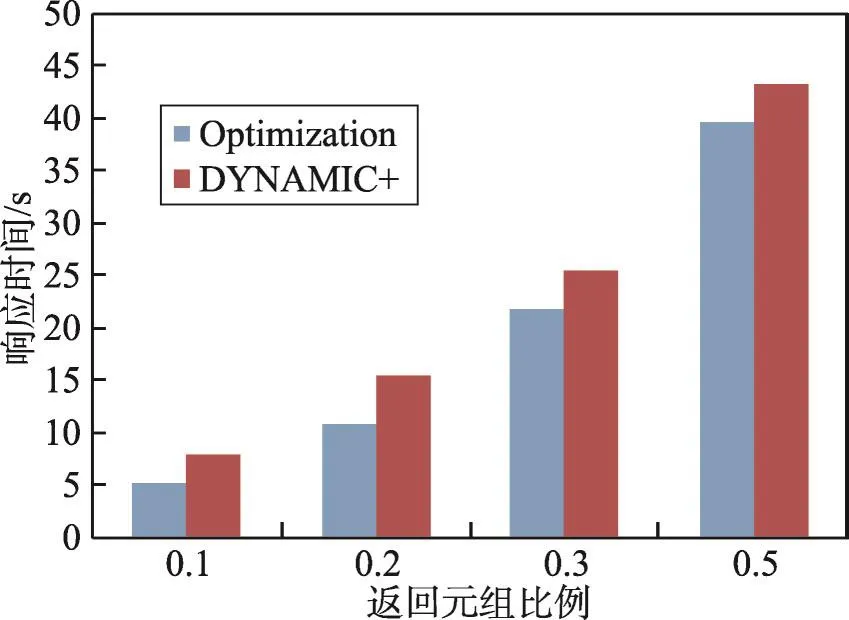
Fig.4 Performance comparison of optimization algorithm and DYNAMIC+algorithm图4 覆盖优化算法与DYNAMIC+性能比较

图5给出第二个实验的测试结果。通过实验结果可以得知：（1）两个算法的性能基本相当。（2）当查询数据数量比较少时，DYNAMIC+算法性能更好一些；当查询数据数量较多时，Optimization算法性能更好一些。

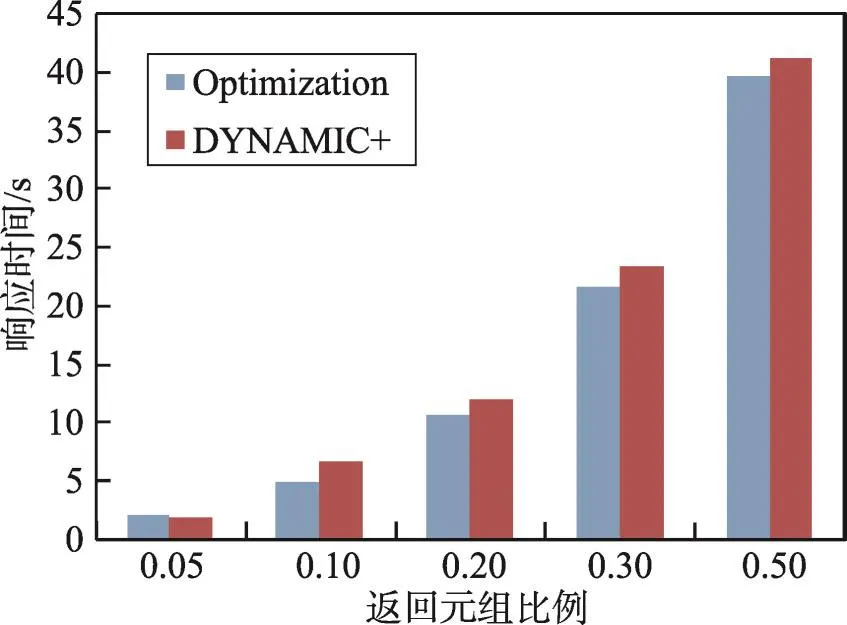
Fig.5 Performance comparison of optimization algorithm and DYNAMIC+algorithm图5 覆盖优化算法与DYNAMIC+性能比较

实验小结：（1）第一组实验表明，在同等条件下，Optimization算法比其他算法的性能更好；同时，Optimization算法具有一定的扩展性。（2）第二组实验表明，与相关算法DYNAMIC+相比，Optimization算法总体上来说性能更优。

8 结束语

数据源的选择与排序是Web大数据系统的关键问题之一。数据源之间的重复是选择数据源的关键问题。本文提出了一个两阶段数据源选择排序方法：第一阶段通过组合的方法计算查询与数据源之间的相关性，通过计算数据源的可信度计算数据源的质量，在计算数据源质量时考虑了数据源之间的重复情况。在第一阶段选择了与查询具有一定相关度与质量标准的数据源。第二阶段设计了4个算法，随机算法、最大元组法、最小查询代价算法、优化算法。4个算法各有不同的应用场景，通过该系列算法对第一阶段选择的数据源进行排序。实验结果表明，与相关算法相比，Optimization算法可以减少系统查询时间，具有一定的扩展性。下一步的工作是结合并行算法对目前的最小代价查询算法进行进一步的优化。

[1]Yu C,Philip G,Meng Weiyi.Distributed top-Nquery processing with possibly uncooperative local systems[C]//Proceedings of the 29th International Conference on Very Large Data Bases,Berlin,Sep 9-12,2003.San Mateo:Morgan Kaufmann,2003:117-128.

[2]Aboulnaga A,El Gebaly K.μBE:user guided source selection and schema mediation for internet scale data integration[C]//Proceedings of the 23rd International Conference on Data Engineering,Istanbul,Apr 15-20,2007.Washington:IEEE Computer Society,2007:186-195.

[3]Xian Xuefeng,Zhao Pengpeng,Yang Yuanfeng,et al.Efficient selection and integration of hidden Web database[J].Journal of Computers,2010,5(4):500-507.

[4]Wan Changxuan,Deng Song,Liu Dexi,et al.Non-cooperative structured deep Web selection based on hybrid type keyword retrieval[J].Journal of Computer Research and Development,2014,51(4):905-917.

[5]Dong X L,Saha B,Srivastava D.Less is more:selecting sources wisely for integration[J].Proceedings of the VLDB Endowment,2012,6(2):37-48.

[6]Rekatsinas T,Dong X L,Srivastava D.Characterizing and selecting fresh data sources[C]//Proceedings of the 2014 International Conference on Management of Data,Snowbird,Jun 22-27,2014.New York:ACM,2014:919-930.

[7]Florescu D,Koller D,Levy A Y.Using probabilistic information in data integration[C]//Proceedings of the 23rd International Conference on Very Large Data Bases,Athens,Aug 25-29,1997.San Francisco:Morgan Kaufmann Publishers Inc,1997:216-225.

[8]Nie Zaiqing,Kambhampati S,Nambiar U.Effectively mining and using coverage and overlap statistics for data integra-tion[J].IEEE Transactions on Knowledge and Data Engineering,2005,17(5):638-651.

[9]Sarma A D,Dong X L,Halevy A Y.Data integration with dependent sources[C]//Proceedings of the 14th International Conference on Extending Database Technology,Uppsala,Mar 21-24,2011.New York:ACM,2011:401-412.

[10]Liu Xuan,Dong X L,Ooi B C,et al.Online data fusion[J].Proceedings of the VLDB Endowment,2011,4(11):932-943.

[11]Salloum M,Dong X L,Srivastava D,et al.Online ordering of overlapping data sources[J].Proceedings of the VLDB Endowment,2013,7(3):133-144.

[12]Liu Zhengtao,Wang Jiandong.Pay-as-you-go schema integration in Web dataspace[J].Journal of Frontiers of Computer Science and Technology,2011,5(1):87-96.

[13]Yin Xiaoxin,Han Jiawei,Yu P S.Truth discovery with multiple conflicting information providers on the Web[J].IEEE Transactions on Knowledge&Data Engineering,2008,20(6):796-808.

[14]Dong X L,Berti-Equille L,Srivastava D.Integrating conflicting data:the role of source dependence[J].Proceedings of the VLDB Endowment,2009,2(1):550-561.

[15]Dong X L,Berti-Equille L,Srivastava D.Truth discovery and copying detection in a dynamic world[J].Proceedings of the VLDB Endowment,2009,2(1):562-573.

附中文参考文献：

[4]万常选,邓松,刘德喜,等.面向混合类型关键词查询的非合作结构化深网数据源选择[J].计算机研究与发展,2014,51(4):905-917.

[12]刘正涛,王建东.Web数据空间边建边用模式集成[J].计算机科学与探索,2011,5(1):87-96.