有界滯量脉冲泛函微分系统零解的指数稳定性＊

王华丽,褚玉明,符海龙

(1.厦门大学数学科学学院,福建厦门361005; 2.湖州师范学院理学院,浙江湖州313000;3.浙江大学附属中学,浙江杭州310007)

有界滯量脉冲泛函微分系统零解的指数稳定性＊

王华丽,褚玉明,符海龙

(1.厦门大学数学科学学院,福建厦门361005; 2.湖州师范学院理学院,浙江湖州313000;3.浙江大学附属中学,浙江杭州310007)

利用Halanay微分不等式建立了Dini导数微分不等式,并证明了有界滞量的脉冲泛函微分系统的零解是全局指数稳定的.

Halanay不等式;脉冲泛函微分系统;指数稳定性

MSC 2000:34K20 34K38

近年来,脉冲泛函微分系统已被广泛应用于神经网络、光学控制、人口动力学、生物技术、经济学等领域,对这类系统解的性质研究已经成为许多数学工作者的热门研究课题[1～3].稳定性理论已经取得了许多成果,其中研究指数稳定性主要是利用Lyapunov函数方法和Razumikhin技巧[5].众所周知,微分不等式在微分系统的定性和定量理论研究中起到了非常重要的作用[1,3,4],其中Halanay不等式是一个典型的例子.本文首先将Halanay微分不等式推广到Dini导数微分不等式,并用它研究有界滞量滞后型脉冲泛函微分系统的指数稳定性.

1 预备知识

考虑如下的脉冲泛函微分系统

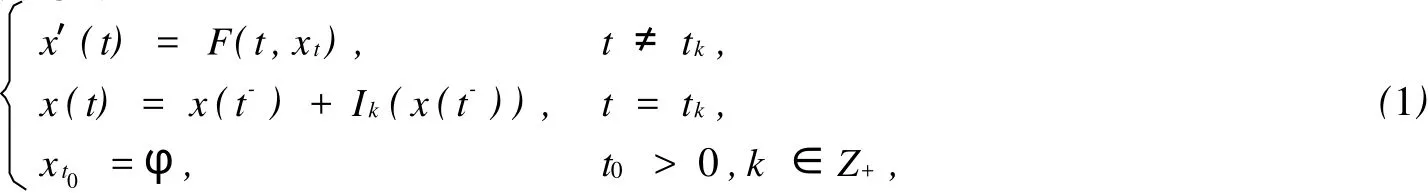
其中Z+是全体正整数集合,xt脉冲时刻tk满足0tk=+∞,x′(t)表示x在t处的右导数.F(t,xt)∈C([tk-1,tk)×Cn,Rn),F(t,0)=0.Ik(t,x)∈C(R× PC([-τ,0],Rn),Rn),Ik(t,0)=0,k∈Z+.PC(I,Rn)={ψ∶I→Rn|ψ是除去点列tk的连续函数,在t =tk∈I处,ψ都存在,且ψ=ψ(tk),其中I表示R上的一个区间;Cn={ψ:ψ∈PC([-τ, 0],Rn)}.我们总假设F(t,ψ),Ik满足适当的条件以保证系统(1)解的整体存在性和唯一性[6～7].

定义1 称函数V∶[0,∞)×Rn→R+是v0函数类,若满足: (i)V在[tk-1,tk)×Rn上连续,V(t,y)=V存在; (ii)V(t,x)关于x满足局部Lispschitz条件且V(t,0)≡0.

定义2 对V∈v0,对任意(t,x)∈[tk-1,tk)×Rn,V(t,x)沿系统(1)的Dini右上导数定义为:

定义3 设x(t)=x(t,t0,φ)是系统(1)经过(t0,φ)的任一解,称系统(1)的零解是全局指数稳定的:若存在常数λ使得对任意的初始条件(t0,φ),有

2 主要结果

首先建立一维脉冲时滞Halanay不等式,然后利用该不等式研究脉冲泛函微分系统(1)零解的指数稳定性.

引理1(Generalized Halanay Inequality) 假设存在函数m(t)∈PC([t0-τ,∞),R+)满足:

(i)t=tk时,m(tk),其中γk>0;

(ii)t≥t0,t≠tk时,

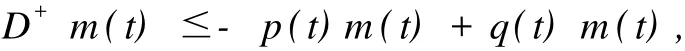
则有

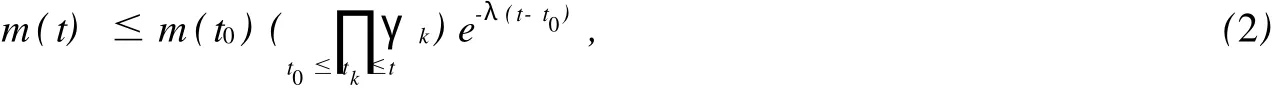
其中λ满足0<λ<μ＊, μ＊∶μ(t)-p(t)+rq(t)eμ(t)τ=0}.

证明 首先证明μ＊存在且μ＊>0.令

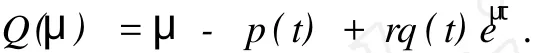
由于Q(0)=-p(t)+rq(t)<0,Q′(μ)=1+rτq(t)eμτ>0,Q(+∞)>0,所以Q(μ)是严格单调递增的.故对给定的t≥t0存在唯一的正函数μ(t)>0,使得

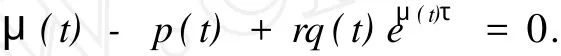
由μ＊的定义可知μ＊≥0.下面证明μ＊>0.

反证,若不然,取充分小的ϵ>0,则存在t＊≥t0,使得

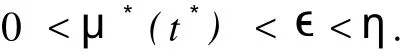
当x>0充分小时,不等式ex<1+1.5 x成立,从而有

得出矛盾!故μ＊>0,且存在λ,使得0<λ<μ＊.

下面证明不等式(2)成立.

首先,显然对t∈[t0-τ,t0]有:

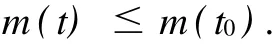
当t∈[t0,t1)时,只需证明:

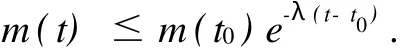
反证.若不然,则存在t∈[t0,t1),使得m(t)>.为方便起见,记

则显然有t＊∈[t0,t1)且

(1a)m(t＊)=w0(t＊);

(2a)m(t)≤w0(t),t∈[t0,t＊];

(3a)对任意δ>0,存在tδ∈(t＊,t＊+δ0),使得m(tδ)>w0(tδ),从而有

根据条件(ii),

再由条件(i)可以得到

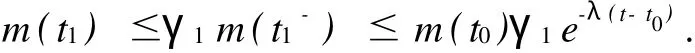
下面证明当t∈[t1,t2)时,(2)成立,即证

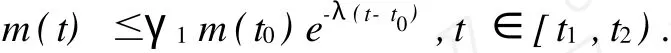
仍然采用反证法.否则,存在

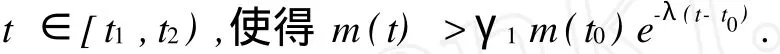
令

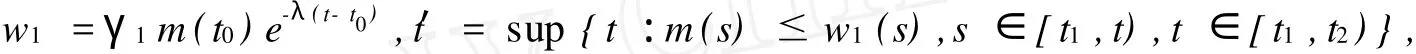
显然有t′∈[t1,t2)且

(1b)m(t′)=w1(t′);

(2b)m(t)≤w1(t),t∈[t1,t′];

(3b)对任意δ′>0,存在tδ′∈(t′,t′+δ′),使得m(tδ′)>w1(tδ′),从而有

考虑到条件(ii)、(iii)及(2b)得:

这与式子(4)矛盾!故对任意的t∈[t1,t2),(2)式成立.再利用条件(i)可知t=t2时,

进一步可以证明:

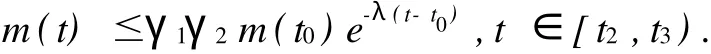
采用同样的方法,类似的定义w2,t″加以证明即可.

一般地,由归纳法,可以证得对t∈[tm,tm+1),m≥0有:

推论1 假设存在函数m(t)∈PC([t0-τ,∞),R+)满足:

(i)t=tk时,m(tk),其中γk>0;

(ii)t≥t0,t≠tk时,

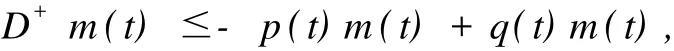
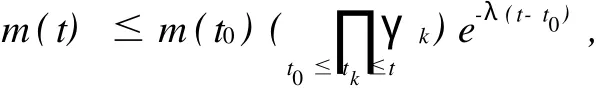
其中λ满足

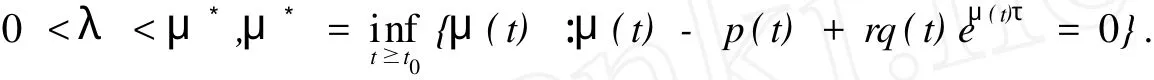
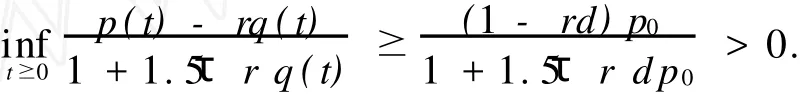
注1:如果γk≥1对所有的k∈Z+都成立,则可以去掉条件(iii).

注2:若m(tk)=m(tk-),则引理1的结果退化为文献[8]中的引理2.1;进一步,若有p(t)≡α>q(t)≡β>0,则成为文献[4]中的Halanay不等式.

定理1 假设

(ii)对任意的ψ∈PC([-τ,0],Rn),t=tk时,

其中βk

(iii)t≥t0,t≠tk时,有

则系统(1)的零解是全局指数稳定的.

证明 对任意的ϵ>0,t0>0,取

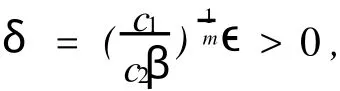
利用引理1和条件(i)有:

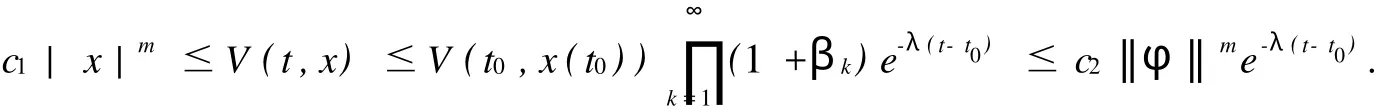
因此

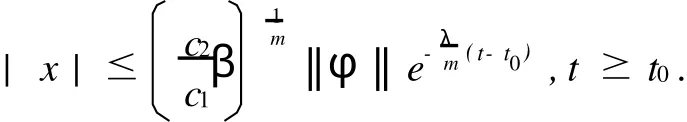
由于c2>c1,β>1,所以由定义3可知系统(1)的零解是全局指数稳定的.

[1]LA KSHM IKANTHAM V,LEELA S.Differential and Integral Inequalities[M].New York:Academic p ress,1969:37～43.

[2]HALE J K.Theo ry of Functional Differential Equations[M].Berlin:Sp ringer-Verlag,1977:106～130.

[3]LA KSHM IKANTHAM V,BA INOV D D,SIM EONOV P S.Theory of Impulsive Differential Equations[M].Wo rld Scientific:Singapore,1989:32～41.

[4]HALANAY A.Differential Equations,Stability,Oscillation,Timelags[M].New York:Academic Press,1996:7～130.

[5]STAMOVA IM,STAMOV G T.Lyapunov-Razumikhin method for impulsive functional differential equations and app lications to the population dynamics[J].Journal of Computation and Applied Mathematics,2001,130:163～171.

[6]BALL INGER G,L IU X Z.Existence,uniqueness and boundedness results for impulsive delay differential equations [J].App licable Analysis,2000,74:71～93.

[7]BALL INGER G,L IU X.Existence and uniqueness results for impulsive delay differential equations[J].Dynamics of Continuous,Discrete and Impulsive System s,1999,5:579～591.

[8]JIANGM,SHEN Y,L IAO X.On the global exponential stability fo r functional differential equations[J].Communications in Nonlinear Science and Numerical Simulation,2005,10:705～713.

Abstract:We establish an Dini derivative differential inequality by uesof the Halanay differential inequality and p rove that the zero solutions of the impulsive functional differential system sw ith bounded delay are globally exponential stable.

Key words:Halanay inequality;Impulsive functional differential system s;Exponential stability

MSC 2000:34K20 34K38

The Exponential Stability of Zero Solutions for Im pulsive Functional D ifferen tial Systems with Bounded Delay

WANG Hua-li1,CHU Yu-ming2,FU Hai-long3
(1.School of Mathematical Sciences,Xiamen University,Xiamen 361005,China; 2.Faculty of Science,Huzhou Teachers College,Huzhou 31300,China; 3.The High School A ttached to Zhejiang University,Hangzhou 310007,China)

O175.21

A

1009-1734(2010)02-0013-05

2010-03-20

王华丽,厦门大学数学科学学院2010级博士生,从事动力系统和微分方程研究.