高收敛阶采样定理的构造

谢长珍，陈桂章

（汕头大学数学系, 广东 汕头 515063）

高收敛阶采样定理的构造

谢长珍，陈桂章

（汕头大学数学系, 广东 汕头 515063）

基于过采样技术，对Shannon采样定理进行了改进，得到高逼近阶采样定理，提升了其收敛速度.

Shannon采样定理；过采样；收敛阶

0 引 言

香农（Shannon）采样定理，又称奈奎斯特采样定理，是信息论、特别是通讯与信号处理学科中的一个重要基本定理，在信号处理中有着十分重要的地位，是数字信号转化为模拟信号的理论基础.采样是将一个信号（即时间或空间上的连续函数）转换成一个数值序列（即时间或空间上的离散函数）.香农采样定理指出，如果信号是带限的，并且采样频率高于信号带宽的一倍，那么，原来的连续信号可以从采样样本中完全重建出来[1].从信号处理的角度来看，采样定理描述了两个过程：其一是采样，这一过程将连续时间信号转换为离散时间信号；其二是信号的重建，这一过程离散信号还原成连续信号.众所周知，Shannon采样定理在重构信号时收敛速度很慢，影响了它在实际工作中的应用.为了提升其收敛速度，Walter[2]首先将Shannon采样定理推广到小波子空间，得到了小波子空间上的采样定理.王旭、邓彩霞和朱建立[3]从线性变换的角度出发，结合再生核Hilbert空间中再生核函数的特殊性质，建立了再生核Hilbert空间中函数的采样定理.Liu Youming等人[4]构造出一类带限基插值小波，其对应的尺度函数具有Shannon尺度函数类似的性质，如频带有限性、平移正交性和插值性等.更多有关采样定理的研究见文献［5-7］.Boggess等人[8]采用过采样技术，得到了过采样定理，且增加了它的收敛速度.基于过采样思想，本文对Shannon采样定理做了进一步研究，得到新的采样算法，其收敛速度高于文献［8］中采样定理的收敛速度.

1 采样定理的构造

首先介绍本文使用的一些记号，e表示自然对数的底，i表示虚数单位；j，n均表示整数.

引理1[1]设是分段光滑且连续的带限信号，即其中Ω是正数.则， 其中为常数.

引理2[1]设f（λ）是分段光滑且连续的带限信号，即Suppf⊆[-Ω，Ω]，其中Ω是正数.那么 f（t）可以由其离散采样点 tj=jπ /Ω， j=0，± 1，± 2，…处的值精确重构.即 f可以精确地表示为如下形式：

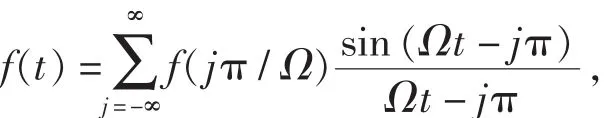
且上面的级数是一致收敛的.

从引理2可以看到，其系数绝对值的衰减率只为1/j，重构f（t）的收敛速度比较慢.为了提高收敛速度，文献［3］给出了下面的过采样定理.

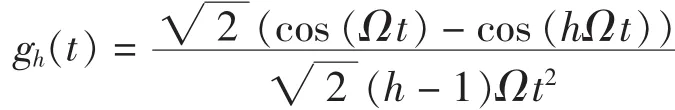
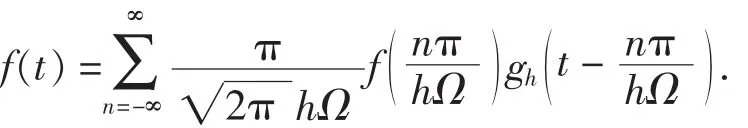
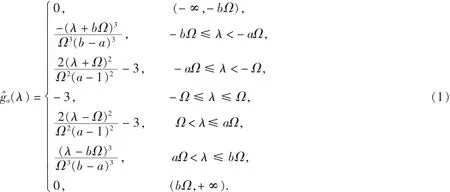
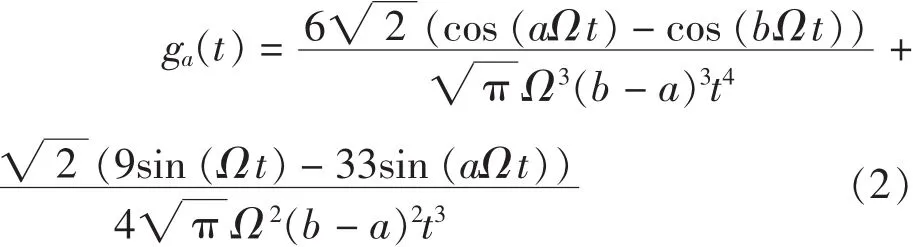
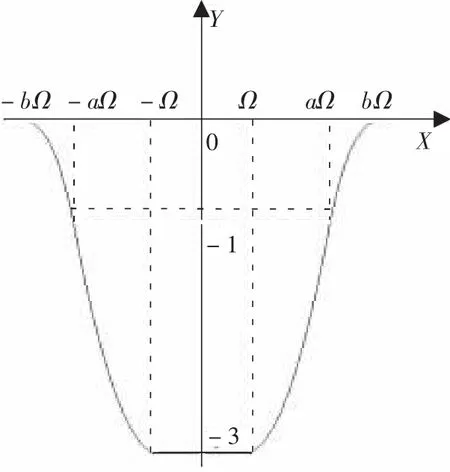
图1 a（λ）的图形

证明 下面分四步来计算

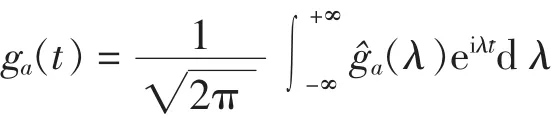
的值.

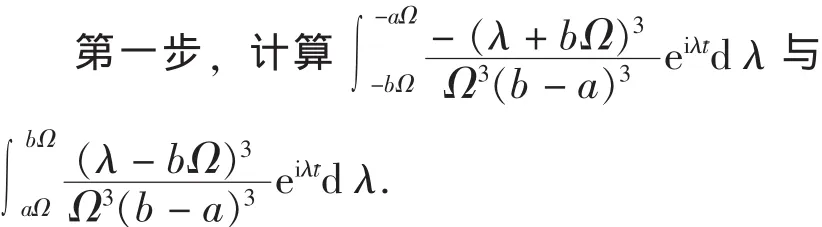
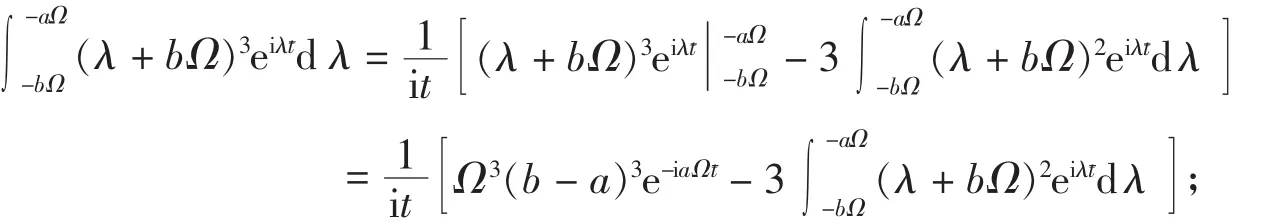
而

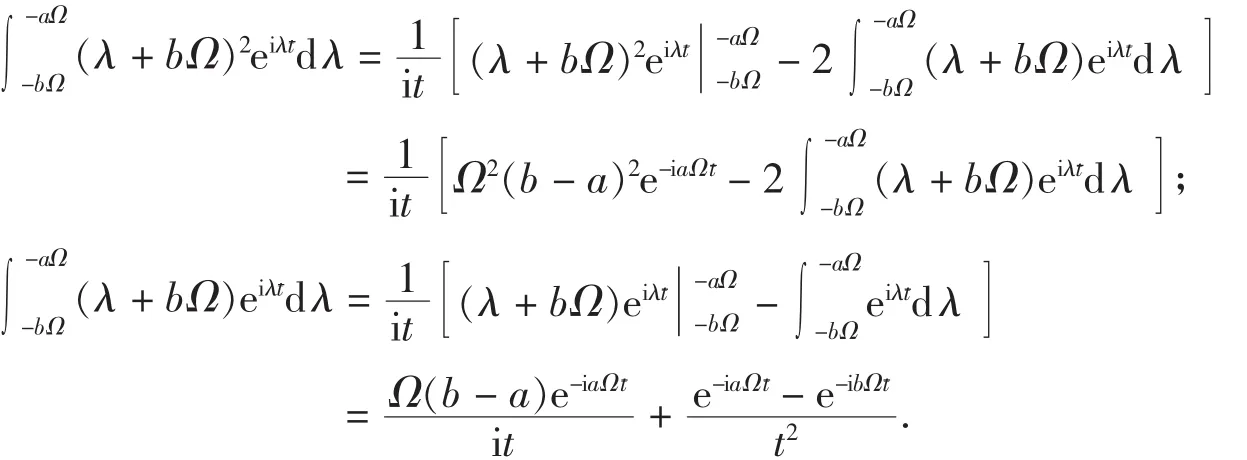
所以有：

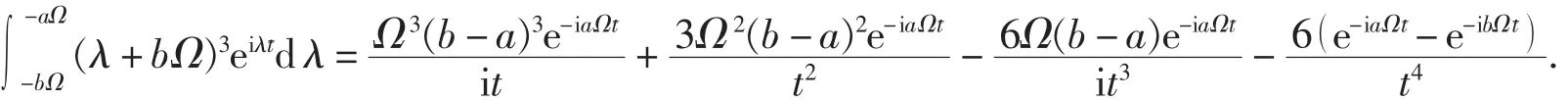
类似地，可以计算：

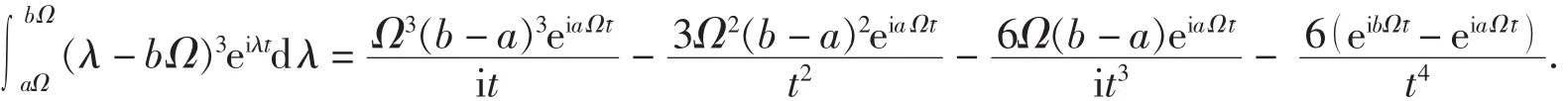
所以，

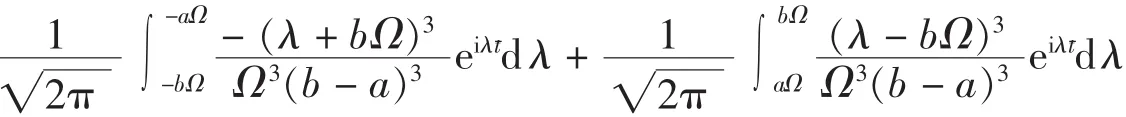
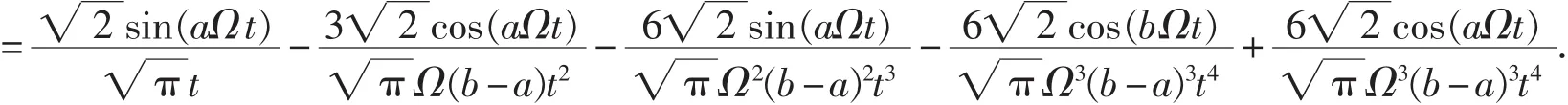
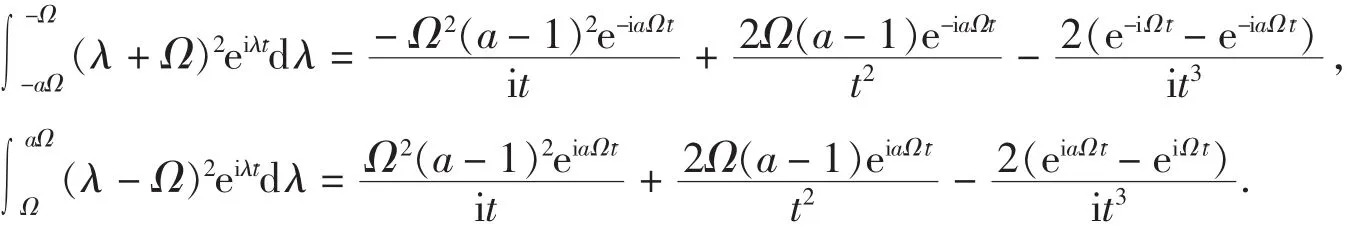
第三步，计算

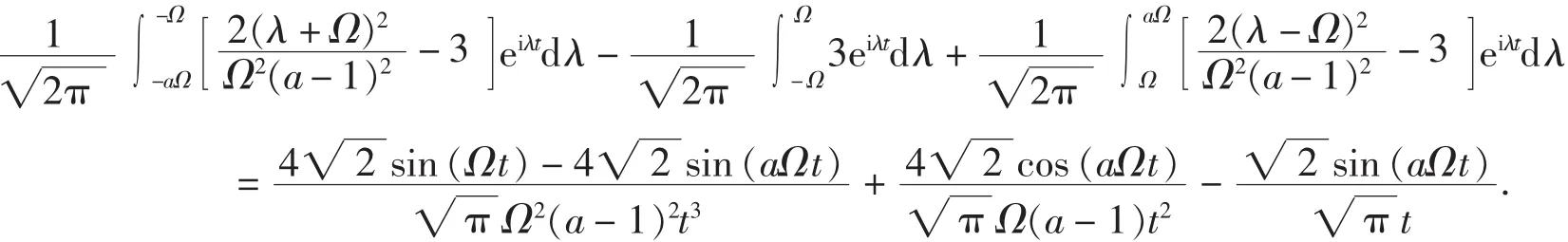
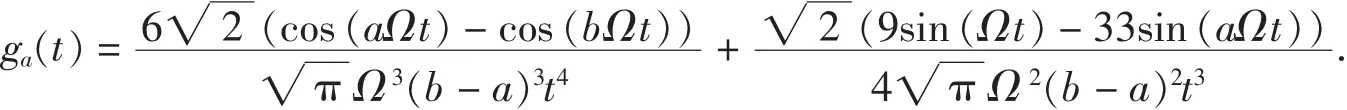
定理2 设ga（t）为定理1中式（2）定义的函数，则对任意分段光滑且连续的带限信号 f（即 Suppf⊆[- Ω，Ω ]）均有：

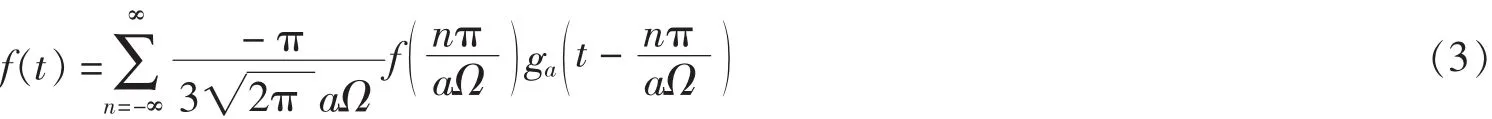
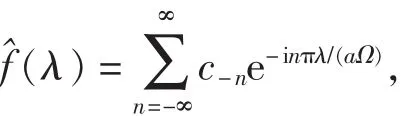
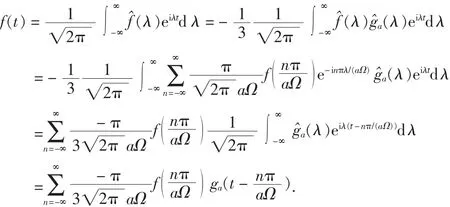
2 结 语

从定理2中的式（3）与引理3的重构结果相比来看, 式（3）提升了重构带限信号f的收敛速度，使其收敛阶由O（n-2）增加到O（n-3），且在b不大于引理3中的h的条件下，并没有增加采样点的个数.

[1]Shannon C E.Communication in the presence of noise[J].Pro IRE， 1949（37）： 10-21.

[2]Walter G G. A sampling theorem for wavelet subspace[J]. IEEE Trans Informat Theory，1992（8）： 881-884.

[3]王旭，邓彩霞，朱建立.再生核Hilbert空间中的采样定理[J].哈尔滨理工大学学报，2008（18）：66-68.

[4]Liu Youming， Walter G G.A class of band-limited cardinal wavelets[J].Adv in Math（China），1997（26）： 523-528.

[5]王里青，徐琼，王凤琼.关于Shannon采样定理的一点注记[J].四川大学学报，2004（41）：1076-1077.

[6]杨守志，程正兴，唐远炎.二维连续信号的近似采样定理[J].应用数学和力学,2003（24）：1097-1203.

[7]杜学明，杨万年.关于小波子空间上的具有紧支撑的采样定理[J].重庆大学学报（自然科学版），2002（25）： 79-82.

[8]Boggess A，Narcowich F J.小波与傅里叶分析基础[M].芮国胜，康健，译.北京：电子工业出版社，2004.

Abstract：Based on the oversampling method， Shannon sampling theorem is improved and a new sampling theorem with high convergence order is obtained.

Key words：Shannon sampling theorem； oversampling； convergence order

Construction of Sampling Theorem with High Convergence Order

XIE Chang-zhen，CHEN Gui-zhang
（Department of Mathematics， Shantou University， Shantou 515063， Guangdong， China）

O 174.2

A

1001-4217（2010）04-0033-05

2010-04-29

谢长珍（1964－），女，河南南阳人，副教授，硕士生导师.研究方向：小波分析.E-mail：czxie@stu.edu.cn

汕头大学科研基金项目（YR09010）