序约束下双参数指数分布的Fiducial参数估计

王 敏，刘全辉，高玉丽

（鲁东大学数学与信息学院，山东 烟台 264025）

序约束下双参数指数分布的Fiducial参数估计

王 敏，刘全辉，高玉丽

（鲁东大学数学与信息学院，山东 烟台 264025）

利用Fiducial统计推断的方法，给出双参数指数分布参数的Fiducial模型，然后基于参数的Fiducial模型给出两总体序约束下参数的Fiducial分布，得到序约束条件下未知参数的Fiducial参数估计的具体解析式，同时给出两总体序约束下未知参数的参数估计的数值解.对于总体个数大于2的情况，根据Fiducial模型给出相应的参数估计的数值计算方法，并进行数值模拟，结果证明由这种数值方法所得到的数值解的误差是可以接受的.

Fiducial模型；Fiducial分布；枢轴模型；序约束

0 引 言

双参数指数分布的应用很广泛，尤其是在可靠性工程中，经常用指数分布来描述车辆、液压设备、泵等的寿命.但由于可靠性统计的对象大都是比较精密、昂贵的设备，能做的试验少，数据得来不易，所以用经典方法对可靠性统计中所需要的指标进行推断不太容易.Bayes方法可以利用经验的知识，减少试验的量.但是如果经验的知识很少，或者几乎不了解，此时可以用Fiducial方法进行处理. Fiducial方法就是在没有任何先验信息的时候，给出在给定样本观测值的条件下参数的条件分布，以替代由Bayes定理得到的后验分布.

参数的Fiducial分布最初是由Fisher于1930年引入的，主要研究单参数、单变量的连续型分布族.此后，一批统计工作者相继在这方面作了许多工作，至今已有几种求Fiducial分布的方法.Fraser[1－2]在变换分布族下给出了Fiducial分布，他所给的Fiducial分布，实际上是在Haar测度为先验下的后验分布.后来，Fraser[3]将他的方法推广到结构模型.在这方面，Hora和Buehler[4－5]也做了一些工作.Dawid和Stone[6]以及Dawid和Wang[7]提出了另外一种求Fiducial分布的方法，他们考虑的模型是函数模型.除了上面两种方法，Barnard[8]从枢轴模型给出了Fiducial推断，他所给的Fiducial分布是从枢轴量的已知分布变换而得.然而，能用已有的方法得到Fiducial分布的情形还是有限的.

2006年，徐兴忠[9]在《中国科学》上正式发表《枢轴分布族中的Fiducial推断》一文，将Dawid和Stone的工作进行推广，给出了Fiducial模型和Fiducial分布的概念，以适应更广泛的分布族.本文拟利用文献［9］中的理论方法，给出双参数指数分布的Fiducial参数估计.对于无约束条件下双参数指数分布的Fiducial推断，文献［10］中已有详细解答，因此，本文主要给出序约束条件下双参数指数分布的Fiducial参数估计.

1 预备知识

文献［9］对Fiducial模型和Fiducial分布的定义是在枢轴分布族中定义的.

定义1[9]设定义在空间χ上的随机变量X的分布属于枢轴分布族{Pθ：θ∈Ω}，χ，Ω都是Borel集，它们可以有不同的维数，是它的一个结构模型，其中，Z为分布完全已知的随机变量，其分布用Q表示， “”表示两边随机变量同分布.是对应的结构方程，其中x，z分别是随机变量X，Z的观测值.在χ上定义距离（·，·），设是使得 d（x，h（θ，z））在 Ω 上达到最小值的 θ值， 即：

定义2[9]设是χ上的枢轴分布族，g（θ）是未知参数θ的一个函数.若是由定义 1 确定的 Fiducial模型，我们称是 g（θ）的 Fiducial模型， 并称 g（（Z））在 Q 下的分布是 g（θ）的 Fiducial分布， 记为 HxG（·）.

在上述定义指导下，可以找到双参数指数分布总体中未知参数的Fiducial分布，从而可对总体进行一系列推断.为此，先作如下假定.

设有k个双参数指数分布总体，第i个总体Xi的概率密度函数为：

记为 Xi～ E（αi，βi）， E 表示指数分布.

（Xi1，Xi2，…，Xini），i=1，2，…，k 分别是来自第 i个双参数指数分布总体的简单随机样本，是第i个总体的样本的最小次序统计量，i为第i个总体的样本均值.

记参数 α ＝ （α1，α2，…，αk）， β ＝ （β1，β2，…，βk）. 一般情况下, 它们满足一定的约束条件，如最简单的序约束：

以下，本文将在这两个约束条件下讨论双参数指数分布中未知参数的估计问题.为此，先计算序约束下参数的Fiducial分布.

2 主要结果

根据文献［9］所介绍的方法，要求参数的Fiducial分布，需要先根据枢轴模型给出参数的Fiducial模型，再求出参数的Fiducial分布.计算结果显示，参数的Fiducial分布计算起来比较麻烦，而且，很多情况下没有显式表达，因此，以下仅给出两个双参数指数分布总体（k=2）序约束（1）下参数α的Fiducial分布.而对两个总体序约束（2）下β的Fiducial参数估计及其他情况下各参数的Fiducial估计，则给出相应的数值计算的方法.

2.1 序约束下位置参数α的Fiducial参数估计

在两总体序约束情况下，如采用式（1）所表示的序约束形式，可采用与文献［10］相同的方法，得出β已知时，α的枢轴模型为：

其中， Z1， Z2独立同分布， Z1～ E（1）， E（1）表示参数为 1 的指数分布.X（1）， Y（1）分别为两个总体的样本的最小次序统计量.

为了得到序约束（1）下未知参数α1，α2的Fiducial分布，首先找到在这个约束条件下α1，α2的 Fiducial模型. 为此， 令：

在这里， 除 α1，α2外， 其它均为已知的值， x（1）， y（1）， z1， z2分别为 X（1）， Y（1）， Z1， Z2的观测值.

要得到约束条件下 α1，α2的 Fiducial模型， 必须找到在这个约束条件下 D（α1，α2）的最小值点.于是这个问题就转化为下面这样一个求非线性规划的问题：

解这个非线性规划问题，可以得到在约束α1<α2下，参数α1，α2的Fiducial模型分别为：

这里，

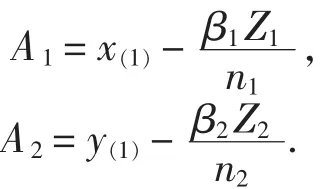
其中Z1，Z2是独立同分布的，Z1～E{1}.

由参数的 Fiducial模型（3）， （4）可以直接找到的联合分布以及它们的边际分布.

1） 当 x（1）≤ y（1）时，的联合分布为：

也可以得到与上面相同的结果.

则可将该期望值作为序约束（1）下未知参数的点估计.其区间估计可由相应的边际Fiducial密度求得.

事实上，也可以由Fiducial模型（3）直接得到它们的数学期望，结果与上面是一样的.

2）当 x（1）>y（1）时， 可以得到的联合分布：

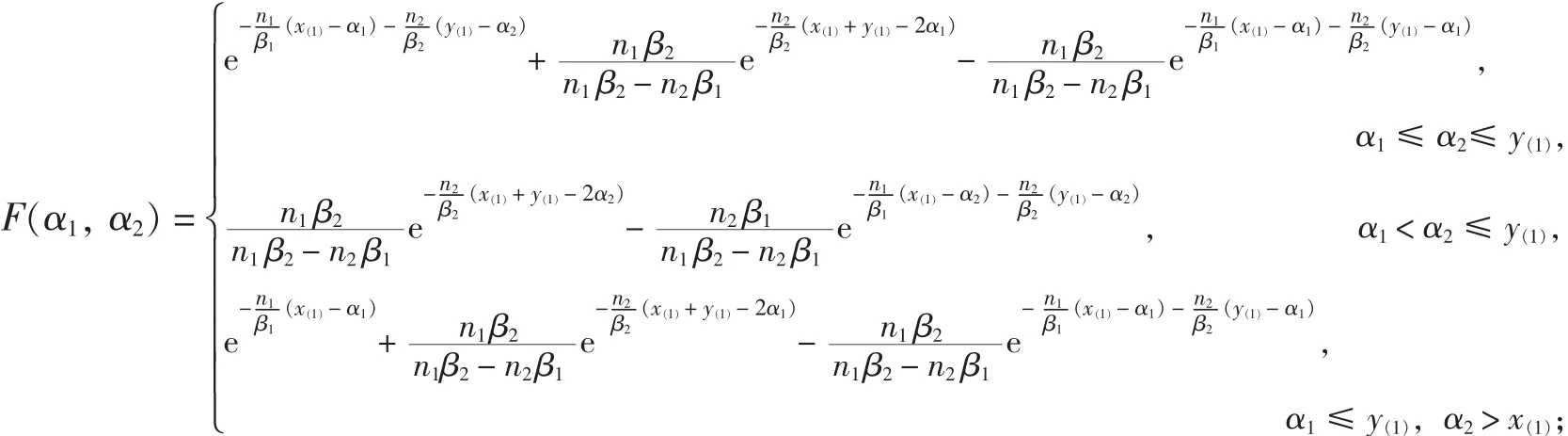
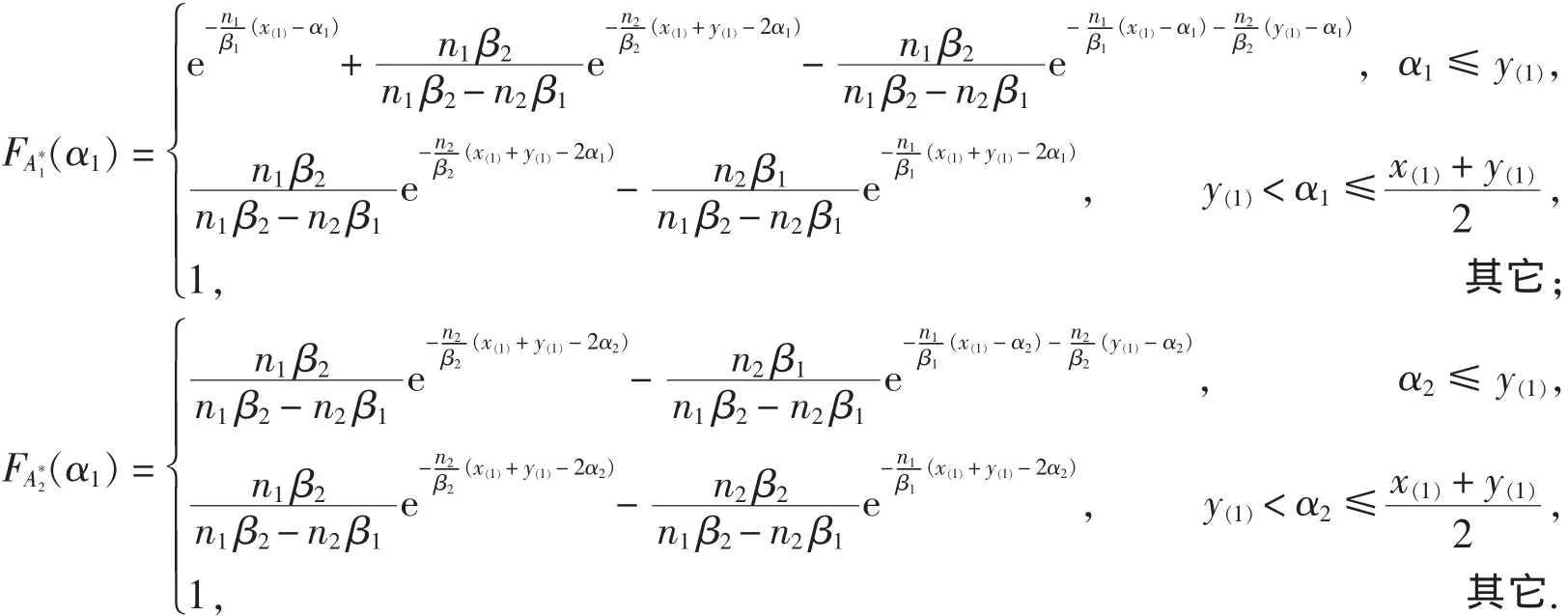
事实上, 由：

可得

同理可得

由此可用两者的均值作为序约束下α1，α2的点估计.

由上面的讨论可以看出，在求参数的期望值，尤其是在带约束的条件下的期望值时，参数的Fiducial分布很难有表达式.当总体个数增加时，寻找显式表达就更加困难，此时可以采用数值计算的方法.

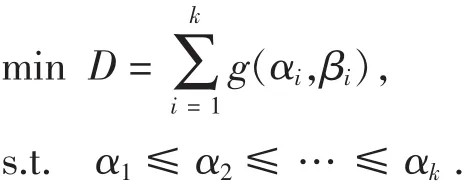
在这个规划问题中，目标函数是k个函数的和，约束条件有个k-1.当k特别大时，寻找最小值点比较困难，这时可以采用数值计算的方法得到在序约束条件下α的Fiducial分布的样本，然后对所得样本观测值求平均值或众数等，来得到α的Fiducial参数估计.具体算法如下.

第一步， 分别找到 g（αi，βi）的最小值点， 记为 αi， i＝ 1，2，…，k. 若满足 α1≤ α2≤…≤αk，则这k个点即为所求的点，否则继续下步；

第二步，找到第一个不满足条件的点，设为αi，即αi满足α1≤α2≤…≤αk，αi＞αi+1；

第三步，令 αi＝ αi+1， 由目标函数 g（αi，βi） +g（αi，βi+1）+g（αi+2，βi+2）得到无约束条件下的最小值点， 仍记为 αi， 令 αi+1＝αi；

第四步，比较αi+1和αi+2的大小关系，若αi+1≤αi+2，则继续两两比较，找到下一个不满足条件的点，按照第三步的方法得到新的最小值点，否则继续下一步；

第五步， 若 αi+1＞ αi+2， 则令 αi＝ αi+1＝ αi+2， 由目标函数为g（αi，βi） +g（αi，βi+1）+g（αi+2，βi+2）， 得到无约束条件下的最小值点， 仍记为 αi， 令 αi+1＝ αi+2＝ αi；

第六步，继续第四、五步的步骤，一直比较到最后一对αk-1＝αk，则得到一列新的值， 仍记为 α1，α2，…，αk，完成一次循环；

第七步，循环进行上述六步，会得到不同的点列，当这列点满足α1≤α2≤…≤αk时, 循环结束，则这列点就是所要求的点.

2.2 序约束下尺度参数β的Fiducial参数估计

两个指数总体下，α已知时，β的枢轴模型为：

其中， Z11， Z12， Z21， Z22相互对立， 且 Z11，Z12～ E（1）， Z21，Z22～ Γ（n-1，1）， Γ（n-1，1）表示参数为n-1，1的伽玛分布.

在序约束（2）下求解β的Fiducial分布较复杂，因此采用与求解α的Fiducial参数估计相同的方法，令：

通过求得该非线性问题的最小值点，进而求得β的Fiducial分布的一组样本点，最终求得β的Fiduical参数估计.这里不作详细说明.

2.3 序约束下（α，β）的Fiducial参数估计

当所有的参数都是未知时，必须从它们的联合枢轴模型得到参数的Fiducial模型.

求解非线性规划问题：设：

但是这个规划问题计算起来比较麻烦，所以一般不直接计算，而是用数值计算的方法得到αi，βi的Fiducial分布的样本点. 具体步骤如下.

第一步， 首先分别找到 f（αi，βi）的最小值点， 记为 ai， bi， 若满足 a1≤ a2≤ … ≤ ak，b1≤ b2≤ … ≤ bk， 则（a1，a2，…，ak）， （b1，b2，…，bk）即为所求点. 否则继续下一步；

第二步，若（a1，a2，…，ak）， （b1，b2，…，bk）中有且只有一组点满足条件，不妨设 a1，a2，…，ak满足条件， 分别将 a1，a2，…，ak代入 f（α1，β1）， f（α2，β2），…， f（αi，βi）， 这样就转化为一个在 α1，α2，…，αk已知的条件下，关于 β1， β2，…， βk的约束问题， 可以按照第 2.1 节的算法来进行.否则继续下一步；

根据上述算法， 取 k=4，α， β的真实值为 α = （0，1，2，3）， β = （1，2，4，6）， 即假定4 个已知总体： E（0，1）， E（1，2）， E（2，4）， E（3，6）， 在这 4 个总体中分别抽取容量为 ni（i=1，2，3，4）的样本， 由这些样本得到总体参数的估计值α， β， 并与其真实值 α， β 进行比较，用Matlab程序，n=（n1，n2，n3，n4）取不同的值，模拟出的结果如表1所示.

表1 α，β的估计值

由上表可以看出，样本容量很大时，用这种算法得到的总体参数的估计值更接近真实值，且不同样本容量得到的估计值之间的误差大部分不超过0.1.因此由这种数值方法所得到的估计值是可以被接受的.

3 结 语

本文利用Fiducial推断的方法，给出了双参数指数分布中未知参数在各种情况下的Fiducial参数估计，从计算过程来看，Fiducial方法相较于经典方法要稍显麻烦，但是Fiducial方法仍是值得采用的一种方法，主要反映在以下几个方面：首先，Fiducial方法主要针对小样本情况下的统计推断，尤其是不需要给出先验分布.其次，虽然很多时候参数的Fiducial分布不容易求，但是利用参数的Fiducial模型可以很方便地给出数值计算的方法，而且所得结果误差在可以接受的范围之内.最后，Fiducial方法对所得结果好坏的评价标准要比经典方法的解释更容易为人们所接受.Fiducial方法对结果的解释是，在对总体进行了一定的观测后，根据所得样本观测值给出了参数的统计推断结果，该结果只与已经出现的结果有关，与没有出现的结果是没有关系的，符合人们的直观想法；而经典统计对结果的解释是，对总体进行充分多次观测后所得结果的平均取值，也就是说，不管某一个样本观测值是否出现，它都要被列入评价范围之内，这对人们来说是难以接受的.

[1]Fraser D A S.On fiducial inference[J].Ann Math Statist， 1961， 32： 661-671.

[2]Fraser D A S.The fiducial method and invariance[J].Biometrika， 1961， 48： 261-280.

[3]Fraser D A S.The structure of inference[M].New York： Wiley， 1968.

[4]Hora R B， Buehler R J.Fiducial theory and invariant estimation[J].Ann Math Statist， 1966， 37：643-656.

[5]Hora R B， Buehler R J.Fiducial theory and invariant prediction[J].Ann Math Statist， 1967， 38：795-801.

[6]Dawid A P， Stone M.The function model basis of Fiducial inference[J].The Annals of Statistics，1982， 10： 1 054-1 067.

[7]Dawid A P， Wang J.Fiducial prediction and semi-Bayesian inference[J].The Annals of Statistics，1993， 21： 1 119-1 138.

[8]Barnard G A.Pivotal models and the Fiducial argument[J].International Statistical Review， 1995，6：309-323.

[9]徐兴忠，李国英.枢轴分布族中的Fiducial推断[J].中国科学A辑，2006（03）：340-360.

[10]Wang Min， Zhang Bao-xue， Xu Xing-zhong.The Fiducial inference on the two-parameter exponential distribution[J].Soochow Journal of Mathematics， 2006， 10（32）： 447-484.

Abstract：The Fiducial model in the two-parameter exponential distribution is given on the basis of the Fiducial estimation method. The Fiducial distribution under the two global order restrictions is presented.The exact expressions to estimate the Fiducial parameters under the order restrictions can be obtained.Since the solutions to the expressions are complex，the parameter estimation solutions under the two global order restrictions are presented.If the global number is over two，the exact expressions cannot be given.The parameter estimation computing method based on the Fiducial model and numerical simulations is proposed.It is shown that the error that is caused by this method can be accepted.

Key words：Fiducial model；Fiducial distribution；pivotal model； order restriction

Fiducial Parameter Estimation on the Two-Parameter Exponential Distribution under the Order Restrictions

WANGMin， LIU Quan-hui， GAO Yu-li
（School of Mathematics and Information， Ludong University， Yantai 264025， Shandong， China）

O 211.3

A

1001-4217（2010）04-0017-09

2010-04-13

王敏（1979－），女，山东烟台人，硕士，讲师.研究方向：Fiducial统计推断.E-mail：wangmin_2001@163.com

鲁东大学校科研基金（042711）