紧支撑正交多小波的构造

李万社，罗立娑，郑李娥

（陕西师范大学数学与信息科学学院，陕西 西安 710062）

紧支撑正交多小波的构造

李万社，罗立娑，郑李娥

（陕西师范大学数学与信息科学学院，陕西 西安 710062）

通过选取初等旋转矩阵和初等反射矩阵，利用多分辨分析以及矩阵理论，给出了一种由已知紧支撑对称正交多小波构造具有相应性质多小波的方法.利用该方法还可以构造出一类平衡小波.最后，结合DGHM紧支撑对称正交多小波给出了具体的算例.

多小波；多滤波器组；对称性；正交性

0 引 言

小波理论发展非常迅速，人们可以根据不同需要构造出不同的小波[1].1988年，Daubechies[2]指出：对于2带小波，除了Haar小波外，不存在任何正交、对称且紧支撑的小波，并且给出了相应的证明.相对单小波而言，多小波能同时具有对称性、正交性、紧支撑性和高阶消失矩等性质，所以，多小波成为小波研究的新热点.1996年，Chui和Lian利用对称性给出了2重多尺度函数和多小波函数，后来又有更多的人对多小波的理论体系作了研究[3-10]，这使多小波在理论应用上趋于成熟.Jiang[4]给出了多带多小波的参数化形式，杨守志等人[5-8]给出了几种多小波的构造方法，Lebrun等人[3，9-10]分别对多小波预滤波和平衡处理作了研究.还有更多的文献对多小波的构造和性质做了深入的研究.本文根据已有文献的研究，在给定一个紧支撑对称正交多小波的基础上，通过选取初等旋转矩阵和初等反射矩阵[11]，与已知的紧支撑对称正交多小波作乘积，构造出相应性质的多小波.最后，本文构造了相应性质的正交多小波.

1 预备知识

上式中r×r矩阵序列{Pk}k∈Z称为两尺度矩阵序列，Φ（x）称为2尺度r重尺度函数.对式

设 Φ ＝ [φ1，…，φr]T， φ1，…，φr∈L2（R）满足如下方程：

定义1 定义子空间序列Vj⊂L2（R）如下：

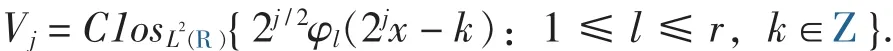
称由式（1）定义的Φ（x）生成一个多分辨分析{Vj}j∈Z，若{Vj}j∈Z满足：构成 Vj的一个 Riesz基.

定义Wj⊕Vj=Vj+1，j∈Z，其中Wj是Vj在Vj+1中的正交补空间.向量函数Ψ（x）=[Ψ1，…，Ψr]T，Ψl∈L2（R），l=1，2，…，r的整数平移构成 Wj的一个 Riesz基，即：

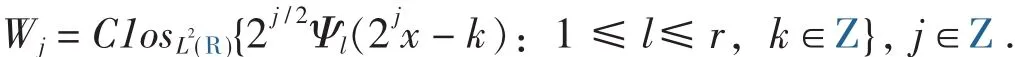
因为 Ψ1，…，Ψr∈W0⊂V1，所以存在 r× r矩阵序列{Qk}k∈Z满足：

定义2[1]若存在正整数k1，k2（k1＜k2）使得当k2＞k且k1＜k时， 有Pk=o，Qk=o，其中 o 是 r× r的零矩阵， 则由式（2）和（4）定义的滤波器组{P（z），Q（z）}称为有限脉冲（FIR）多滤波器组， 同时也称{Φ（x）,Ψ（x）}是紧支撑的.

引理1[1]若U是任意的正交矩阵，Φ（x）和Ψ（x）是多尺度函数和多小波，则仍然是正交的多尺度函数和多小波.

2 紧支撑对称正交多小波的构造

引理2[11]令正交矩阵

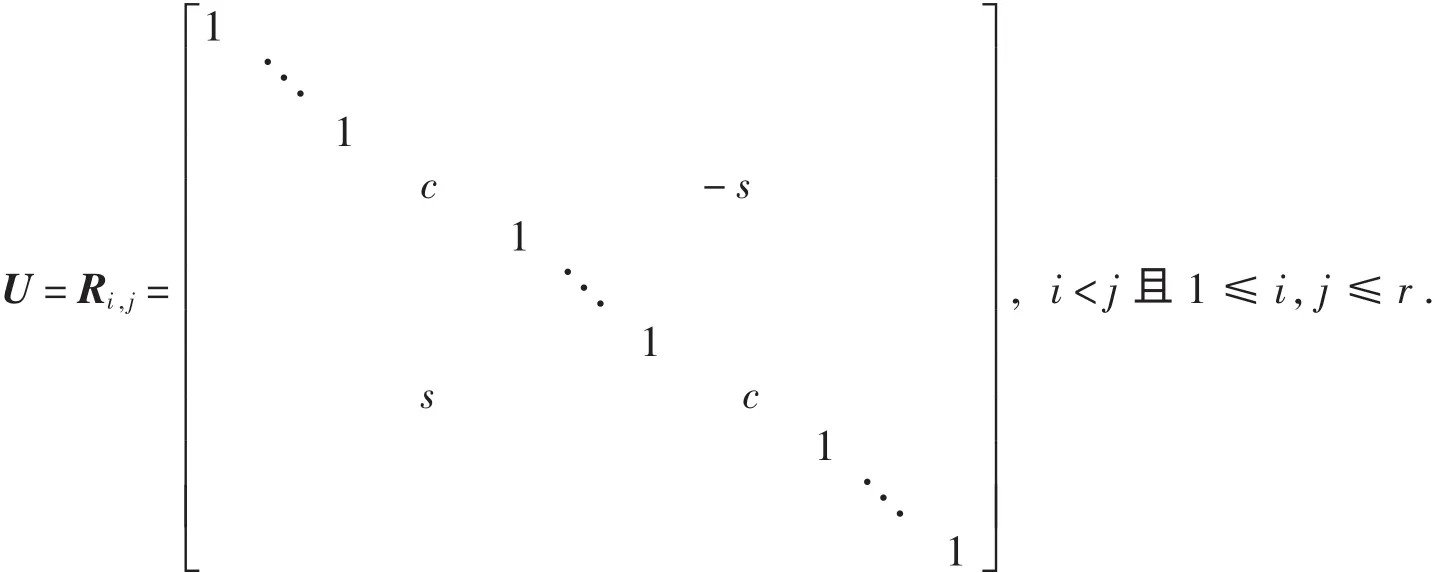
其中c=cos θ，s=sin θ，Ri,j表示除第i列和第j列外其余列都是单位基向量.矩阵中没有写出的元素都是零元素.这样的矩阵称为 Givens 矩阵， 并记 Ri，j=Ri，j（c，s）.

定理 1 若 Φ =[φ1，…，φr]T， Ψ（x）＝ [Ψ1，…，Ψr]T是紧支撑对称正交多小波所对应的多尺度函数和多小波函数， 构造Φ1（x）和Ψ1（x）如下：

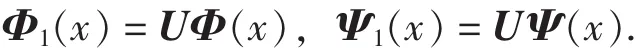
其中， U 是 Givens矩阵， 并且有 Φ1=[φ11，…，φ1r]T， Ψ1（x） ＝ [Ψ11,… ,Ψ1r]T， 则 Φ1（x）和Ψ1（x）分别是紧支撑对称正交多小波的尺度函数和多小波函数.

证明 因为Φ（x）和Ψ（x）是紧支撑对称正交多小波所对应的尺度函数和多小波函数，并且Givens矩阵是正交矩阵，所以由引理1可得，Φ1（x）和Ψ1（x）仍然是紧支撑对称正交多尺度函数和多小波函数.

定理 2 若{P1（z），Q1（z）}是定理 1 中所构造的 r重紧支撑对称正交多小波{Φ1（x），Ψ1（x）}的 FIR 滤波器组， {P（z），Q（z）}是{Φ（x），Ψ（x）}的滤波器组， 则有：

其中，

证明 由 Φ（x） =U-1Φ1（x）可得： Φ（2x-k） =U-1Φ1（ 2x-k ）.由式（1）可得：

所以， P1（z） =UP（z）U-1.同理可得：Q1（z） =UQ（z）U-1.从而有：

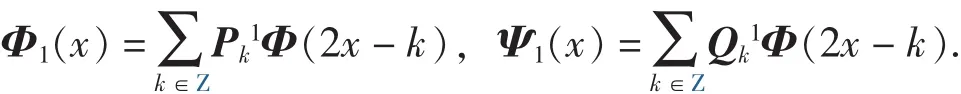
命题得证.

定理3 条件同定理1，设Φ1（x）和Ψ1（x）是定理1中所构造的多尺度函数和多小波函数，则有：

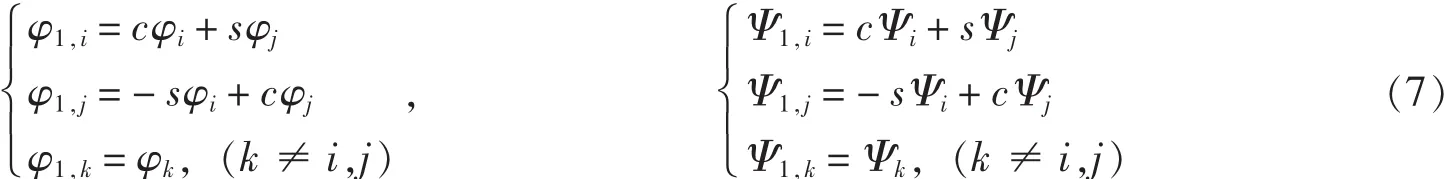
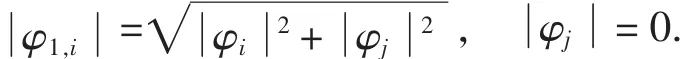
下面借助初等反射矩阵构造多尺度函数和多小波函数.

定义3[11]一般地，在Rn中，可以定义关于 “法线为单位向量u的n-1维子空间”对称的变换.设单位向量u∈Rn，称H=I-2uuT为Householder矩阵（或者初等反射矩阵）.由初等反射矩阵确定的变换称为初等反射变换.

引理3[11]Householder矩阵是对称矩阵，即HT=H；是正交矩阵，即HTH=I；是自逆矩阵，即H-1=H；是对合矩阵，即H2=H；行列式为-1，即det H=-1.

引理4[11]初等旋转矩阵是两个初等反射矩阵的乘积.

定理 4 若 Φ =[φ1，…，φr]T，Ψ（x）＝[Ψ1,… ,Ψr]T是紧支撑对称正交多小波所对应的多尺度函数和多小波函数， 构造 Φ2（x） ,Φ3（x）和 Ψ2（x），Ψ3（x）如下：

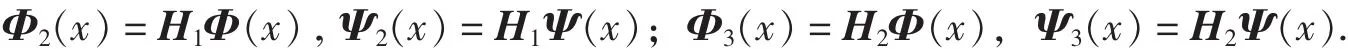
其中Householder矩阵H1,H2如下：

令H1中θ为3θ便得H2=I-2vvT，并且有：

Φ2=[φ21，…，φ2r]T， Ψ2（x） ＝ [Ψ21，…，Ψ2r]T； Φ3=[φ31，…，φ3r]T， Ψ3（x） ＝ [Ψ31，…，Ψ3r]T.则 Φ2（x），Φ3（x）和 Ψ2（x），Ψ3（x）分别是紧支撑对称正交多小波的尺度函数和多小波函数.

定理 5 Φ1（x），Φ2（x），Φ3（x）和 Ψ1（x），Ψ2（x），Ψ3（x）如前面定理所构造， 则：

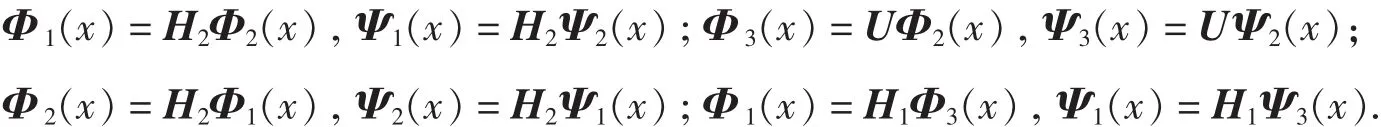
由上面的构造过程可以看出，根据初等旋转矩阵和初等反射矩阵的性质以及引理1，构造出了一系列相关的多尺度函数和多小波函数.

定理 6 Φ1（x） ,Φ2（x） ,Φ3（x）和 Ψ1（x） ,Ψ2（x） ,Ψ3（x）如前面定理所构造， 则：

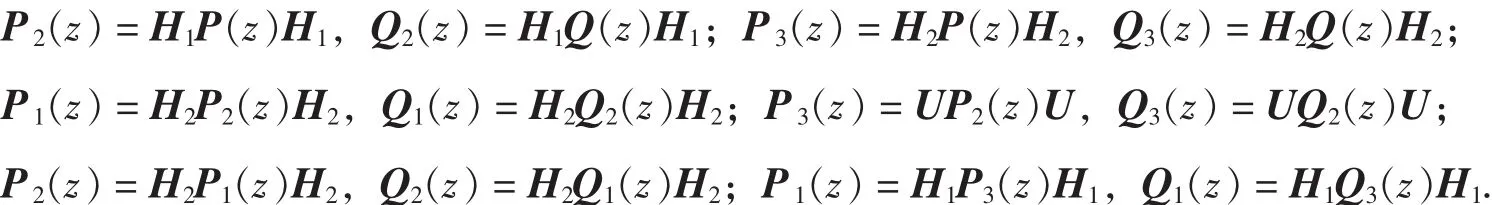
推论 CL2多小波[1]的一阶正交平衡器是定理1中Givens矩阵参数θ＝π/4时的结果.

注[2]在多小波的平衡理论中，这是一个很特殊的平衡器，它对原小波基作了π/4角度的旋转，多数多小波都可以通过它来达到一阶平衡.

3 算 例

已知具有2阶消失矩支集长度是4的对称正交多小波DGHM滤波器系数如下：

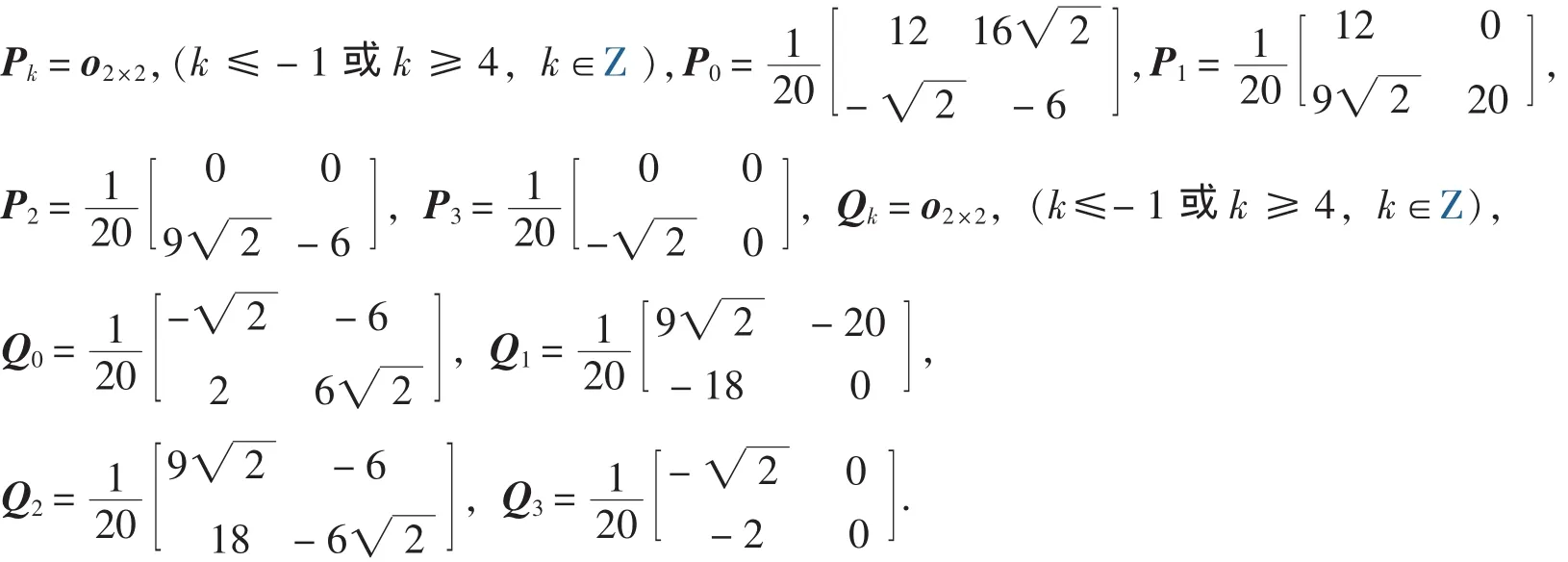
其中多小波基 Φ =[φ1，φ2]T是紧支撑的， 并且 supp φ1=[0，1]， supp φ2=[0，3]， 由式（2）：

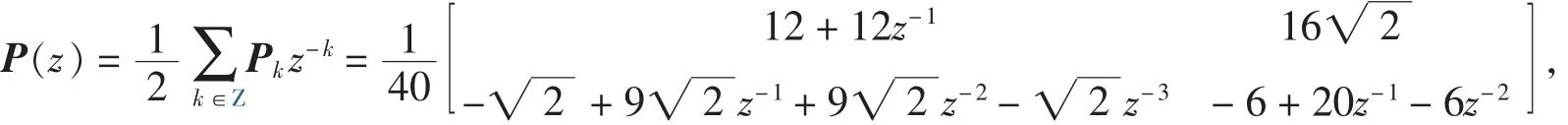
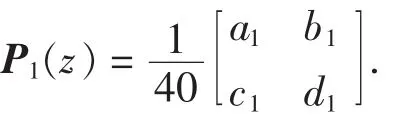
其中，

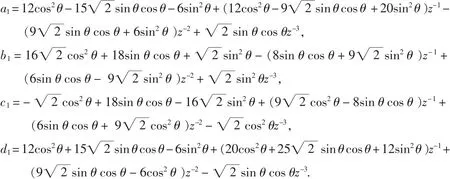
由式（4）可得：

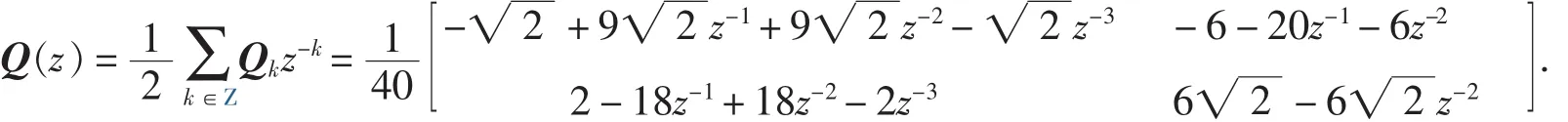
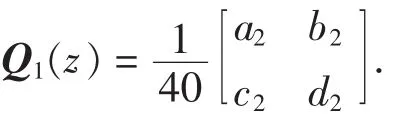
其中，

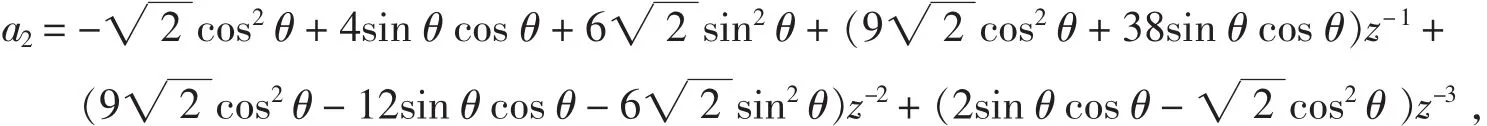
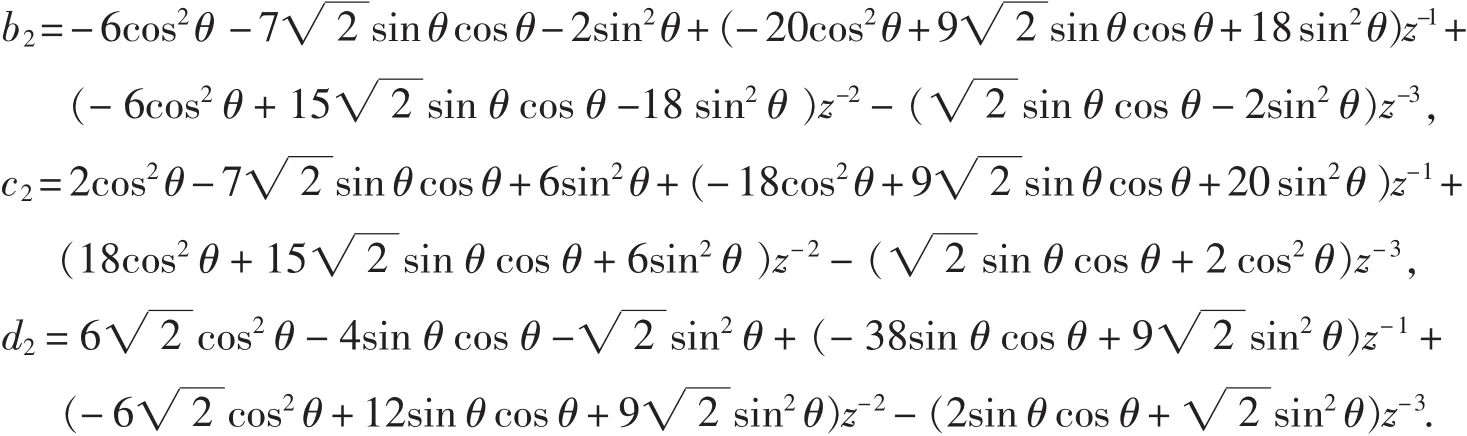
以上所得到的{P1（z），Q1（z） }即为所构造的与{P（z），Q（z）}具有相同性质的多小波的滤波器组，其中参数θ可以根据需要来确定，从而得出不同的结果.特别地，取θ=ω/4就得到了CL2多小波的一阶正交平衡器，使DGHM满足一阶平衡.

[1]唐远炎，王玲.小波分析与文本文字识别[M].北京：科学出版社，2004.

[2]Daubechies I.小波十讲[M].李建平，杨万年，译.北京：国防工业出版社，2004.

[3]Lebrun J， Vetterli M.Balanced multiwavelets theory and design[J].IEEE Trans on Signal Processing，1998， 46（4）： 1 119-1 125.

[4]Jiang Q T.Parameterization of m-channel orthogonal multifilter banks[J].Advances in Computational Mathematics， 2000， 12： 189-211.

[5]杨守志，唐远炎，程正兴.a尺度紧支撑正交多小波的构造[J].计算数学，2002，24（4）：451-461.

[6]崔丽鸿，程正兴.多小波与平衡多小波的理论和设计[J].工程数学学报，2001，18（5）：105-116.

[7]全宏跃，王国秋.一类对称正交多小波的构造[J].应用数学学报，2008，31（4）：682-691.

[8]Chui C K， Lian J A.A study of orthogonal multi-wavelets[J].Appl Numer Math， 1996， 20（3）：273-298.

[9]Lebrun J，Vetterli M.High order balanced multiwavelets[C]. In Proc IEEE int Conf Acoust Speech Signal Proce（ICASSP）， 1998： 12-15.

[10]Lebrun J，Vetterli M.Balanced multiwavelets[C]. In Proc IEEE int Conf Acoust Speech Signal Proce（ICASSP）， 1997， 3： 2 473-2 476.

[11]胡茂林.矩阵计算与应用[M].北京：科学出版社，2008.

Abstract：In this paper,a method is given to generate a new multi-wavelet with the corresponding properties from a compactly supported symmetric orthonormal multi-wavelet by choosing elementary rotation matrix and elementary reflection matrix. A class of balanced wavelets can also be constructed using this method. At last，the DGHMcompactly supported symmetric orthogonal multi-wavelet is given in the method as an example.

Key words：multi-wavelet； multi-filter bank； symmetric； orthonormal

Construction of Compactly Supported Orthonormal Multi-Wavelet

LI Wan-she， LUO Li-suo， ZHENG Li-e
（College of Mathematics and Information Science， Shaanxi Normal University， Xi’an 710062， Shaanxi， China）

O 174.2

A

1001-4217（2010）04-0026-07

2010-06-02

李万社（1963-），男，陕西西安人，教授.研究方向：智能信号处理.E-mail：liwsh@snnu.edu.cn

国家自然科学基金资助项目（10571113）.