几种特殊矩阵的Pareto特征值问题

齐亚超, 陈雄达（同济大学数学系，上海 200092）

几种特殊矩阵的Pareto特征值问题

齐亚超, 陈雄达
（同济大学数学系，上海 200092）

Pareto特征值问题是定义在正卦限上一类锥约束问题，在许多领域有着深厚的背景。将讨论Pareto特征值的一些理论性质，包括给定矩阵Pareto特征值范围及个数上界。引进了一类新矩阵，讨论并给出它的部分理论性质，可直接计算其最大Pareto特征值。

Pareto特征值；锥约束；特征值；非负矩阵；加边矩阵；对偶锥

0 引言

虽然Pareto特征值问题的提法简单，却具有全新的理论研究价值和广阔的实际应用性，是传统的代数特征值问题的推广和扩展，开拓了新的数学理论领域。在Seeger已经做出的一些重要理论的基础上[1]，我

们对Pareto特征值做了进一步讨论。首先我们规定一些使用符号：欧氏空间ℝ的内积x,y=，相应的欧氏范数，欧氏空间正交x⊥y 表示x,y=0。同时，记N={1,2,…,n}，指标集I,J⊆N，我们采用如下记号：

则称C 为一个凸集。一个锥若是凸集，称为凸锥。如果凸锥K 又是一个闭的，那么称K是一个闭凸锥。我

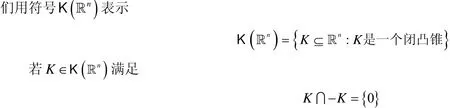
则称锥K 是有指向的。换言之，一个凸锥K是有指向当且仅当它不包含任何直线。

定义0.2 假设锥K∈K(ℝn)，称集合

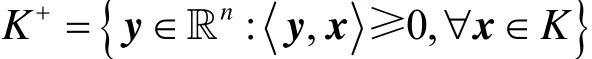
为锥K 的对偶锥。从集合意义上说，若内积为欧氏内积，则锥K∈K(ℝn)的对偶锥就是与K中任意向量夹角为锐角的向量组成的锥。

问题1 给定实矩阵A∈M及锥K∈K(ℝn)，我们称如下问题为锥约束特征值问题，具体形式为

n

求解λ∈ℝ和非零向量x∈ℝn满足

其中K+表示锥K∈K(ℝn)的对偶锥。特别地，下面两种情况：

当K=ℝn时，K+退化为零点，即K+={0}，(0.2)为如下形式

求解λ∈ℝ和非零向量x∈ℝn满足

此时锥约束特征值问题称为Pareto特征值问题。如果存在非零向量x∈ℝn满足(0.4)，则我们称实数λ是给定实矩阵A∈Mn的一个Pareto特征值。相应地，x 称作实矩阵A对应Pareto特征值λ的Pareto特征向量。实矩阵A∈Mn的Pareto特征值集合称作A 的Pareto谱，记做σpareto(A )={λ∈ℝ:(x ,λ)是问题(0.4)的解}。

n

公式(0.4)也可以写作如下形式：

+条件。

问题2 给定实对称矩阵A∈Mn，求解如下形式约束最优化问题：

由以上可知，普通的约束优化问题可以转化为Pareto特征值问题求解。

本文对如下问题进行研究：一是Pareto特征值的理论，包括给定实矩阵Pareto特征值界问题和n维实矩阵Pareto特征值个数上界；二是对正矩阵Pareto特征值进行讨论，确定其最大最小Pareto特征值；三是引进一类新矩阵Q-矩阵，讨论它的部分理论性质，且它的最大Pareto特征值可被直接计算。

1 预备知识

为方便读者，在此我们把一些Pareto特征值相关知识做简单介绍(参见文献[2～6])。我们对指标集I⊆N，记I为集合I的势，即I中元素个数。

若集合S⊆ℝn，存在r＞0，使得B(x,r)=⊆S ，则称x∈ℝn是S的内点，S的所有内点的集合成为S的内部，记做int(S)。

若集合S⊆ℝn，如果S∩B(x,r)≠∅,∀r＞0，则x称为属于S 的闭包，记做x∈S ；如果S=S, 则S称为闭集。

对于如何求解Pareto特征值问题，有如下定理：

定理1.1 (参见[2]) 假设A∈Mn，则λ∈ℝ的一个Pareto特征值当且仅当存在非空指标集I⊆N={1,2,…,n}和一个向量满足是实矩阵A相应于Pareto特征值λ的一个Pareto特征向量。

计算一个给定实矩阵A的Pareto特征值谱比求解其普通特征值谱更困难。我们可以看到(1.2)是求解其

的离散Fenchel共轭，ℕ表示自然数集。

2 正矩阵Pareto特征值

则称A 为正矩阵，记做A＞0。

同时，记

注 在与Pn有关的矩阵性质中，我们可以放松Pn的矩阵类，由正矩阵放松为不可约非负矩阵。

对于正矩阵A∈Pn，有如下Perron定理：

定理 2.1 (Perron定理)[8]如果A∈Mn，且A＞0，则

ρ(A)＞0；

ρ(A)是A的一个特征值；

存在x∈ℝn且x＞0，Ax=ρ(A)x；

ρ(A)是矩阵A的代数重数(和几何重数)为1的特征值；

对λ≠ρ(A)，有|λ|＜ρ(A)，即ρ(A)是唯一的绝对值最大的特征值。

其中λ是正矩阵A 的普通特征值。 Perron定理指出：对于正矩阵A∈Pn有唯一的一个绝对值最大的单重正特征值ρ(A)，且相应的特征向量x可以取为分量全部大于0的正向量，即 x＞0，Ax=ρ(A)x，我们称ρ(A)为正矩阵A 的Perron特征值，并记做ρperron(A)。 由(0.4)可知，ρperron(A)也是矩阵A的一个Pareto特征值，x＞0是相应的Pareto特征向量。接下来，我们讨论给定正矩阵A∈Pn的Pareto特征值，记

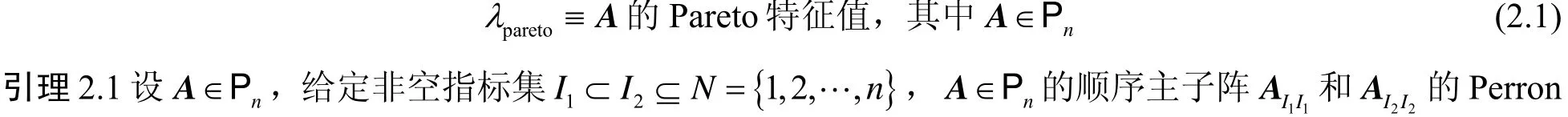
3 实矩阵Pareto特征值界问题

对一般实矩阵A∈Mn的Pareto特征值界，有如下性质：

4 Q-矩阵Pareto特征值

在前面章节，我们讨论了A∈Mn的最小Pareto特征值和最大Pareto特征值ρperron(A)以及一般矩阵的Pareto特征值界。同时，我们也对如下加边矩阵的最大Pareto特征值感兴趣。

定义 4.1 假定A,B,C,D是正矩阵，相应的维数是n×n，m×n，n×m，m×m，我们称正矩阵A的加边矩阵

为列向量符号相同矩阵。因为任意i∈N={1,2,…,n}，列向量Q(:,i)＞0以及i∈M={n+1,n+2,…,n+m}。

特别地，常数0α＞时，我们记列向量符号相同矩阵为

我们采用记号

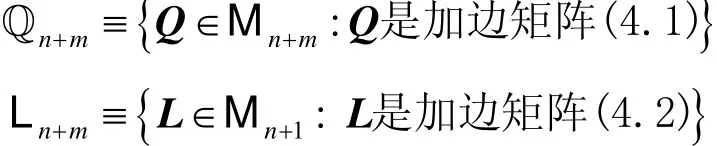
首先来看一个引理。

相应的Pareto特征向量可取为

证明 根据主子阵的选取，非空指标集I可以分为三类：

主子阵普通特征值为-α, 相应的全部正普通特征向量为0＜x∈ℝ，又因为v＞0, 所以

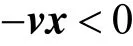
即满足定理2.2中条件(2.2)的子阵普通特征值和普通特征向量均不满足中条件(2.3)。因此，此时不存在矩阵L的Pareto特征值；

其他情形

将其改写为分块形式

相应的Pareto特征向量可取为

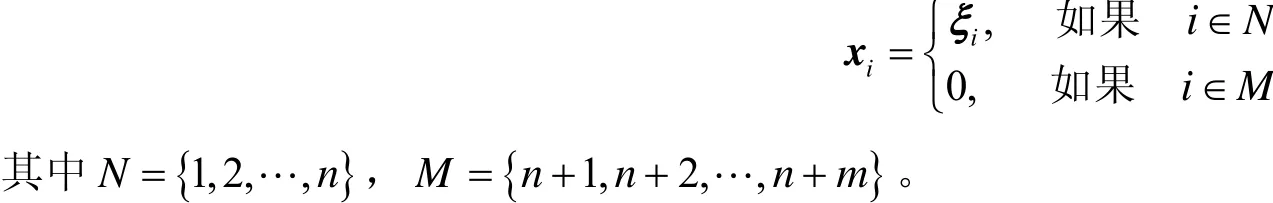
证明 根据主子阵的选取，非空指标集I可以分为三类：

即满足定理2.2中条件(2.2)的子阵普通特征值和普通特征向量均不满足中条件(2.3)，因此，此时不存在矩阵Q的Pareto特征值；

其他情形

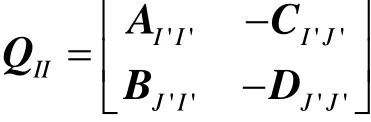
其中I'⊆N，J'⊆M。由定理4.2知，所有主子阵的λpareto,max(AII)都小于其所包含正矩阵AI'I'的最大普通特征值ρperron(AI'I')，再由单调性(2.4)知，

5 Pareto特征值个数上界问题及数值结果

表1给出Mn(n∈{2,3,4,5})Pareto特征值个数上界(参见[2])，特别地，我们找到4×4和5×5分别有23和57个Pareto特征值的实矩阵，数值结果在表2中给出。这些矩阵全部都是Q-矩阵，Q-矩阵比其他类型矩阵可以具有更多的Pareto特征值。Pareto特征值个数比表2中πn更大的矩阵似乎是存在的，但目前为止，在数值计算中还没有更好的结果。

表1 空间Mn(n∈{2,3,4,5})的Pareto特征值个数上界Tab.1 Bounds (1.6) for the Pareto capacity of spaces Mnforn∈{2,3,4,5}

6 结论及开放问题

本文中，我们研究了Pareto特征值的理论，包括给定正矩阵的最大Pareto特征值和实矩阵Pareto特征值界问题。特别地，我们引进了一类新矩阵Q-矩阵，给出它的部分理论性质，它的最大Pareto特征值可被直接计算。

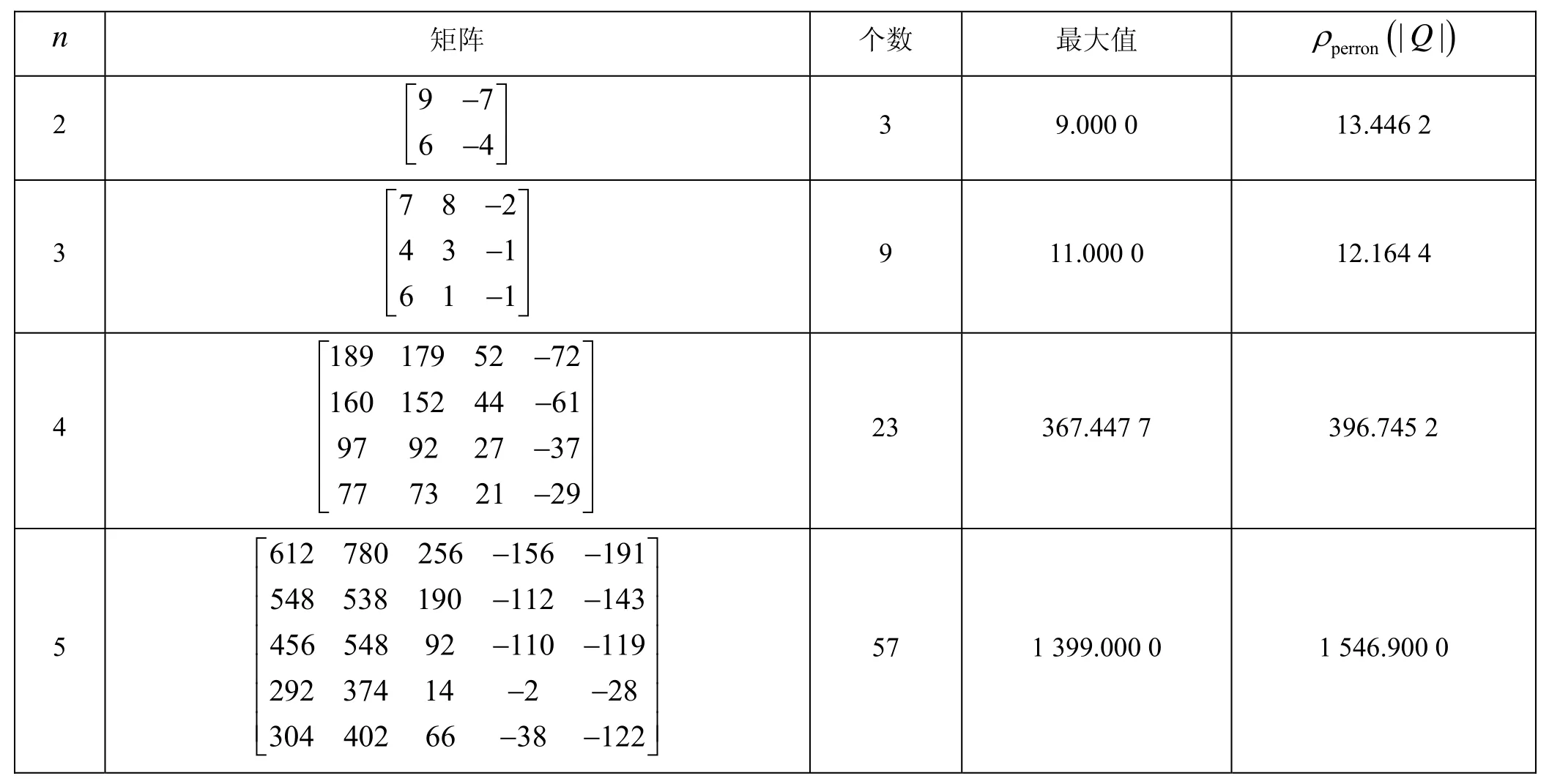
表2 矩阵Q的Pareto特征值Tab.2 The Pareto eigenvalue associated with Q-Matrix

对正矩阵A∈Pn，有

其中A是矩阵L或Q中所含最大正顺序子矩阵。

对n=4,5，Mn空间Pareto特征值个数界πn满足

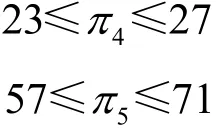
最后，我们提出一些开放问题讨论：

得到πn的精确值相当困难。到目前为止，我们知道9≤π3≤10，23≤π4≤27和57≤π5≤71。 但不幸的是，我们并不知道π3，π4和π5的精确值，是否有方法可以改进一个给定的n×n实矩阵，使其有更多的Pareto特征值？

我们发现一个有趣的现象，如果Q-矩阵A的平方矩阵依然是一个Q-矩阵，则平方矩阵A2经常比A 有更多的Pareto特征值，平方矩阵A2的性质如何？其是否能够帮助我们得到π的精确值？

n

[1] IUSEM A, SEEGER A. On convex cones with infinitely many critical angles[J].Optimization, 2007, 56: 115－128.

[2] PINTO D COSTA A, SEEGER A. Cone-constrained eigenvalue problems: theory and algorithms[J]. Computational Optimization and Applications, 2008, 45: 25-57.

[3] SEEGER A. Eigenvalue analysis of equilibrium processes defined by linear complementarity conditions[J]. Linear Algebra and Its Applications,1999, 292: 1－14.

[4] SEEGER A, TORKI M. On eigenvalues induced by a cone constraint [J].Linear Algebra and Its Applications, 2003, 372: 181－206.

[5] SEEGER A, TORKI M. Local minima of quadratic forms on convex cones [J].Journal of Global Optimization, 2009, 44: 1－28.

[6] TAM B. The Perron generalized eigenspace and the spectral cone of a cone-preserving map[J]. Linear Algebra and Its Applications, 2004, 393: 375－429.

[7] LAVILLEDIEU P, SEEGER A. Existence de valeurs propres pour les systèmes multivoques: résultats anciens et nouveaux[J]. Annales des Sciences Mathématiques du Québec, 2000, 25: 47－70.

[8] HORN R A, JOHNSON C R. Matrix Analysis[M].Cambridge: Cambridge University Press, 1985.

[9] ADLY S, SEEGER A. A nonsmooth algorithm for cone-constrained eigenvalue problems, Computational Optimization and Applications[J/OL]. http://www.springerlink.com/content/nw01m1h01gv167v8/, 2009-11-24/2009-11/25.

The Pareto Eigenvalue Problem of Some Matrices

QI Ya-chao, CHEN Xiong-da
(Department of Mathematics, Tongji University, Shanghai 200092, P.R. China)

The Pareto eigenvalue problem(PEP) is an important prototype of cone-constrained problems, which exhibits already many of mathematical difficulties arising in the context of complementarity conditions involving the positive orthant. In this paper, we discuss some theoretical issues such as, the bound of Pareto eigenvalues for given matrices. A new kind of matrix is introduced and analyzed, namely, Q-matrix, whose largest Pareto eigenvalue can be estimated.

Pareto, cone-constrained, eigenvalue, nonnegative matrix, bordered matrix, complementarity

O 212

A

1001-4543(2010)01-0054-011

2009-12-24;

2010-03-01

齐亚超(1984－), 男, 河北人，硕士研究生，主要研究方向为非线性最优化理论，电子邮件：qiyachao@gmail.com,陈雄达(1972－)，男，福建人，副教授，博士，主要研究方向为非线性最优化理论，电子邮件： chenxiongda@yahoo.com。

国家自然科学基金(No.10671145)