一类加工时间依赖资源的链约束排序问题

王洪武，贺小莉(天津科技大学理学院，天津 300457；天津科技大学经济管理学院，天津 300)

一类加工时间依赖资源的链约束排序问题

王洪武1，贺小莉2
(1天津科技大学理学院，天津 300457；2天津科技大学经济管理学院，天津 300222)

考虑了一类工件的加工时间依赖资源，工件具有链约束，目标函数为极小化加权完工时间和的单机排序问题，给出了一个有效的下降算法。

资源约束；排序问题；加权完工时间和；算法。

0 引言

在实际排序问题中，除了处理机外，还需要另外的附加资源。我们把这类排序问题称为具有资源约束的排序问题。一般的有资源约束的排序问题是NP困难的。不可再生资源，工件的加工时间受资源约束，目标函数为最大完工时间的一些排序问题已有多项式时间算法。Blazewicz等在文献[1]中给出了问题的复杂性为O(n2) 的多项式时间算法，文献[2]中给出了复杂性为 O(nlogn)的多项式时间算法。对于目标函数为最小化加权完工时间和的问题，目前其复杂性还未解决。文献 [3]中对提到了一个非常有效的下降算法。本文将该算法推广到工件具有链约束的情况，对链不可中断和链可中断两种情况分别给出了近似算法。

1 模型描述

对于单台机器的排序问题，工件Jj的加工时间为Pj=bj-ajuj，(1≤j≤n)，满足uj≤uj≤，≤U，其中uj是待确定的对工件Jj的资源分配量，aj＞0，bj＞0，为已知常数，∈[0,bj/aj]，为资源分配量的下限和上限，是资源总量。用三阶段法可将我们研究的问题记为

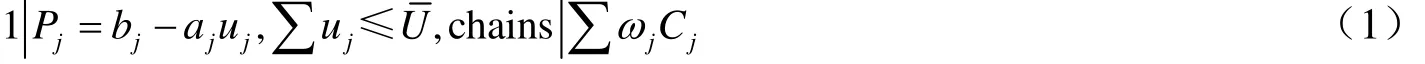
定义1 对于给定的工件集J={J1,J2,…,，用z=(z1,z2,…,zn)表示确定工件可行排序的工件下标对应的一个排列，Z是所有可行排序的集合。满足资源约束的分配向量记为u=(u1,u2,…,un)，所有的可行资源分配向量的集合记为U，使目标函数达到最小的()称为最优解，z*称为最优排序，u*称为最优资源分配。

2 算法及复杂性

对于任意确定的一个满足资源约束的下标排列z∈Z，文献[4]中给出了相应于这一下标排列的最优资源分配的算法1，其复杂性为O(nlogn)。

算法1

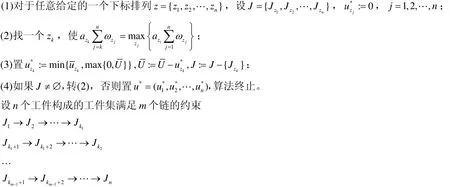
算法1是对给定的下标排列z求一个最优的资源分配。由于集合Z在链不可中断的情况下基数为m!，在链可中断的情况下基数将更大，因此怎样能尽快地求出最优的下标排列z*，是这类问题的困难所在。以下我们将分别对链不可中断和链可中断两种情况构造一个十分有效的下降算法。

2.1 链不可中断的情况

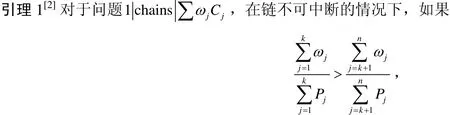
则由工件J1,J2,…,Jk组成的链在由工件Jk+1,Jk+2,…,Jn组成的链之前加工。

定义2 对任一可行排列z∈Z，u*是对应于可行排序z 的最优资源分配，对z 中的第i条链z(i)，记

(1)取初始排序z0∈Z，置k=0；

(2)调用算法1，求相应于zk的最优资源分配uk；

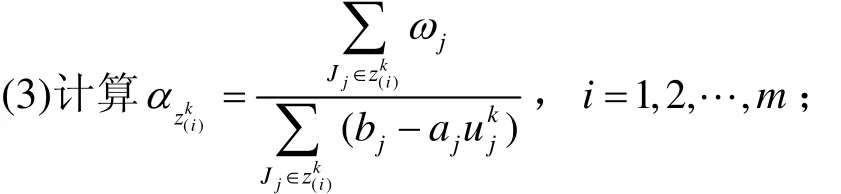
定理2 算法2的目标函数是下降的，算法最终得到的排序是稳定的。

根据推论2.1我们可以对算法2作如下的改进，对链i定义

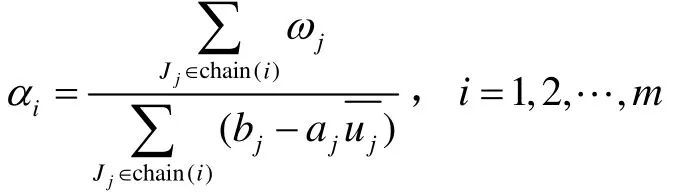
算法3

(1)将所有的链按α非增的顺序排列，得到z0作为初始排序，置k=0；

i

(2)调用算法1，求相应于zk的最优资源分配uk；

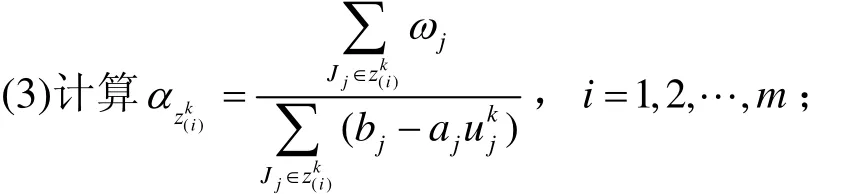
(4)按α的非增顺序重新排列得到zk+1，（若α=α，链i和j 的相对位置不变），如果zk+1=zk，算

z(ki)z(ki)z(kj )法终止；否则k:=k+1，转(2)。

定理3 算法3的复杂性为O(m!mnlog(m+n))。

证明 算法3第一步的复杂性为O(mlogm), 第二步的复杂性为O(nlogn), 即每迭代一次的复杂性为O(mnlog(m+n)), 最多迭代m!次, 所以算法3的复杂性为O(m!mnlog(m+n))。证明完毕。

2.2 链可中断的情况

类似于链不可中断的情况，给出算法5，其复杂性为O(n!mnlog(m+n))。

我们将文献[2]中给出了ρ因子概念推广到工件的加工时间受资源约束的情况。

则上式左端的值称为链J1→J2→…→Jk的ρ因子，记为ρ(1,2,…,k )，Jl*称为决定该链ρ因子的工件。

引理2[2]对确定的资源分配u，如果Jl*是决定链J1→J2→…→Jk的ρ因子的工件，则存在一个最优的排序，在该排序中工件J1,J2,…,Jl*连续加工而不被其它链的工件打断。

对于工件的加工时间确定、链可中断的排序问题(1)，文献[5]给出了一个最优算法。

算法4[5]

(1)在当前未加工的链中选择ρ因子最大的那个链加工；

(2)连续加工已选定的链，直到加工完决定该链ρ因子的工件；

(3)若已加工完全部工件，则停止；否则，转(1)。

下面给出求解工件加工时间受资源约束时的算法。

算法5

(2)调用算法1确定排序zk的最优资源分配u，更新P，j=1,2,…,n；

(3)调用算法4确定所有链的最优排序zk；

(4)如果zk+1=zk算法终止；否则k:=k+1，令所有的工件为未加工的，转(2)。

定理4 由算法5得到的排序zk(k=1,2,…)的目标函数是逐步下降的，算法5的复杂性为

3 进一步的工作

数值例子的计算表明算法3和5是非常有效的。对大部分实例，算法3和5得到的稳定排序就是最优排序。然而，文献[2]中提到对于无链约束的情况，已找到反例，并得到了稳定排序并不是最优排序的充分条件。因为该反例也可以作为本文所研究问题的一个反例，所以排序是稳定的和最优排序之间的关系这一问题还有待进一步的研究。

[1] BLAZEWICZ J, LENSTRA J K, RINNOY KAN A H G. Scheduling subject to resource constraints: classification and complexity[J]. Discrete Applied Mathematics, 1983,5: 11－24.

[2] 唐恒永, 赵传立. 排序引论[M]. 北京: 科学出版社, 2002.

[3] 唐国春, 张峰, 罗守成, 等.现代排序论[M]. 上海: 上海科学技术出版社,2003.

[4] JANIAK A. Time-optimal control in a single machine problem resource constrains[J]. Automatica,1986, 22:745－747.

[5] MICHAEL P. Scheduling: theory, algorithms, and systems[M]. New Jersey: Prentice hall, Englewood cliffs, 1995.

A Kind of Resource-constrained Scheduling Problem with Chains Precedence Constraints

WANG Hong-wu1，HE Xiao-li2
(1 College of Science, Tianjin University of Science & Technology Tianjin 300457, P. R. China 2 College of Economics and Management, Tianjin University of Science & Technology Tianjin 300222, P. R. China)

A kind of resource-constrained scheduling problem in which the processing time has relation to the resources and the job has chains precedence constraints is proposed. The objective is to minimize the total weighted completion time. An effective algorithm is given.

resource-constrained；scheduling problem；the total weighted completion time; algorithm

O223

A

1001-4543(2010)01-0067-04

2009-08-11;

2010-01-14

王洪武（1980－），男，山东寿光人，讲师，硕士，主要研究方向为组合最优化，电子邮件：wanghw@tust.edu.cn。

天津科技大学科学研究基金（项目编号：No.20090217）