西安浅埋暗挖隧道地铁施工的地表沉降分析

李 辉，刘宏飞，宋战平

(西安建筑科技大学 土木工程学院，西安 710055)

西安浅埋暗挖隧道地铁施工的地表沉降分析

李 辉，刘宏飞，宋战平

(西安建筑科技大学 土木工程学院，西安 710055)

以西安地铁长延堡站配线暗挖段为依托，对地表沉降实测数据进行统计分析。结果表明，浅埋暗挖隧道台阶法施工时上(下)导对一定断面沉降的纵向影响范围分别为其前后的2D(2D)和1D(3D)(D为隧道跨度)，且下导开挖所引起的总沉降量大于上导所引起的，其比值约为3/1;横向影响范围约为10D，横向沉降槽曲线符合Peck公式，且给出了沉降槽宽度参数建议值k=0.66。

隧道工程 台阶法施工 地表沉降 横向沉降槽

地表沉降一直是城市地铁隧道开挖过程中较为关注的问题。隧道开挖引发周围土体扰动和破坏，会使地层产生不同程度的地层变形。浅埋隧道由于距离地表较近，地层变形会波及到地表，其变形量的大小和范围直接影响到地上密集城市建(构)筑物、市政工程和道路路面的安全使用。对这个问题国内外的大量学者都进行过相关研究。Rathe Peck早在1969年就提出了经典的沉降槽曲线公式[1]，国内关宝树等[2]也对浅埋暗挖隧道开挖过程中纵向沉降的规律进行了研究。近年来随着电算方法的迅速发展，人工智能预测[3]、数值模拟[4]等已在这个领域开始了广泛的应用。随着地铁建设热潮的到来，如在深圳、北京等地的地铁建设过程中，工程人员和学者们都针对当地的地质对地表沉降进行了广泛的分析和研究，为后来的施工提供了宝贵的经验[5-8]。但由于各地土质的具体性和复杂性，各地的沉降规律都有所不同，对后期施工的预测也只能适用于相似的土质类型。西安作为黄土地区首次修建地铁的城市，通过对隧道开挖过程中所引起的地表沉降规律的研究来预测沉降量和指导施工工艺有非常重要的意义。

1 工程概况

西安市城市快速轨道交通二号线一期工程尤家庄——长延堡段TJSG—18标段会展中心站配线暗挖段区间隧道，位于长延堡站和后配线明挖段之间，走向为南北走向。其北侧为西安市南北交通的主干道之一长安南路，西侧有陕西电视塔、陕西自然博物馆的自然馆和科技馆构成的标志建筑物群。

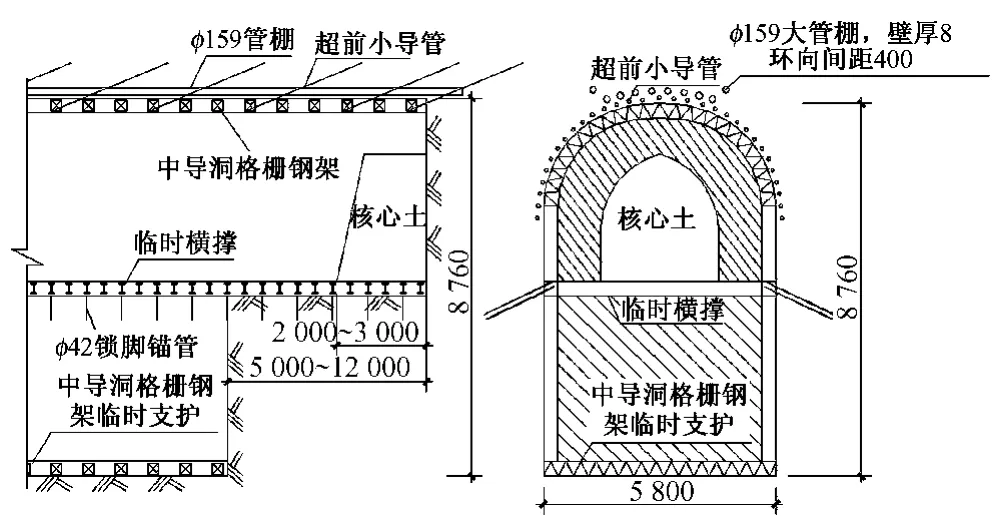
图1 中洞断面及台阶法施工开挖示意(单位:mm)

会展中心站配线暗挖隧道为双联拱断面。联拱隧道采用中导洞超前贯通，中隔墙浇筑及上部回填后用中隔壁(CRD)法开挖两侧洞室。中洞全线长97.1 m，里程为DK20+390.085～DK20+487.185。隧道埋深为11～18 m，开挖宽度5.80 m，高度8.76 m。断面形式为直墙拱形(见图1)。中洞采用短台阶人工小步距开挖，循环进尺1.0 m，风镐配合施工。施工时遵循“管超前、严注浆、短开挖、强支护、快封闭、勤量测”的基本工艺。施工组织计划和施工工序，严格遵守“先排管，后注浆，再开挖，注浆一段，开挖一段，支护一段，封闭一段”的原则进行。

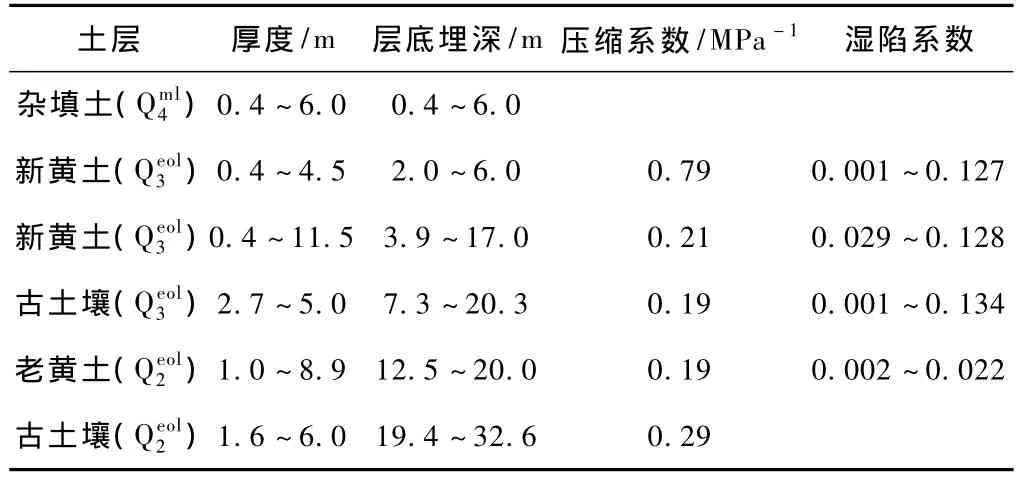
表1 隧道开挖影响土层分布及其物理指标

本场地属西安市黄土梁，受隧道开挖所影响的土层分布及其物理指标见表1。

2 地表沉降监测与分析

测点布置总共分为 A、B、C、D四个断面，里程分别为 DK20+410、DK20+430、DK20+450、DK20+470。每个断面设八个测点，间距为5m。现以里程为DK20+450断面的监测数据来分析。

2.1 纵向地表沉降分析

隧道开挖采用短台阶法，上下导掌子面的开挖都会造成地层损失和扰动而引发地表沉降，见图2。从上下导掌子面与沉降的关系图来看，可分为四个阶段(L1、L2分别为上下导掌子面与监测断面的间距，D为隧道的跨度)。

1)当L1=-2D时，测点开始发生沉降，说明测点已进入受上导掌子面开挖的影响区。

2)当-2D≤L1≤1D时，L2＜-2D，此阶段的沉降表现为随上导掌子面不断向测点断面的逼近，沉降量不断增加，尤其是在通过断面前0.5D时，沉降值有一个陡增。在上导掌子面通过监测断面后相对于上导进尺的沉降速率已明显降低，沉降量趋向于稳定。说明上导已逐渐退出对该断面沉降的影响。当L1=1D时，沉降量为7.5 mm。

3)当L1＞1D时，-2D≤L2≤3D，此阶段相对于上导掌子面进尺的沉降速率较L2＜-2D时有显著的增长，说明下导掌子面的开挖已开始引起测点的沉降，沉降量又开始显著增加。

4)当L2＞3D时，沉降值很快趋于稳定，说明下导掌子面的开挖对测点沉降的影响已经消失。此时的沉降量为30 mm。

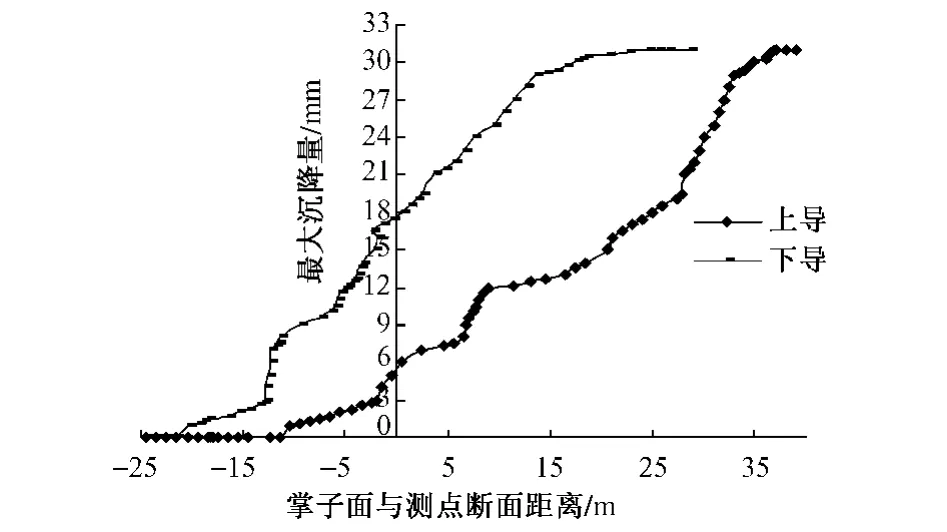
图2 上下导掌子面与沉降的关系

浅埋暗挖隧道台阶法施工时，上导对测点的影响范围为-2D～1D，下导对测点的影响范围为 -2D～3D。上导引起的沉降量要远远小于下导所引起的，其比值约为1/3。

2.2 横向地表沉降分析

2.2.1 横向沉降影响范围

隧道开挖对土体造成的扰动和破坏主要表现为由于开挖后的地层应力释放，周围重塑土为重新达到应力平衡和为了弥补地层损失所发生的地层移动。这就引发了一定范围内土体的整体移动变形，集中体现为地表横向沉降槽，见图3。

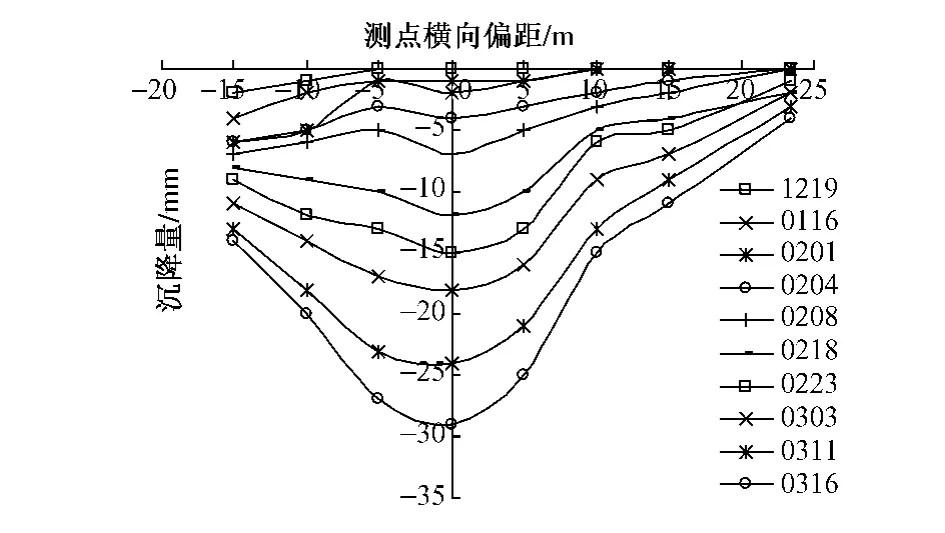
图3 地表横向沉降

图3表示了监测断面各测点的沉降值随隧道开挖的不断发展过程。在横坐标的负值区域由于有局部的杂填土，起始在固结作用下表现出相对较大的沉降量，随着隧道开挖的影响值越来越大，其固结沉降量可以忽略不计。从沉降曲线的轮廓来看，接近于正态分布，由对称性可以判别横向沉降槽宽度(沉降曲线对称中心到曲线拐点的距离)约为11 m。由于土层具有不同程度的湿陷性，其在降雨后的沉降也宏观表现为沉降，因此曲线拐点外侧的土体沉降量并没有很快地收敛。

2.2.2 Peck公式适用性的判定

1969年，Ralth Peck从当时得到的20多个隧道实例中总结出隧道的横向沉降槽曲线呈近似的正态分布(高斯曲线)。后来大量的实测数据也证实了其论断。Peck公式为

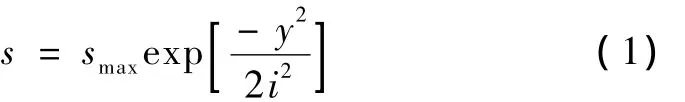
式中，s为地表任一点沉降量;smax为地表最大沉降量(对应于隧道轴线位置);y为沉降曲线中心到所计算点的距离;i为沉降槽的宽度，即沉降曲线对称中心到曲线拐点的距离。

韩煊、李宁等[9]在研究Peck公式在中国隧道的适用性时，通过对Peck公式进行变形，给出式(2)

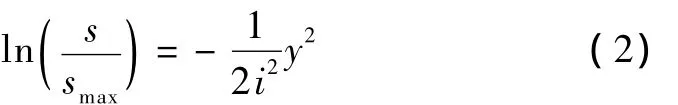
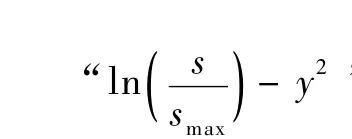
3 沉降槽宽度的确定

1982年，O’Reilly和 New[10]根据伦敦地区的经验，得出下式

式中，k为取决于不同土壤类型的沉降槽宽度系数;z0为隧道拱顶到地表的距离。O’Reilly和New后来又根据大量实测数据给出了以下经验公式

黏性土:

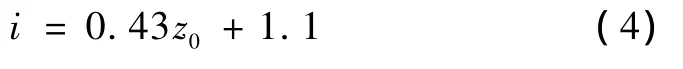
其他的研究者也证实黏性土的k值取值范围是0.4～0.5。

通过对所测数据做回归分析，可得回归直线斜率(见图 4)M=-0.003 7，又由式(4)有

图4 ln(s/smax)与y2关系的散点图及回归曲线

把图4中回归曲线的斜率M代入式⑸可得i=11.6，测点所在断面的平均埋深为16 m，代入式(3)可得k=0.66。

韩煊、李宁等通过对国内8个地区的多组观测数据的分析给出了我国部分地区沉降槽宽度参数初步建议值，见表 2[9]。

表2 我国部分地区沉降槽宽度参数k初步建议值

由表2可知本次观测值与建议值相对较大，其原因可能有①上层较厚杂填土疏密不均，监测期间存在固结沉降;②土层的厚薄不均加之湿陷性系数具有一定的差异性。由于样本数相对较少，监测值只能对本地区后续工程和类似土质具有参考意义。

图5为DK20+450断面实测沉降槽和其高斯拟合曲线的对比图。由图中看出两曲线能够较好地吻合，由于两侧土体的不均性使得拟合曲线的顶点稍微偏离于中轴线。

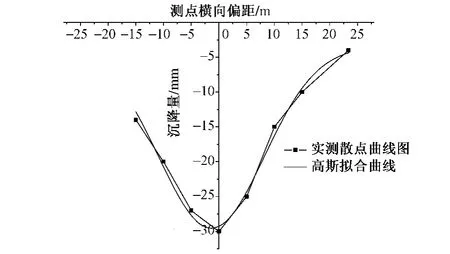
图5 DK20+450断面实测沉降槽和其高斯拟合曲线对比

4 结论

西安地铁会展中心站配线暗挖段区间属西安黄土梁，通过该浅埋暗挖隧道台阶法施工中洞开挖所引起的地表沉降数据进行分析，得出如下结论:

1)浅埋暗挖隧道台阶法施工时，上导对测点的影响范围为-2D～1D，下导对测点的影响范围为-2D～3D。上导引起的沉降量要远远小于下导所引起的。

2)采用台阶法施工，下导对沉降的影响量要大于上导引起的，由此在下导开挖后要在最短时间内施作初衬，使其尽快达到闭合结构，减少围岩的松动，减小沉降。

3)地表的横向沉降槽曲线符合Peck公式，且由此得出的沉降槽宽度i为11 m。当应用O’Reilly和New的经验公式时，可取沉降槽宽度参数k=0.66。

4)沉降槽可以用高斯曲线进行较好地拟合，但由于黄土的湿陷性系数和各地区土质的差异性，沉降槽宽度只能对类似土质具有参考意义。

[1]PECK R B. Deep excavations and tunnelling in soft ground[C]∥Proc.7th Int.Conf.SMFE.Mexico City:State of the Art Volume，1969:225-290.

[2]关宝树，国兆林.隧道及地下工程[M].成都:西南交通大学出版社，2002.

[3]姜德义，任松，刘新荣，等.隧道拱顶下沉时序遗传算法神经网络预测模型[J].地下空间与工程学报，2006，2:547-550.

[4]张顶立，黄俊.地铁隧道施工拱顶下沉值的分析与预测[J].岩石力学与工程学报，2005，24(10):1703-1707.

[5]钟有信，罗草原.浅埋暗挖地铁施工地层沉降监测与控制[J].西部探矿工程，2003，83(4):91-93.

[6]贾建波，焦苍，范鹏.天津地铁浅埋暗挖隧道地表变形分析[J].隧道建设，2006，26(1):18-20，24.

[7]吕勤，张顶立，黄俊.城市地铁暗挖施工地层变形机理及控制实践[J].中国安全科学学报，2003，13(7):29-34.

[8]姚永勤.钱仓山隧道地表沉降监测与分析[J].铁道建筑，2009(11):40-42.

[9]韩煊，李 宁，STANDING J R.Peck公式在我国隧道施工地面变形预测中的适用性分析[J].岩土力学，2007，28(1):23-28，35.

[10]O’REILLY M P，NEW B M.Settlements above tunnels in the United Kingdom——their magnitude and prediction[C]∥Proc. Tunnelling 82， Institution ofMining and Metallurgy，London，1982:173-181.

U451

A

1003-1995(2010)06-0058-04

2009-12-16;

2010-03-20

李辉(1963— )，女 ，河南洛阳人，副教授。

(责任审编 王天威)