球笼式等速万向节圆弧形沟道接触应力影响因素分析

汤双清，胡 欢，徐艳飞

(三峡大学 机械与材料学院，湖北 宜昌 443002)

符号说明

Dw——钢球直径，mm

Dpw——球组节圆直径，mm

E——弹性模量

E1——当量弹性模量

μ——接触体的泊松比

ε——第二类椭圆积分

k——接触椭圆系数

f——沟道曲率系数

Li，Le——星形套、钟形壳与钢球接触点的力臂，mm

p——接触应力

P0——沟道与钢球间的接触载荷，N

R1——圆弧沟道曲率半径，mm

∑R——主曲率半径和，mm

Rx,Ry——当量主曲率半径，mm

rax,ray——接触点钢球主曲率半径，mm

rbx,rby——接触点沟道主曲率半径，mm

T——万向节传递的扭矩，N·m

Z——钢球数

下标

i——内圈(星形套)沟道

e——外圈(钟形壳)沟道

球笼式等速万向节是目前应用最为广泛的等速万向节，作为前置前驱动轿车的关键部件，等速万向节的性能和寿命与接触应力密切相关，万向节疲劳破坏的特征通常是沟道表面产生剥落和麻点[1-2]。圆弧形沟道由于容易加工，且钢球和沟道只有两个接触点，不易出现“滞点”而被广泛使用。以下通过使用Hertz接触理论对球笼式等速万向节圆弧形沟道的接触应力进行参数化的公式推导，寻找出对万向节沟道接触应力有影响的参数。应用正交试验优化设计方法，将相应的影响参数选取为主要因素，并将其作为自变量设计正交化试验。对正交试验结果进行极差分析，得到3个主要因素对接触应力大小的影响程度。通过关注主要的影响因素，来指导圆弧形沟道等速万向节的设计生产加工，以便能有效减小沟道接触应力，从而增加其使用寿命。

1 圆弧形沟道接触应力的理论推导及影响因素

对等速万向节进行内部接触应力的理论分析，实际上是进行弹性接触分析，目前弹性接触分析主要采用的是Hertz接触理论。

1.1 结构参数的确定

圆弧截面形式的沟道是由一半径稍大于钢球半径的圆弧形成，如图1所示，以钢球球心为原点，建立平面直角坐标系，OO1为圆弧的圆心和钢球圆心之间的距离。

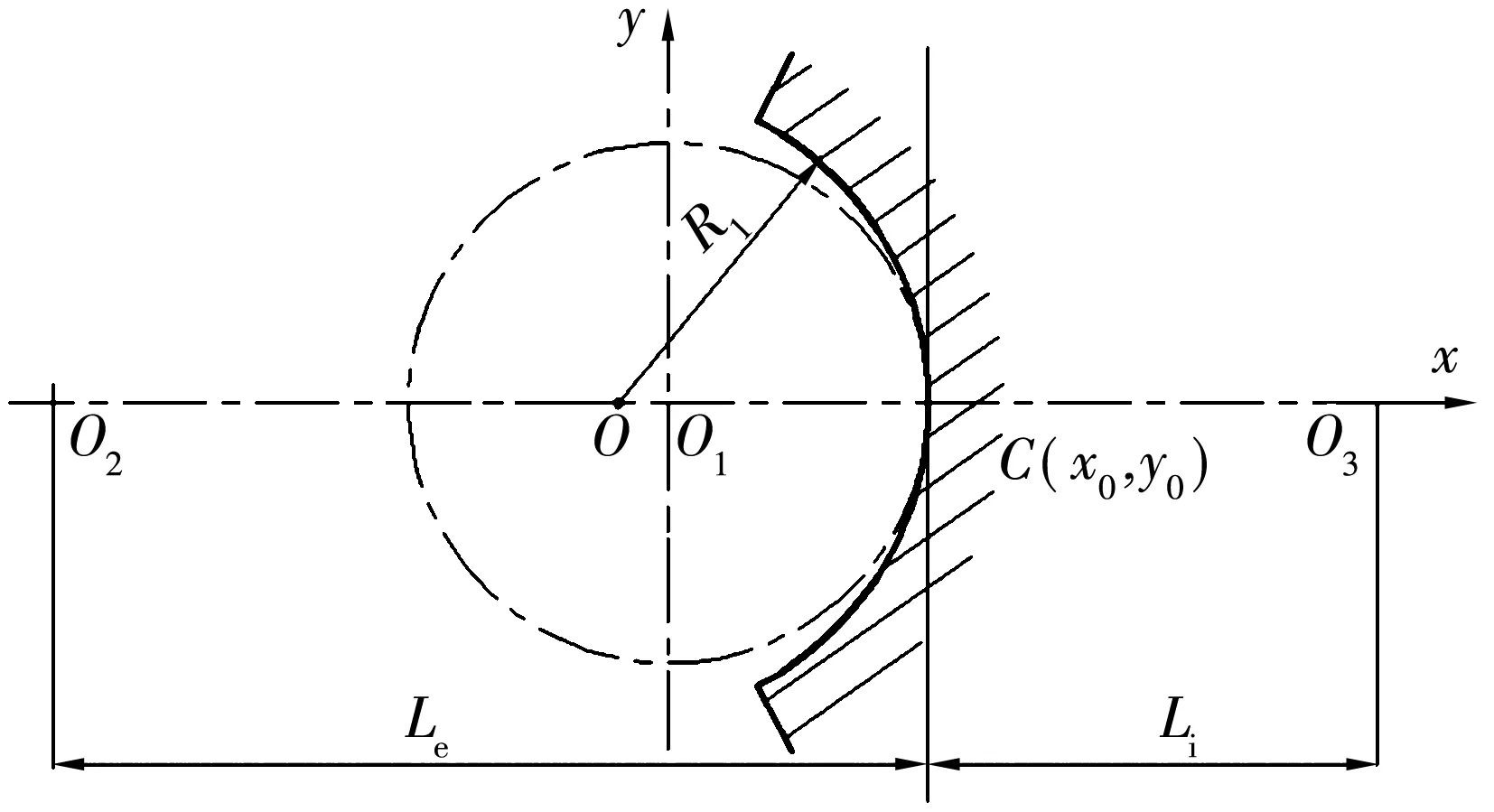
图1 圆弧沟道几何模型

(1)

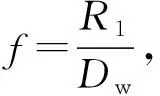
R1=fDw

(2)

由(2)式可得：

(3)

由此可知，圆弧沟道的结构参数OO1，R1仅同钢球直径Dw和接触点沟曲率系数f有关。

1.2 圆弧沟道主曲率半径和的确定

钢球与内圈接触主曲率可表示为：

(4)

rby=-R1=-fDw

同理,钢球与外圈接触主曲率可表示为：

(5)

rby=-R1=-fDw

引入当量主曲率：

(6)

(7)

主曲率和表示为：

(8)

则对于内沟道：

对于外沟道：

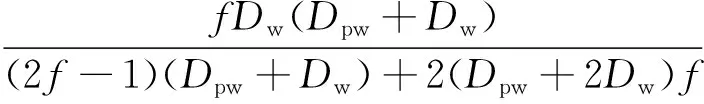
1.3 Hertz理论接触应力计算公式

根据文献[1]中的介绍，假定理想状态下作用在各球上的力相等，接触区处于弹性应力状态，且接触面尺寸比物体接触点曲率半径小得多。由此便可直接引用Hertz理论求解接触应力。

传递扭矩为T时6个钢球同时受载，理想状态下6个钢球上传递力的大小相同，此时作用在钢球与沟道接触点的接触载荷可表示为[4]：

(9)

(10)

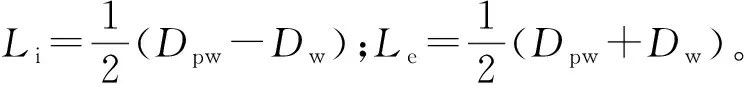
当接触点主曲率、法向载荷、弹性模量和泊松比已知时，用Hertz公式求得接触椭圆长、短半轴，进而可求得最大接触应力。

(11)

k和ε分别为椭圆系数和第二类椭圆积分，可分别由下式求得[4]：

1.4 沟道接触应力的影响因素

由上两节的公式推导可知，对圆弧形沟道接触应力有直接影响的参数为法向载荷P0、当量弹性模量E1、椭圆系数k、第二类椭圆积分ε以及接触点主曲率半径和∑R。当万向节的材料一定时，接触体的弹性模量和泊松比就一定，从而当量弹性模量E1一定；在钢球数Z=6及传递的扭矩T一定时，对法向载荷P0的影响参数为球组节圆直径Dpw和钢球直径Dw；椭圆系数k、第二类椭圆积分ε以及接触点主曲率半径和∑R都与球组节圆直径Dpw、钢球直径Dw以及沟道的沟曲率系数f有关，由此可知，圆弧形球笼式等速万向节沟道接触应力的主要影响因素为Dpw，Dw和f。

2 接触应力影响因素的正交试验优化设计

2.1 正交试验的因素与水平确定

对圆弧形球笼式等速万向节沟道接触应力有直接影响的结构参数为球组节圆直径Dpw、钢球直径Dw以及沟道的沟曲率系数f，故以这3个参数作为正交试验的因素，以沟道接触应力大小为正交试验的性能指标进行正交试验。

参照文献[3]中等速驱动轴的相关参数，选取球笼式等速万向节传递的最大转矩为T=1 122 N·m，所用钢球直径为Dw=15.875 mm，球组节圆直径为Dpw=54.3 mm，双心弧沟道和椭圆沟道与钢球接触角β=45°，圆弧形沟道沟曲率系数通常取f=0.505～0.520。钢球材料为GCr15，泊松比为μa=0.29，弹性模量为Ea=2.06×1011N/m2；钟形壳材料为55#钢，泊松比为μb=0.3，弹性模量为Eb=2.01×1011N/m2；星形套材料为20CrMnTi，泊松比为μc=0.29，弹性模量为Ec=2.06×1011N/m2。按照以上3个因素的取值，每个因素取3种水平，其正交试验的因素水平表如表1所示。

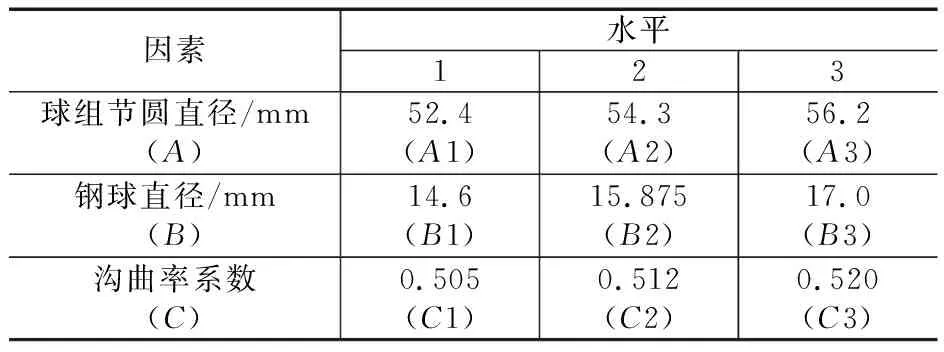
表1 接触应力正交试验优化设计因素水平表

2.2 正交试验方案组合及计算

因该正交试验有3个因素，每个因素都有3个水平，现选用L9(34)列出接触应力的正交试验方案表(表2)[5-7]。

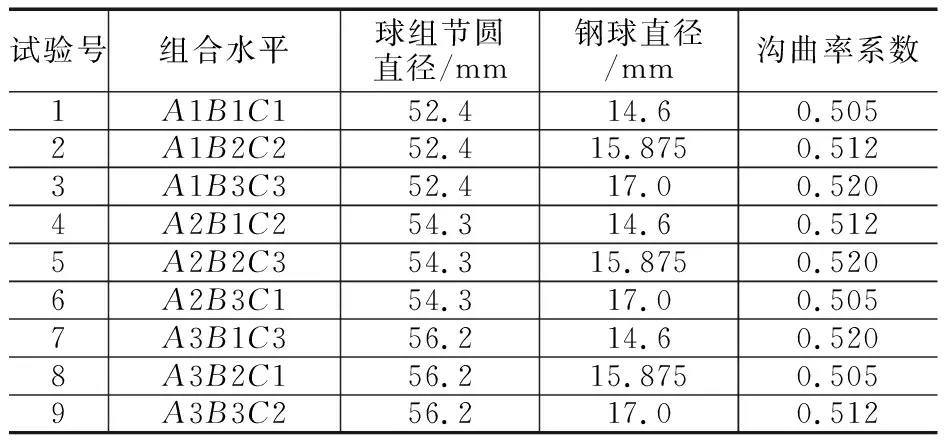
表2 接触应力正交试验方案组合表

根据上节中已知的各种参数及表2中对应的9组正交试验方案，由(11)式分别计算相应内、外沟道的接触应力，得出各试验的各项指标结果(表3)。

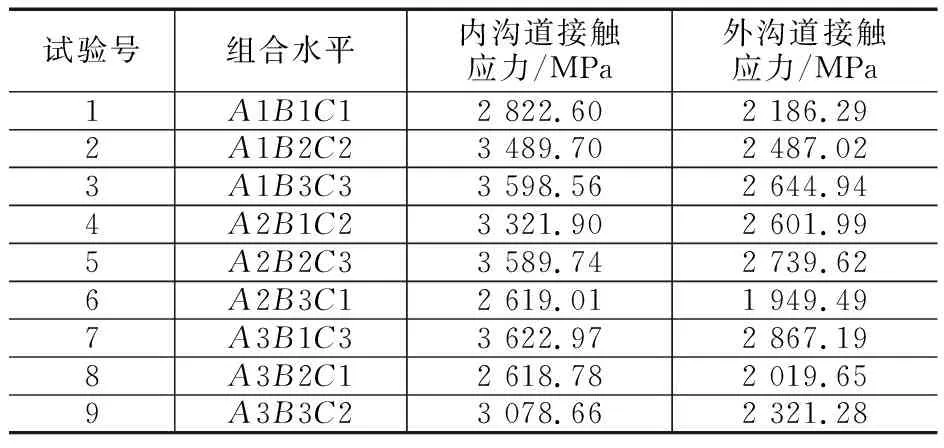
表3 各试验方案的指标结果

3 极差分析法分析

3.1 极差分析法计算

由表3的各列因素A，B，C分别计算每一种水平上试验值(接触应力性能指标)的平均数[5-7]。

即因素A在1，2，3水平上试验值的平均数分别为：

(1)对于内沟道

K1A=3 303.62；K2A=3 176.88；

K3A=3 106.80。

因素B在1，2，3水平上试验值的平均数分别为

K1B=3 255.82；K2B=3 232.74；

K3B=3 098.74。

因素C在1，2，3水平上试验值的平均数分别为

K1C=2 686.80；K2C=3 296.75；

K3C=3 603.76。

算出因素A,B,C的极差R(1，2，3水平中最大减最小的差)

RA=196.82；RB=157.08；RC=916.96。

(2)对于外沟道

K1A=2 439.42；K2A=2 430.37；

K3A=2 402.71。

因素B在1，2，3水平上试验值的平均数分别为

K1B=2 551.82；K2B=2 415.43；

K3B=2 305.24。

因素C在1，2，3水平上试验值的平均数分别为

K1C=2 051.81；K2C=2 470.10；

K3C=2 750.58。

算出因素A,B,C的极差(1，2，3水平中最大减最小的差)

RA=36.71;RB=246.58;RC=698.77。

3.2 各因素极差R主次关系比较分析

根据计算，对于内沟道：RC>RA>RB；对于外沟道：RC>RB>RA。

由上面的各因素极差值的比较可知：沟道的沟曲率系数对球笼式等速万向节内、外沟道接触应力的影响极为显著；而球组节圆直径和钢球直径的影响次之。

3.3 因素水平与指标关系图及试验分析

因素A实际水平为52.4，54.3，56.2 mm。以实际水平为横坐标，试验值(接触应力性能指标)平均数K1A，K2A，K3A为纵坐标，按照内、外沟道分别作图。对因素B、因素C也同样作图[5-7]，详见图2～图4。

图2 平均接触应力与A因素水平关系图

图3 平均接触应力与B因素水平关系图

图4 平均接触应力与C因素水平关系图

由以上平均接触应力与各因素水平关系图可知：在总体趋势上，内沟道接触应力大于外沟道接触应力与实际非常相符。图2中，内、外沟道的接触应力随着球组节圆直径的增大而减小。图3中，内、外沟道的接触应力也是随着钢球直径的增大而减小，这说明通过适当增大球组节圆直径和钢球直径，可以减小球笼式等速万向节内、外沟道的接触应力。但同时，球组节圆直径和钢球直径的增大，会使整个球笼式万向节尺寸增大，这又是不利的。图4中，随着沟曲率系数的增大，内、外沟道的接触应力增大，而且变化趋势较大，这也验证了沟曲率系数是影响圆弧形球笼式等速万向节内、外沟道接触应力最为显著的影响因素。减小沟曲率系数，可以显著地减小其内、外接触应力，从而增加其使用寿命。沟曲率系数的减小，意味着钢球和沟道的接触区域增大，这也对沟道的加工以及内部润滑及散热提出较高的要求。

4 结束语

通过使用Hertz接触理论公式及结构参数的推导，提出对圆弧形球笼式等速万向节内、外沟道接触应力大小有影响的3个因素——钢球回转直径、钢球直径以及沟道沟曲率系数，通过应用正交试验优化设计方法，验证了沟道沟曲率系数是影响圆弧形球笼式等速万向节内、外沟道接触应力最为显著的影响因素。通过适当控制沟道沟曲率系数大小，可以达到有效减小内、外接触应力，提高其性能及使用寿命的目的。