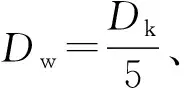七沟道球笼式等速万向节沟道接触应力的计算及优化设计

石宝枢，郭静芬

(1. 浙江众达传动股份有限公司，浙江 金华 321025；2. 洛阳轴研科技股份有限公司，河南 洛阳 471039；3.河南省高性能轴承技术重点实验室，河南 洛阳 471039；4.滚动轴承产业技术创新战略联盟，河南 洛阳 471039)

符号说明

dz—— 传动轴公称直径，mm

Dw——钢球直径，mm

Dpw—— 球组节圆直径，mm

Dk——钟形壳最大外径，mm

E0——钢球的弹性模量，MPa

E1——星形套的弹性模量，MPa

E2——钟形壳的弹性模量，MPa

Ei——星形套的当量弹性模量，MPa

Ee——钟形壳的当量弹性模量，MPa

Eki——星形套圆弧形沟道与相应钢球接触的第二类椭圆积分

Eke——钟形壳圆弧形沟道与相应钢球接触的第二类椭圆积分

fi——星形套圆弧形沟道截面曲率半径系数

fe——钟形壳圆弧形沟道截面曲率半径系数

KD——球组节圆直径系数

ki——星形套圆弧形沟道与相应钢球接触的椭圆系数

ke——钟形壳圆弧形沟道与相应钢球接触的椭圆系数

Li——星形套圆弧形沟道与相应钢球接触点距钢球回转中心的的距离，mm

Le——钟形壳圆弧形沟道与相应钢球接触点距钢球回转中心的的距离，mm

pimax——星形套圆弧形沟道与相应钢球的最大接触应力，MPa

pemax——钟形壳圆弧形沟道与相应钢球的最大接触应力，MPa

Qi——星形套圆弧形沟道与相应钢球的接触载荷，N

Qe——钟形壳圆弧形沟道与相应钢球的接触载荷，N

Ri——星形套圆弧形沟道截面曲率半径，mm

Re——钟形壳圆弧形沟道截面曲率半径，mm

∑Ri——星形套圆弧形沟道主曲率半径和，mm

∑Re——钟形壳圆弧形沟道主曲率半径和，mm

T——七沟道球笼式等速万向节所传递的转矩，N·mm

ν0——钢球材料的泊松比

ν1——星形套材料的泊松比

ν2——钟形壳材料的泊松比

球笼式等速万向节传递扭矩和旋转运动，通过位于星形套和钟形壳若干个素线为圆弧形的沟道和相同数量的一组钢球共轭接触而实现。星形套和钟形壳沟道与相应的钢球均承受接触载荷，故接触应力是决定球笼式等速万向节可靠性和寿命的重要因素。而星形套和钟形壳的沟道截面形状有圆弧、双偏心圆弧和椭圆等若干种，文中仅探讨圆弧形沟道截面。

七沟道球笼式等速万向节是该类产品技术的重要突破和优化设计的最终选择[1]，但仍需要对星形套和钟形壳圆弧形沟道与相应钢球的接触应力进行系统分析与定量计算，进而对2种圆弧形沟道的结构主参数进行优化，以进一步提高七沟道球笼式等速万向节的可靠性和寿命。

1 圆弧形沟道的曲率

沟道截面为圆弧形的星形套和钟形壳与相应钢球的接触如图1所示，O为钢球的中心，O1为星形套某沟道截面的曲率中心，O2为钟形壳某沟道截面的曲率中心，O3为星形套与钟形壳的球组节圆中心(钢球回转中心)。沟道截面的曲率半径与相应的钢球直径之比称为该沟道截面的曲率半径系数。

图1 球笼式等速万向节的圆弧形沟道

星形套圆弧形沟道截面曲率半径为

Ri=fiDw，

(1)

钟形壳圆弧形沟道截面曲率半径为

Re=feDw。

(2)

由图1可知，星形套、钟形壳圆弧形沟道与相应钢球接触点(沟道底部)距钢球回转中心的距离分别为

(3)

(4)

星形套、钟形壳圆弧形沟道的主曲率和分别为[2]

(5)

。(6)

2 接触应力计算

根据Hertz接触理论，假定理想状态下作用在每个钢球上的力均相等，接触区处于弹性应力状态，且接触点的尺寸比接触点的曲率半径小。

设七沟道球笼式等速万向节所传递的转矩为T， 7个均布且直径相等的钢球均同时受载。理想状态下7个钢球上传递力的大小均相等，则作用在星形套圆弧形沟道与相应钢球接触点的接触载荷为

(7)

钟形壳圆弧形沟道与相应钢球接触点的接触载荷为

(8)

当接触点的主曲率、法向载荷、弹性模量和材料的泊松比已知时，用Hertz接触理论可求得接触椭圆的长、短半轴，进而可求得最大接触应力[2]。

星形套圆弧形沟道与相应钢球的最大接触应力为

(9)

由(7)式、(9)式得星形套圆弧形沟道与相应钢球的最大接触应力为

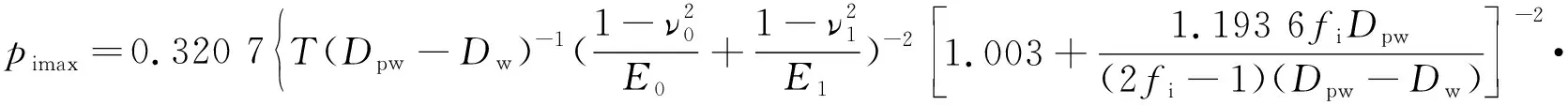
(10)

钟形壳圆弧形沟道与相应钢球的最大接触应力为

(11)

由(8)式、(11)式可得钟形壳圆弧形沟道与相应钢球的最大接触应力为

(12)

3 沟道结构主参数的正交试验及分析

3.1 正交试验方案及结果

由(10)式和(12)式可得，七沟道球笼式等速万向节星形套和钟形壳圆弧形沟道与相应钢球的接触应力(或承载能力)与钢球直径Dw、球组节圆直径Dpw、2种圆弧形沟道截面曲率半径系数fi(或fe)有关。星形套和钟形壳圆弧形沟道与相应钢球的最大接触应力pimax(或pemax)是以结构主参数Dw，Dpw，fi(或fe)为自变量的多元函数。要探讨的是自变量Dw，Dpw，fi(或fe)如何取值，使得pimax(或pemax)最小。为便于分析，分别取1个自变量(另2个自变量均视为常数)，分别探讨其对最大接触应力pimax(或pemax)的影响，即分别求pimax(或pemax)的方向导数。因(10)式、(12)式非常复杂，其变化规律难以用方向导数来表达。现参考文献[3]，通过正交试验探讨。

现以钢球直径Dw、球组节圆直径Dpw和沟道截面曲率半径系数fi(或fe)这3个参数为正交试验因素，以沟道最大接触应力值pimax(或pemax)为性能指标进行正交试验。

设某规格的七沟道球笼式等速万向节传递的最大转矩(静态额定转矩)T=1 887 N·m，Dw=17.463 mm，Dpw=60 mm，星形套和钟形壳圆弧形沟道截面曲率半径系数为fi=fe=0.515；钢球材料为GCr15，E0=206 GPa，ν0=0.29；星形套材料为20CrMnTi，E1=206 GPa，ν1=0.29；钟形壳材料为55#钢，E2=206 GPa，ν2=0.30。

每个因素取3种水平，其正交试验的因素与水平见表1。正交试验组合方案及计算结果见表2。

表1 沟道接触应力正交试验优化设计因素与水平

由表2的各列因素A，B，C，可分别计算出星形套、钟形壳沟道接触应力每种水平试验值的平均值及极差，结果见表3。

表2 沟道接触应力正交试验及计算结果

表3 沟道接触应力平均值及极差

3.2 极差分析

星形套和钟形壳沟道截面曲率半径系数fi(或fe)的极差远大于钢球直径Dw和球组节圆直径Dpw的极差。由此可见，星形套和钟形壳沟道截面曲率半径系数对七沟道球笼式等速万向节沟道的接触应力(或承载能力)的影响极其显著，远远大于钢球直径和球组节圆直径的影响。

3.3 试验分析

接触应力平均值与主参数的关系如图2～图4所示。

图2 接触应力平均值与钢球直径的关系

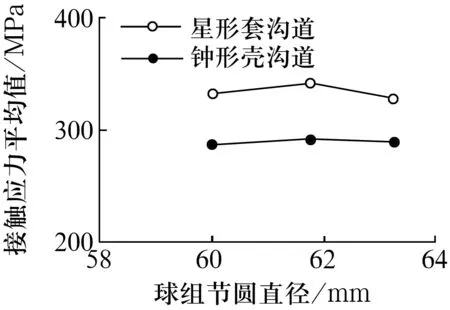
图3 接触应力平均值与球组节圆直径的关系

图4 接触应力平均值与沟道截面曲率半径系数的关系

由图可知，星形套沟道的接触应力总大于钟形壳沟道的接触应力(或承载能力),即钟形壳的承载能力总大于星形套的承载能力，星形套是薄弱环节。现分别讨论3个结构主参数对七沟道球笼式等速万向节的接触应力的影响。

3.3.1 钢球直径

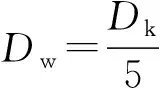
3.3.2 球组节圆直径

由表2和图3可知，球组节圆直径越大，星形套和钟形壳的接触应力越小，承载能力越大。但接触应力和承载能力的变化幅度较小，若球组节圆直径增加5%，承载能力约提高1.5%。显然，适当增大球组节圆直径能提高七沟道球笼式等速万向节承载能力和寿命。同样球组节圆直径Dpw不宜过大，经计算Dpw=KD(Dk+dZ)(KD=0.54～0.55)，或者Dpw=3.5Dw为最优。

3.3.3 沟道截面曲率半径系数

由表2和图4可知，星形套和钟形壳沟道截面曲率半径系数越小，星形套和钟形壳的接触应力越小，承载能力越大,且接触应力和承载能力的变化幅度大，若星形套和钟形壳沟道曲率半径系数减小1%，承载能力约提高60%。由此可见，适当减小星形套和钟形壳沟道截面曲率半径系数，可显著地提高七沟道球笼式等速万向节的承载能力。星形套和钟形壳沟道曲率半径系数为0.505是七沟道球笼式等速万向节优化设计的结果。

4 结论

1)七沟道球笼式等速万向节的承载能力和寿命与钢球直径、球组节圆直径、星形套和钟形壳沟道截面曲率半径系数均有关。

2)七沟道球笼式等速万向节星形套沟道的接触应力总是大于钟形壳的接触应力，即钟形壳承载能力大于星形套的承载能力。