钢球硬磨加工工艺的优化
2010-07-31傅蔡安
傅蔡安,张 韬,薛 喆
(江南大学 机械工程学院,江苏 无锡 214122)
1 钢球硬磨的成球机理
钢球硬磨加工的目的是去除前道工序的表面缺陷和在热处理时产生的脱碳、氧化层及表层屈氏体组织,进一步提高尺寸精度、球形精度和表面质量,为后续的研磨工序作准备。
1.1 硬磨成球的基本条件
在硬磨过程中,虽然磨削质量受诸多因素的影响,但钢球成圆的基本条件可以总结为以下两点[1]:
(1)切削等概率性,即钢球表面上每个点都有相同的切削加工概率。
(2)磨削尺寸选择性,即加工过程中, 应该磨尺寸大的球而不磨或少磨尺寸小的球; 磨长轴方向, 不磨或少磨短轴方向。
钢球硬磨加工设备都以提高这两个条件的显著性为目标。
1.2 现有硬磨机床的成球机理
目前我国使用的钢球硬磨机床,一般采用循环磨削方法(图1)。加工时,钢球装入料盘中,随料盘转动钢球从固定盘进料槽口,经流球板进入滚道,在砂轮与固定盘之间进行硬磨加工,磨完一圈后,再从出料槽口流出,重新回到料盘。这种循环磨削方法,使每粒钢球进入磨削滚道的次数和时间尽可能地相同。

图1 钢球硬磨示意图
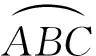

图2 钢球硬磨原理图
2 现有硬磨加工工艺中存在的问题
为了更好地分析钢球的磨削过程,建立了钢球硬磨时的运动学模型。
2.1 运动学模型
建立钢球的硬磨运动学模型如图3所示,应用刚体运动学普遍定理[2],建立方程:
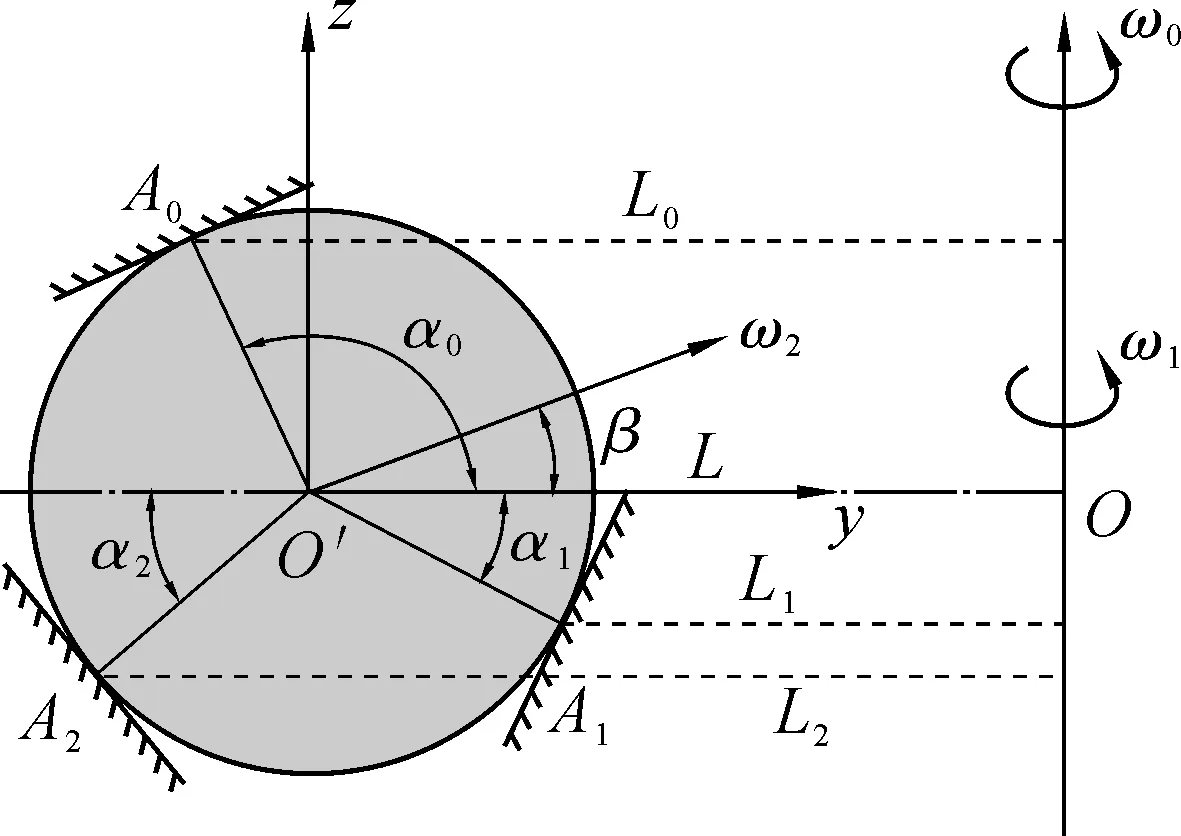
图3 钢球硬磨运动学模型
(1)
(2)
联立(1)式和(2)式,得到解析式:
(3)
(4)
式中:L,L0,L1,L2分别为O′,A0,A1,A2的公转半径;α0,α1,α2为A0,A1,A2与相应轴的夹角;β为ω2矢量与直线O′O所夹锐角。

2.2 工艺分析


图4 平面砂轮


图5 固定盘开沟槽的砂轮模型
由分析可知,现有硬磨机由于枢转运动不明显,很难保证钢球的成圆基本条件。此外,现有加工过程中,由于钢球在砂轮滚道内一次磨削的有效磨削量有限,且加工参数(工作推力、磨削点的位置等)不尽合理,造成较高的空耗,存在着效率低、能耗高等问题。
3 钢球硬磨加工的动力学模型
加工过程中,砂轮对钢球的磨削力对钢球的加工精度和效率的影响不能忽视,为了更好地分析硬磨机理,在引入磨削力下,建立硬磨加工的动力学模型。
3.1 动力学模型
根据磨削力的公式[4],取砂轮对钢球的包络角中的一小段为dθ(图6),得到钢球磨削时微弧段dθ对应的法向磨削力Fn和切向磨削力Ft:
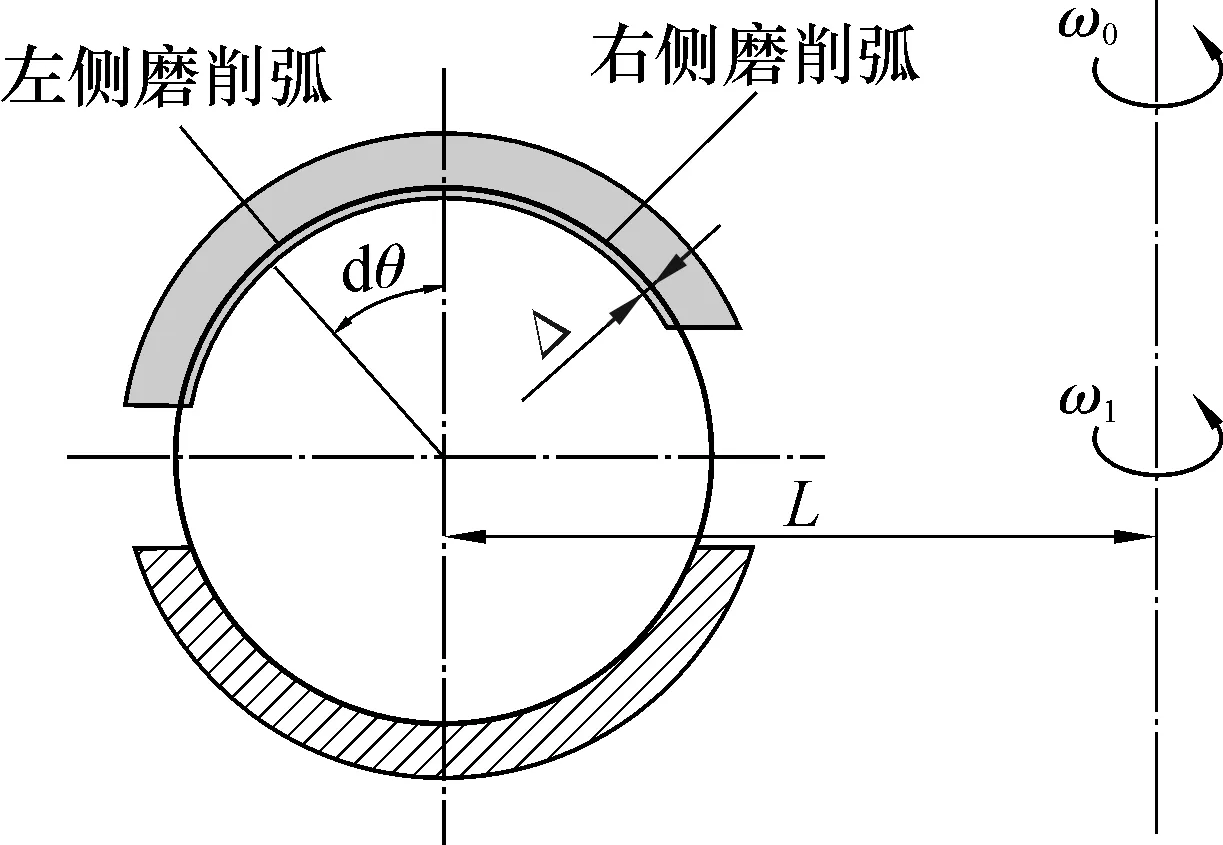
图6 磨削力分析图
(5)
(6)
式中:Δ为钢球在砂轮包络弧段内的平均径向切入量;Cp为比磨削力;摩擦系数μ=2μ′/πcscφ,μ′为砂轮的磨粒与钢球间的摩擦系数;2φ为磨粒切削刃前端角;v2为切入点钢球磨削的进给速度,当磨削点位于砂轮左侧磨削弧时,v2左=ω3Rcosθ+ω4Rsinθ,当磨削点位于砂轮右侧磨削弧时,v2右=ω3Rcosθ-ω4Rsinθ;(ω0-ω1)L为切入点砂轮与钢球球心间的相对速度。

图7 锥形砂轮的受力分析
由于砂轮半径L远大于钢球的半径R,钢球受到的离心力很小,对钢球的硬磨运动影响不显著,因此假设钢球在直的圆弧轨道中运动,钢球列部分平衡方程为:
(7)
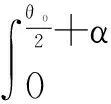
(8)
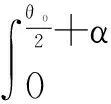
(9)
式中:Fn左(Fn右),Ft左(Ft右)为左(右)侧磨削弧中的微弧段dθ对应的法、切向磨削力;FMy为分布于磨削弧上的切向磨削力的合力;MMz为分布于磨削弧中磨削力对z轴的力矩。
将(8)式,(9)式代入(7)式得到:
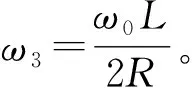
(10)
3.2 动力学模型分析
3.2.1 影响枢转速度ω4的因素

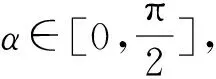

图8 枢转速度与砂轮偏角的关系(L=300 mm)
3.2.2 影响推力P的因素
P为主轴方向径向磨削力Fn的分力,即:
cos 2α+θ0)+ω4sinθ0sin 2α]
(11)


图9 推力与砂轮偏角关系图(Δ=5×10-4 mm)
4 内凹锥形砂轮的设计
由上述分析可知,枢转ω4、推力P等与砂轮偏角α密切相关,因此,设计砂轮截面形状为内凹锥形(图10),以提高磨削精度和效率。

1—内凹锥形砂轮;2—砂轮衬板;3—螺栓;4—主轴;5—轴承;6—轴承盖;7—砂轮基座;8—钢球;9—固定盘衬板;10—固定盘基座;11—固定盘图10 内凹锥形砂轮磨削示意图
4.1 内凹锥形砂轮对加工精度的影响
根据上述推导计算,将平面砂轮改为锥度为20°的内凹锥形砂轮。此时加工半径为5 mm的钢球,ω4可提高至1 241.4 r/min(130 r/s);若锥度增大为38°,ω4可提高至2 387.3 r/min(250 r/s),但砂轮偏角过大会使钢球的有效磨削弧长度减少,影响钢球的硬磨效率和砂轮的强度。实际生产中,砂轮偏角的取值为[0°,20°],可显著提高钢球表面各个质点切削等概率性,改善钢球的球形精度。
4.2 内凹锥形砂轮对推力P的影响
实际加工中,机床对砂轮的推力P并非越大越好,其对提高磨削质量或效率并无影响,反而使机床受力,增加能耗,使砂轮在B点附近的压强增加(图2),磨粒的无效挤压破损增大。由图9可知,在Δ不变的条件下,推力P会随α的增大而减小,这说明适当增大砂轮偏角可保护机床并降低能耗。
4.3 内凹锥形砂轮对加工效率的影响
钢球硬磨加工的磨削效率是指单位时间内钢球表面余料的去除量,理想状况下,可认为钢球表面通过磨削弧,该层金属即被去除,因此,磨削效率与钢球的进给速度v2成正比。设磨削效率为W,则:

(12)
根据(12)式,利用MATLAB,得到磨削效率与砂轮偏角α之间的关系曲线,如图11所示。由图可知,α在0~20°,磨削效率W随α的增加而增大,在α=20°时,W为最大;当α>20°时,W随α的增加而急剧减小。显然砂轮偏角为20°时,钢球硬磨有较好的成球精度和磨削效率。

图11 磨削效率与砂轮偏角的关系
4.4 内凹锥形砂轮的修整
内凹锥形砂轮的修整仍采用现有硬磨机床的金刚石修整器,但在安装时须将修整器的金刚石面与砂轮锥面平行,以保证砂轮面为锥面。
5 结束语
通过建立钢球硬磨的运动学和动力学模型,从理论上分析了现有硬磨加工存在的不足、影响硬磨精度和效率的主要因素。设计了内凹锥形结构砂轮,并得出了当内凹锥形砂轮的偏角为20°时,既可提高钢球的球形精度,又可提高钢球的磨削效率;同时在磨削深度不变的情况下,内凹锥形砂轮可使机床提供的轴向推力减小,减少了能耗。
