谐波及无功电流检测低通滤波器的优化设计方法

王少杰 ，罗安，孙贤大

(1. 湖南大学 电气与信息工程学院，湖南 长沙，410082；2. 邵阳学院 电气与信息工程系，湖南 邵阳，422000)

谐波和基波无功功率的信息是通过一定的检测方法获得的，以此作为参考来控制有源滤波器[1-3]的输出，因此，这种方法又称为谐波和基波无功参考电流或参考电压的获取方法。该方法的效果在很大程度上决定了有源滤波器的工作性能。最早的检测方法是通过模拟电路实现的，随着电子技术和计算机的飞速发展，谐波和基波无功的检测[4-7]也被数字检测方法所替代。三相电路瞬时无功功率理论[8-12]首先于1983年由赤木泰文提出。它突破了传统的以平均值为基础的功率定义，系统定义了瞬时无功功率、瞬时有功功率等瞬时功率。以此为基础可以得出用于有源电力滤波器的谐波和无功电流的实时检测方法。这些方法具有物理概念明确、计算量少、实时性强等优点。本文作者针对电网中谐波电流的特点，对谐波和无功电流检测中的低通滤波器进行优化设计，以便提高检测精度和响应速度。

1 ip-iq法检测谐波和基波无功功率的基本原理

设三相瞬时电压为：

其中：ia，ib和ic分别为A相、B相和C相瞬时电流；Em为最大电压；ω0为角频率。通过三相至两相的坐标变换，把ia，ib和ic变换到两相坐标系上，得到α相和β相的电压eα和eβ以及电流iα和iβ。α-β坐标系如图1所示。

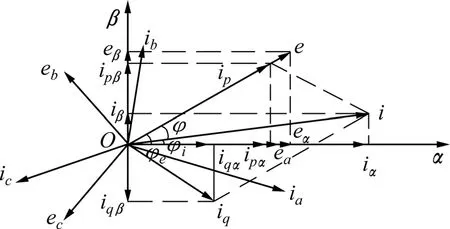
图1 α-β坐标系和a-b-c坐标系Fig.1 α-β coordinate system and a-b-c coordinate system

定义α-β坐标系下瞬时有功功率为：

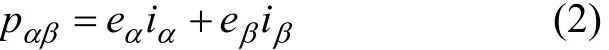
定义α-β坐标系下瞬时无功功率为：

即

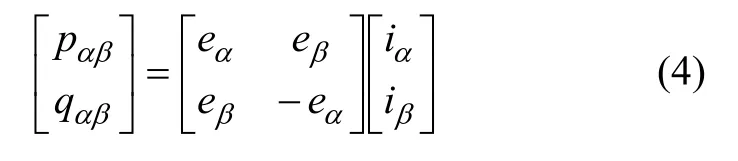
当ea，eb，ec，ia，ib和ic均为标准正弦波时，pαβ与平均有功功率P相等，而qαβ和平均无功功率Q相等。在ip-iq法中，采用跟eα和eβ相位相同的单位正弦函数来代替eα和eβ，这时，式(4)中的pαβ和qαβ转变为电流矢量在电压矢量及其法线上的投影，定义为ip和iq。

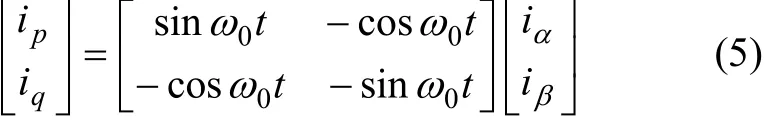
式中：0ω为基波角频率。这时，ia，ib和ic中基波分量所对应的瞬时有功电流ifp及瞬时无功电流ifq为常数，而高次谐波所对应的瞬时有功电流ihp及瞬时无功电流ihq则为交变量，可以通过 1个低通滤波器从ip和iq中分离出由式(4)可知：

此时，在a-b-c坐标系下的基波电流分量为：

通过三相电流瞬时值减去三相基波电流可以得到三相瞬时谐波电流。采用ip-iq法检测电网谐波电流的检测流程如图2所示。其中：

图2 ip-iq法检测电网谐波电流的检测流程Fig.2 Process of ip-iq harmonic detection in grid

2 ip-iq谐波检测方法的频域分析

ip-iq谐波检测方法是基于时域分析的，而谐波检测算法的性能需要通过其频域分析得出。对整个系统进行闭环控制时，也需要得出检测环节的传递函数，得到其增益以及相位曲线，因此，有必要对ip-iq谐波检测方法进行频域分析[13]。

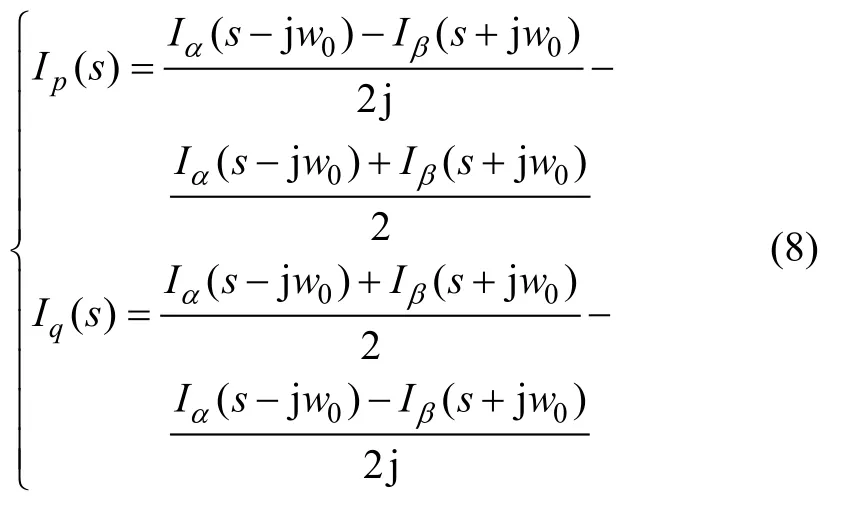
LPF的传递函数GLPF(s)为：

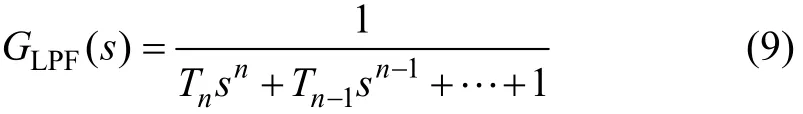
则ip和iq滤波后的直流分量

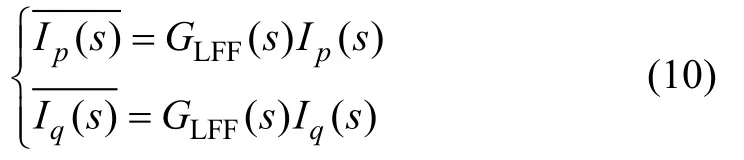
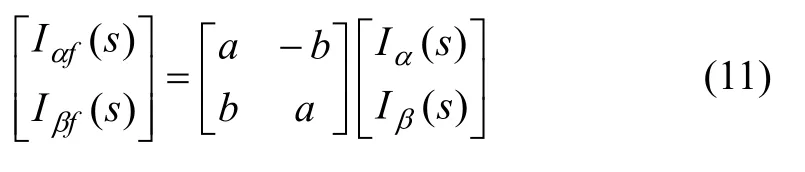
再经坐标变换得到谐波电流分量为：

假设三相对称，且

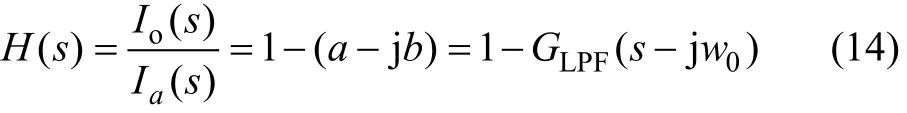
则可以得到输入信号I(s)到Io(s)的传递函数H(s)为：因为对于低通滤波器，GLPF(0)=1，所以，H(s)可以看成1个陷波器，ip-iq谐波检测算法的实质是通过坐标变换将低通滤波器GLPF(s)转换成陷波器H(s)，陷波器的中心频率为w0即基波频率，H(s)滤掉输入信号的基波分量后，就可以得到其谐波分量。不直接使用陷波器是因为陷波器存在差分效应，设计比较困难，容易受到干扰。低通滤波器GLPF(s)的性能直接决定着检测方法的精确性和动态跟踪速度，并最终影响有源电力滤波器的谐波补偿性能。

3 低通滤波器的设计

付青等[14]提出了将1个陷波器与1个高截止频率的低通滤波器串联的方式来设计低通数字滤波器，这样做可以有效地协调检测精度与速度的矛盾，但是，陷波器存在差分效应，较难稳定。袁兆祥等[15]提出了将低通滤波器与均值滤波器串联的思想，其中，均值滤波器可理解为 1种N阶的有限冲激响应(Finite impulse response，FIR)滤波器，具有很高的检测精度，而且实现比较方便，但是，需要检测1个周期的信号才能得到结果，有1个周期延时，响应较慢。本文综合上述2种方法的优点，针对电网谐波电流主要为奇次谐波的特点，对文献[15]中方法进行改进，结构与其基本相同，只是将其中的均值滤波器改为N/2阶，从而将延时减少到半个周期，提高响应速度，而后面串联的低通滤波器可以选择较高的截止频率。其设计过程如下。

3.1 均值低通滤波器的设计

三相电网电流ia，ib和ic中的n次正序和n次负序谐波分量，经过三维坐标abc→二维坐标pq变换后，分别转化为ip和iq中的(n-1)次和(n+1)次谐波分量。ip和iq中的直流分量对应的就是基波正序电流分量，而ip和iq中的交变分量对应的就是负序和谐波电流分量。电网谐波电流中主要成分为奇次谐波，这些奇次谐波经过坐标变换后在ip和iq中为偶次谐波。当电网最低次谐波为3次谐波时，ip和iq中的交流分量最低频次为2次(100 Hz)。

对于ip和iq的周期信号，通过均值滤波器可以得到有效滤除。设电网基波频率为f0，每个周期采样N点，即采样频率为Nf0，因为其主要为偶次成分，没有必要进行N点均值滤波，进行N/2点均值滤波即可，则

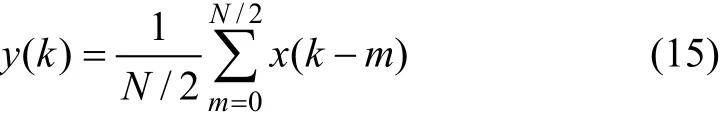
可以看出：它实际上是1种N/2阶的FIR滤波器，将其写成差分形式得：

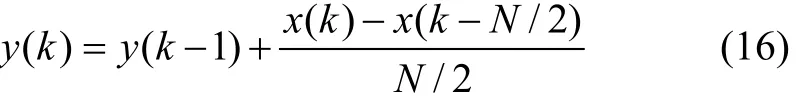
实际中，f0=50 Hz，1个周期采样128点，采样频率为6.4 kHz，利用Matlab可以获得其频域特性曲线和阶跃响应曲线，如图3和图4所示。

图3 均值滤波器的幅频特性Fig.3 Amplitude-frequency of average low-pass filter

图4 均值滤波器的阶跃响应Fig.4 Step response of average low-pass filter

由图3和图4可以看出：均值滤波器对于ip和iq中的偶次谐波成分可以得到有效衰减，衰减幅度超过80 dB，延时为半个周期(约10 ms)。

3.2 ButterWorth低通滤波器的设计

均值滤波器能对ip和iq的偶次谐波成分衰减，与之串联的低通滤波器主要实现2个功能：一是对其中的奇次成分进行衰减；二是当采样频率有所偏差时，导致均值滤波器性能提高。因为均值已经将 100 Hz信号滤除，需要滤除信号的最低频率为150 Hz，所以，低通滤波器的截止频率可以较高。

由于LPF的目的是获取电流直流分量ip′和iq′，而LPF的相位特性对直流量的检测没有任何影响。在实际工程应用中，通常选用 IIR滤波器。与其他的 IIR滤波器相比，ButterWorth低通滤波在线性相位、衰减斜率和加载特性3个方面具有特性均衡的优点，因此，在实际使用中选ButterWorth滤波器。仿真结果如图5和图6所示。

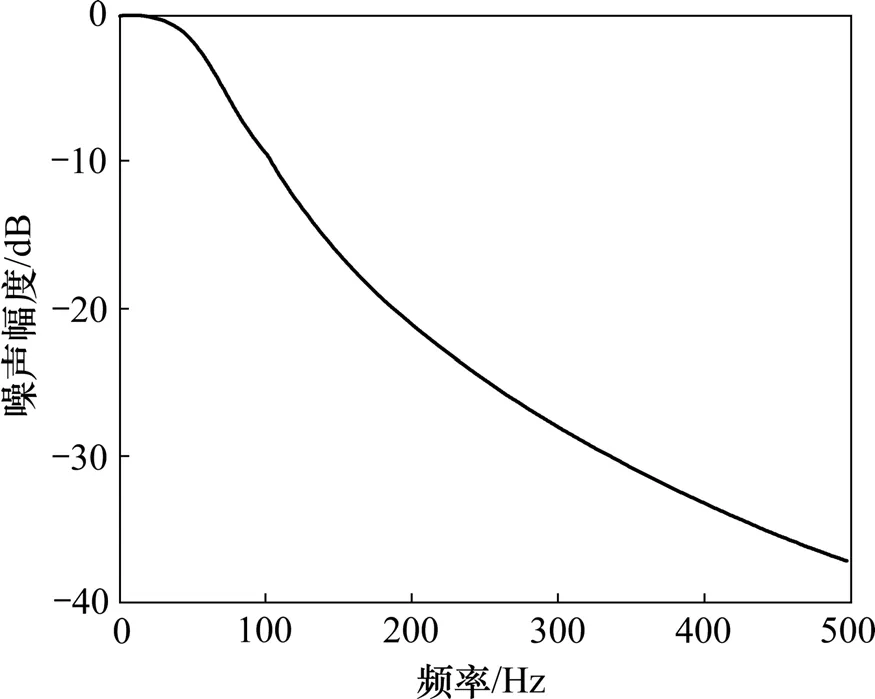
图5 ButterWorth滤波器的幅频特性Fig.5 Amplitude-frequency of ButterWorth filter

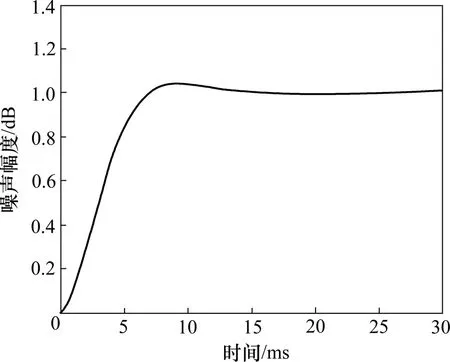
图6 ButterWorth滤波器的阶跃响应Fig.6 Step response of ButterWorth filter

由图5和图6可以看出：ButterWorth滤波器对最低频次150 Hz的噪声衰减幅度为16 dB，响应时间为7 ms左右。

3.3 新型滤波器的设计

将前面所设计的 ButterWorth滤波器与均值滤波器串联后就可以得到新型滤波器，利用Matlab可以作出其幅频特性和阶跃响应曲线，如图7和图8所示。

图7 新型滤波器的幅频特性Fig.7 Amplitude-frequency of novel filter

图8 新型滤波器的阶跃响应Fig.8 Step response of novel filter

由图7可知：新型滤波器具有与均值滤波器一样的性能，对偶次谐波进行了很大衰减，奇次谐波中衰减频率最低的为150 Hz，其噪声衰减幅度为30 dB；随信号频率的增加，滤波器对信号的衰减逐渐加大。所以，通过该检测滤波器就可使基波成分所对应的直流分量通过，而使谐波所对应的交流分量被有效滤除。由图8可知：新型滤波器的响应时间约为16 ms，具有较快的响应速度。

4 仿真

基于上面设计出来的新型低通滤波器，利用Matlab对ip-iq谐波检测算法进行整体仿真，仿真时输入信号源如下：

采用文中设计的新型检测滤波器检测该三相电流中的谐波成分，仿真结果如图9所示，其中：图9(a)所示为检测出来的基波有功电流波形，检测结果为171.4 A，与理论结果140× 3/2=171.5接近；图9(b)所示为检测出来的基波无功电流波形，检测结果为0，理论计算的结果为 0，二者相等。检测出来的谐波电流信号和输入的谐波信号在稳态时二者几乎重叠，这说明这种具有很高的稳态精度。由图 9(a)可知：系统的响应时间约为 16 ms，主要是均值滤波器和ButterWorth低通滤波器的延时，与FFT算法相比，其响应速度较快。

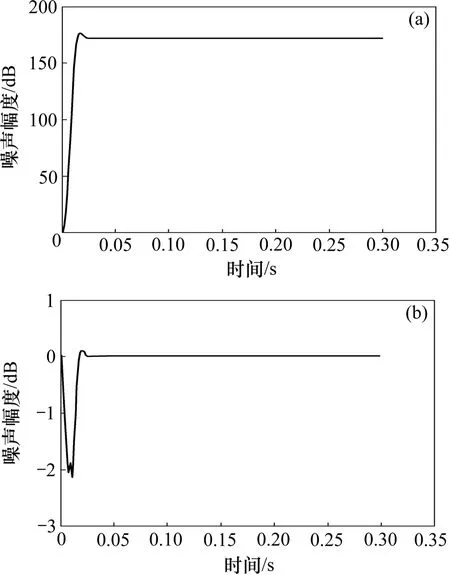
图9 仿真波形Fig.9 Simulation waveforms

5 结论

(1)将N/2阶的均值滤波器和二阶巴特沃斯低通滤波器进行结合的新型滤波器，可使基波成分所对应的直流分量通过，有效滤除谐波所对应的交流分量。

(2)采用新型滤波方法，能够使谐波和无功电流检测中的低通滤波器响应时间缩短，提高检测的响应速度，同时还能够提高稳态精度。

[1] 罗安. 电网谐波治理和无功补偿技术及装备[M]. 北京: 中国电力出版社, 2006: 1-20.LUO An. Harmonic control and reactive power compensation of the grid and its equipments[M]. Beijing: China Electric Power Press, 2006: 1-20.

[2] Detjen D, Jacobs J, De Doncker R W, et al. A new hybrid filter to dampen resonances and compensate harmonic currents in industrial power systems with power factor correction equipment[J]. IEEE Trans on Power Electronics, 2001, 16(6):821-827.

[3] Singh B, Al-Haddad K, Chandra A. A review of active filters for power quality improvement[J]. IEEE Trans on Industrial Electronics, 1999, 46(5): 1-12.

[4] 李江, 孙海顺, 程时杰, 等. 基于灰色系统理论的有源滤波器的预测控制[J]. 中国电机工程学报, 2002, 22(2): 6-10.LI Jiang, SUN Hai-shun, CHENG Shi-jie, et al. Prediction control of active power filter based on the grey theory[J].Proceedings of the CSEE, 2002, 22(2): 6-10.

[5] 邓文浪, 杨欣荣, 朱建林, 等. 改进矩阵变换器在输入电压非正常情况下的调制策略[J]. 控制与决策, 2006, 21(8): 908-912.DENG Wen-lang, YANG Xin-rong, ZHU Jian-lin, et al.Improvement of modulation strategy for matrix converter under abnormal input voltages[J]. Control and Decision, 2006, 21(8):908-912.

[6] 夏向阳, 罗安. 自适应频率跟踪的谐波电流检测方法[J]. 高电压技术, 2008, 34(8): 1715-1721.XIA Xiang-yang, LUO An. Novel method for measuring harmonic current based on adaptive frequency-tracking[J]. High Voltage Engineering, 2008, 34(8): 1715-1721.

[7] 唐欣, 罗安, 谭甜源. 有源电力滤波器的比例递推积分控制[J]. 控制理论与应用, 2004, 21(4): 631-634.TANG Xin, LUO An, TAN Tian-yuan. Active power filter with a proportional recursive integral controller[J]. Control Theory &Applications, 2004, 21(4): 631-634.

[8] 刘开培, 张俊敏, 陈艳慧. 基于重采样的三相谐波检测瞬时无功功率法[J]. 电力系统自动化, 2003, 27(12): 45-47.LIU Kai-pei, ZHANG Jun-min, CHEN Yan-hui. Instantanelous harrmonics detecting method for three-phase circuits based on resampling[J]. Automation of Electric Power Systems, 2003,27(12): 45-47.

[9] 蒋斌, 颜钢锋, 赵光宙. 单相电路瞬时谐波及无功电流实时检测新方法[J]. 电力系统自动化, 2000, 11(21): 35-39.JIANG Bin, YAN Gang-feng, ZHAO Guang-zhou. A new method for real-time detecting harmonics and reactive currents in single-phase circuit[J]. Automation of Electric Power Systems,2000, 11(21): 35-39.

[10] LUO Shi-guo, HOU Zheng-cheng. An adaptive detecting method for harmonic and reactive current[J]. IEEE Trans on Industrial Electronics, 1995, 42(1): 85-89.

[11] Kim H, Blaabjerg F, Bak-Jensen B, et al. Instantaneous power compensation in three-phase systems by usingp-q-rtheory[J].IEEE Trans on Power Electronics, 2002, 17(5): 701-710.

[12] Bojyup M, Karlsson P, Alakula M, et a1. A multiple rotating integrator controller for active filters[C]//Proceedings of EPE Conference. l999: 103-110.

[13] TONG Li-qing, QIAN Zhao-ming, KUANG Nai-xing, et al.Optimal design of synchronous reference frame harmonic detection method[J]. IEEE Trans on Industrial Electronics, 2007,7(2): 1071-1076.

[14] 付青, 罗安, 刘宇. 一种瞬时功率理论谐波检测的低通滤波器设计新方法[J]. 湖南科技大学学报, 2005, 20(1): 62-66.FU Qing, LUO An, LIU Yu. A novel design of the low-pass filter in the harmonic detecting method based on the instantaneous reactive power theorem[J]. Journal of Hunan University of Science & Technology, 2005, 20(1): 62-66.

[15] 袁兆祥, 郑建勇, 胡敏强, 等. 有源滤波器中新型检测滤波器的设计[J]. 中国电机工程学报, 2008, 28(9): 45-49.YUAN Zhao-xiang, ZHENG Jian-yong, HU Min-qiang, et al.Design of a novel detection filter of active power filter[J].Proceedings of the CSEE, 2008, 28(9): 45-49.