基于PFC-(PID-H∞)300 MN模锻水压机动梁速度跟踪控制
2010-07-31黄长征谭建平
黄长征,谭建平
(1. 韶关学院 机电工程系,广东 韶关,512005;2. 中南大学 机电工程学院,湖南 长沙,410083)
300 MN模锻水压机是当前亚洲最大的模锻液压机,是我国国防和基础建设的关键设备。速度控制技术是其关键技术之一,在等温锻压或模拟等温锻压中必须对动梁速度进行跟踪控制[1-2]。300 MN模锻水压机动梁速度控制系统具有巨大惯性、载荷瞬变和控制滞后等特性,这些都将影响水压机动梁速度跟踪控制的响应速度、控制精度和鲁棒性[3]。所以,研究其动梁速度跟踪控制具有非常重要的理论意义和工程意义,可为等温锻压或模拟等温锻压提供技术基础,为同类控制提供参考。目前,解决上述问题的方法主要有前馈PID串级控制和预测控制。采用第1种方法不能取得满意的控制效果,当前大多采用预测控制[4-5]。Richalet等[6-7]阐述了建立模型预测启发控制或称模型算法控制产生的动因、机理及在工业过程中的应用。目前,预测控制主要有动态矩阵控制(DMC)[8]、扩展时域预测自适应控制[9]、扩展时域自适应控制[10]、广义预测控制(GPC)[11]、广义极点配置预测控制[12-13]、连续时域广义预测控制[14]和内模控制(IMC)[15]等。预测函数控制(PFC)是第3代模型预测控制算法,它是由Richalet和Kuntze等[16]在20世纪80 年代提出的,PFC控制把控制输入的结构视为关键问题,可克服其他模型预测控制可能出现规律不明的控制输入问题,同时具有良好的跟踪能力及较强的鲁棒性,在工业过程中得到广泛应用,如在机器人、雷达的目标跟踪、传热设备和反应炉等到工业过程中取得了一定成果。因此,该水压机动梁速度跟踪控制系统采用PFC控制来解决其控制滞后、速度跟踪和鲁棒性问题[4]。
1 动梁速度跟踪控制原理
针对300 MN模锻水压机动梁速度跟踪控制系统的特点,将 PFC控制和 PID控制相结合,采用基于PFC-(PID-H∞)双闭环串级控制策略。其控制原理框图如图1所示。应用PFC控制为监督层,PID-H∞控制为控制层的透明控制结构。控制系统由2个闭环系统组成,内控制环为基于PID-H∞串级控制的凸轮转角控制环,外控制环为基于预测函数控制器的动梁速度跟踪控制环。将内控制环及后续水路系统看作PFC的广义被控对象,将广义被控对象简化为一阶加纯滞后对象,作为PFC的预测模型。这种控制系统综合了PFC 控制、H∞控制及常规PID 控制的优点。其控制原理是:基于PFC控制原理,由给定的动梁速度根据历史数据和预测模型求得凸轮轴目标转角,转角控制采用PID-H∞串级控制以便保证凸轮转角控制的鲁棒性和控制精度[1];通过控制转角来控制水路系统的流量,从而控制水压机的动梁速度。
2 动梁速度预测函数控制器设计
2.1 锻压速度曲线设定
根据生产工艺要求确定1条锻压速度曲线。
2.2 预测函数控制器设计
2.2.1 预测模型
将基于 PID-H∞串级控制器的凸轮轴转角控制回路看作PFC的广义对象,广义对象看作一阶加纯滞后系统。预测控制模型为:
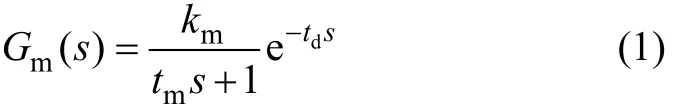
式中:km为增益;tm为时间常数;td为滞后时间常数。km= 0.77,tm=0.7,td= 1.1[17]。
2.2.2 参考轨迹
对于该稳定系统,PFC 控制器参考轨迹采用一阶指数形式,即
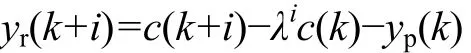
式中:yr为参考轨迹;ts为采样周期;tr为95%的参考轨迹响应时间;c为工艺设定值;yp为系统输出。

图1 基于PFC-(PID-H∞)动梁速度跟踪控制原理图Fig.1 Schematic of speed tracking control for moving beam based on PFC-(PID-H∞)
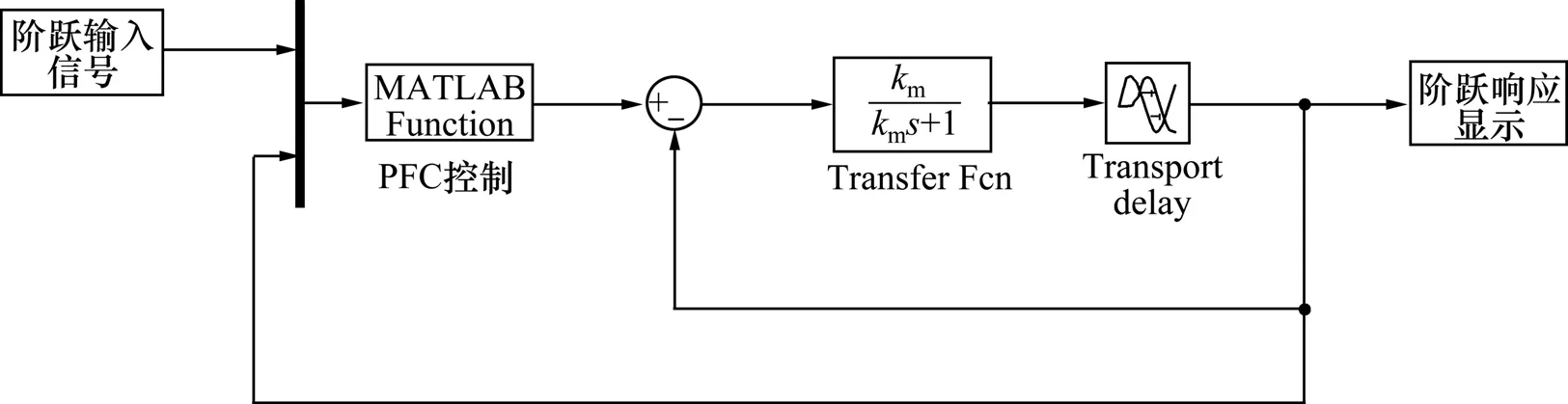
图2 动梁速度PFC动态响应MATLAB仿真模型Fig.2 Simulation model based on MATLAB of PFC dynamic response for moving beam’s speed
3 基于 PFC-(PID-H∞)动梁速度控制仿真
为了解基于PFC-(PID-H∞)双闭环串级动梁速度控制系统的性能,下面从模型失配和外加干扰2个方面进行仿真研究。动态响应 MATLAB仿真模型如图 2所示。
3.1 模型失配
3.1.1 时间常数失配
广义受控对象模型如式(1)所示。当时间常数tm分别为0.3,0.7和0.8时,控制系统动态响应仿真曲线如图3所示。由图3可知:当时间常数增大时,过渡过程时间变长,响应的初始阶段伴有波动,有不稳定趋势;当时间常数减小时,超调量变大,过渡时间变长。

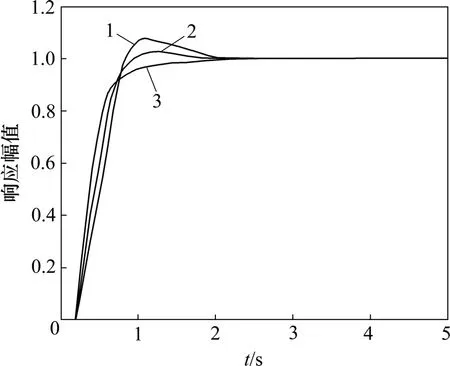
图3 时间常数失配时系统动态响应仿真曲线Fig.3 Dynamic response simulation curve when time constant is mismatched
3.1.2 增益失配
广义受控对象模型如式(1)所示。当增益km分别为0.50,0.77和1.00时,控制系统动态响应仿真曲线如图4所示。可见:当增益失配时,虽然系统保持稳定,但存在较大的余差;当比例系数增大时,过渡过程时间变长;当比例系数减小时,响应加快,超调量增大。
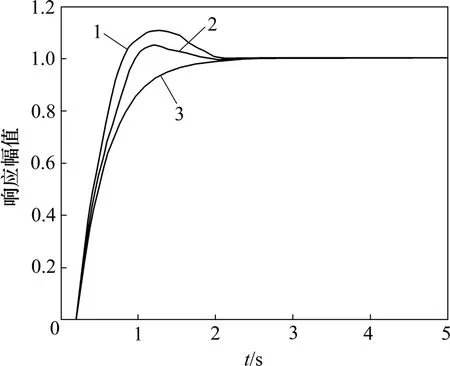
图4 增益失配时系统动态响应仿真曲线Fig.4 Dynamic response simulation curve when gain is mismatched
3.1.3 滞后失配
广义受控对象模型如式(1)所示。当滞后时间常数td分别为0.8,1.1和1.2时,控制系统动态响应仿真曲线如图5所示。由图5可见:因滞后失配,当迟延时间增大时,响应速度变慢,而且在接近稳态时有小的波动;当迟延时间减小时,响应速度加快,但超调量增大,过渡过程时间变长。
3.2 外加干扰
系统在第4 s加入20%负荷阶跃干扰时,控制系统动态响应仿真曲线见图6。由图6可知:基于PFC-H∞双闭环串级控制系统具有很强的外加抗干扰能力,外加干扰基本不会对控制系统品质造成不良影响,能较好地满足工程要求。可见:基于PFC- (PID-H∞)的300 MN模锻水压机速度控制系统在预测模型失配时,控制系统仍具有良好的控制品质,只是在模型失配过大,特别是模型迟延时间失配过大时,系统性能变差;当系统受到外加干扰时,系统具有很强的外加抗干扰能力。所以,PFC 具有较强的抗干扰能力和鲁棒性,具有较大的稳态精度、良好的动态品质和跟踪性能。同时,控制算法简单,对预测模型准确度要求低,易于工程实现,能满足工程要求。
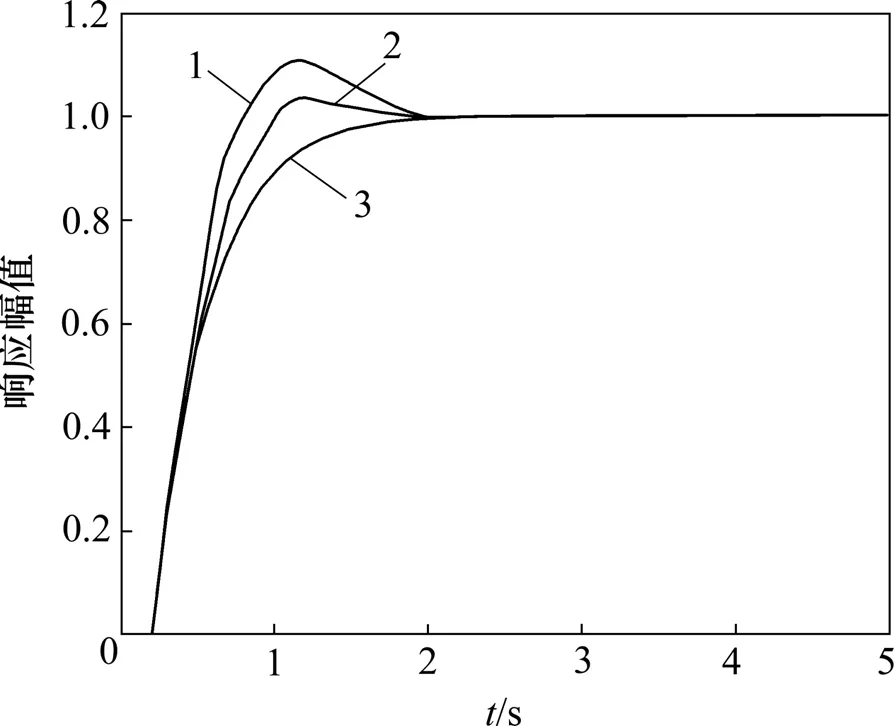
图5 迟延时间常数失配时动态响应仿真曲线Fig.5 Dynamic response simulation curve when lag time constant is mismatched
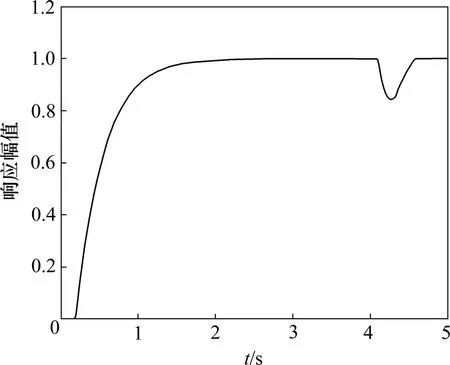
图6 阶跃干扰下系统动态响应仿真曲线Fig.6 Dynamic response simulation curve under disturbance
4 试验
对300 MN模锻水压机动梁速度控制系统,在不同速度、不同工艺条件下,使水压机自动沿着某一速度曲线运行,其中1种工艺条件下的速度实测曲线如图7所示;在一种给定速度曲线条件下,实测动梁速度跟踪曲线如图8所示。
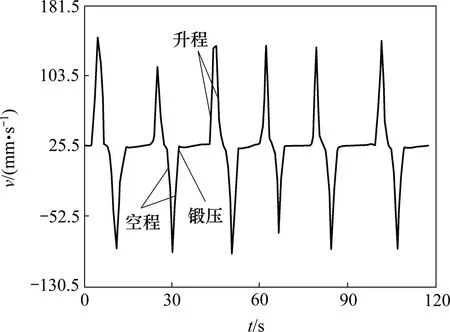
图7 1种工艺条件下实测速度曲线Fig.7 Speed test curve under a process conditions
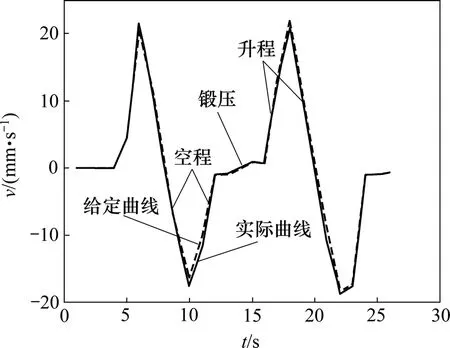
图8 速度跟踪试验曲线Fig.8 Speed tracking test curves
试验结果表明:
(1)在空程、升程和锻压这 3个阶段中锻压阶段动梁速度控制效果最好,重复性最好,空程次之。但在水压机动梁速度控制中,主要对锻压速度的控制要求最高;在空程、升程2个阶段,对速度控制要求较低,所以,能满足生产要求。
(2)在水压机低速锻压阶段比高速锻压阶段的动梁速度控制效果好。这主要是因为低速阶段动梁速度慢,速度容易控制。
(3)水压机锻压速度变化慢阶段比速度变化快阶段的速度控制效果好。这主要是因为水压机控制系统的惯性大,在速度变化快的阶段,锻压速度控制较难。
(4)速度跟踪控制效果良好,在锻压阶段效果优于其他阶段效果,能满足实际要求。
综上所述,动梁速度控制系统的测试结果与仿真结果相互吻合,证实了控制理论、控制模型、控制策略的正确性、可靠性和实用性[17]。
5 结论
(1)基于PFC-(PID-H∞)的300 MN模锻水压机速度控制系统具有较强的抗干扰能力和鲁棒性、较大的稳态精度、良好的动态品质和跟踪性能。
(2)在空程、升程和锻压这 3个阶段中,锻压阶段的动梁速度控制效果最好,重复性最好,空程次之。
(3)在水压机低速锻压阶段比高速锻压阶段的动梁速度控制效果好。水压机锻压速度变化慢阶段比速度变化快阶段的速度控制效果好。在锻压阶段效果的速度跟踪控制效果优于其他阶段的控制效果,能满足实际要求。
(4)仿真结果和试验结果相吻合,证实了研究方法和模型建立的正确性,为同类系统研究提供了参考。
[1] 谭建平, 黄长征, 刘彬, 等. 瞬变载荷下巨型模锻水压机液压操作控制策略研究[J]. 机械工程学报, 2008, 44(11): 272-276.TAN Jian-ping, HUANG Chang-zheng, LIU Bin, et al. Control strategy of hydraulic operation control system under the transient load in giant hydraulic press[J]. Chinese Journal of Mechanical Engineering, 2008, 44(11): 272-276.
[2] 黄长征, 谭建平. 液压机分配阀芯驱动凸轮升程曲线优化设计[J]. 中南大学学报: 自然科学版, 2007, 38(2): 303-308.HUANG Chang-zheng, TAN Jian-ping. Optimization design for cam lifting curve used to drive spool of distributor in hydraulic press[J]. Journal of Central South University: Science and Technology, 2007, 38(2): 303-308.
[3] 黄长征, 谭建平. 300 MN水压机动梁驱动系统锻压速度动态响应特性[J]. 中南大学学报: 自然科学版, 2008, 39(5):1023-1028.HUANG Chang-zheng, TAN Jian-ping. Forging speed’s response characteristic of moving beam drive system for 300 MN die forging hydraulic press[J]. Journal of Central South University: Science and Technology, 2008, 39(5): 1023-1028.
[4] Anwar S. Generalized predictive control of yaw dynamics of a hybrid brake-by-wire equipped vehicle[J]. Mechatronics, 2005,15(9): 1089-1108.
[5] 席裕庚. 预测控制[M]. 北京: 国防工业出版社, 1993: 10-13.XI Yu-geng. Predictive control[M]. Beijing: National Defense Industry Press, 1993: 10-13.
[6] Richalet J, Rault A, Testud J L, et al. Model predictive heuristic control: Application to industrial processes[J]. Automatica, 1978,14(5): 413-428.
[7] Rouhani R, Mehra R. K. Model algorithmic control (MAC),basic theoretical properties[J]. Automatica, 1982,18(4):401-414.
[8] Culter C R, Ramaker B L. Dynamic matrix control: A computer control algorithm[C]//Proc JACC. SanFranciso, 1980: 5-8.
[9] De Keyser R M C, Van Cauwenberghe A R. A self-tuning multistep redictor application[J]. Automatica, 1981, 17(1):167-174.
[10] Ydstie P S. Extended horizon adaptive control[C]//Proceedings of IFAC 9th World Congress. Budapest, Hungary: Pergamon Press Ltd, 1984: 133-137.
[11] Clarke D W, Mohtadi C, Tuffs P S. Generalized predictive control (Part 1): The basic algorithm; Part 2: Extensions and interpretations[J]. Automatica, 1987, 23(2): 137-160.
[12] Lelic M A, Zarrop M B. Generalized pole-placement self-tuning controller (Part 1): Basic algorithm[J]. Intl J Control, 1987, 46(2):547-568.
[13] Lelic M A, Zarrop M B. Generalized pole-placement self-tuning controller[J]. Intl J Control, 1987, 46(2): 569-601.
[14] Demircloglu H, Gawthrop P J. Continuous-time generalized predictive control (CGPC)[J]. Automatica, 1991, 27(1): 55-74.
[15] Garcia C E, Morari M. Internal model control 1. A unifying review and some new results[C]//I&EC Process Des Dev. 1982:308-323.
[16] Kuntze H B, et al. On the predictive functional control of an elastic industrial robot[C]//Proc 25th CDC. Athens, Greece, 1986:1877-1881.
[17] 郑征, 田书. 基于MATLAB的辅助变量法参数辨识与仿真[J].计算机应用与软件, 2004, 21(7): 127-129.ZHENG Zheng, TIAN Shu. Supplementary variable parameter identification and emulate based on MATLAB[J]. Computer Applications and Software, 2004, 21(7): 127-129.
