基于切比雪夫I型低通滤波器设计IIR数字带通滤波器*

陈绍荣 ，刘郁林 ，王 开 ，徐 舜

（1.陆军工程大学 通信士官学校，重庆 400035；2.重庆市经信委，重庆 400015）

0 引 言

在国内外《数字信号处理》著作[1-3]中，均介绍了IIR数字低通滤波器的设计方法。关于IIR数字高通、带通及带阻滤波器的设计，一般有两种方法：一是先在s域上设计相应的模拟高通、带通及带阻滤波器，再通过双线性变换完成IIR数字高通、

数字带通及数字带阻滤波器的设计；二是先在s域上设计相应的模拟低通滤波器，再将模拟低通滤波器变换成IIR数字低通滤波器，最后将IIR数字低通滤波器在相应的变换函数下变换成IIR数字高通、数字带通及数字带阻滤波器，那么研究相应的变换函数就成为关键问题。由于模拟低通、高通、带通和带阻滤波器设计已经有了一套相当成熟的方法，它不但有一套完整的设计公式，而且还有较完整的图表供查询。充分利用这些已有的资源，将会给IIR数字滤波器设计带来很大的方便。基于这一事实，通常采用第一种方法设计IIR数字高通、数字带通及数字带阻滤波器。而所列著作[1-3]中，个别之处的推理过略，不便于理解。本文在文献[4]的基础上，详细阐明了基于切比雪夫I型低通滤波器设计IIR数字带通滤波器涉及的基本原理、过程、步骤及方法。

1 切比雪夫I型低通滤波器设计

1.1 归一化切比雪夫多项式

归一化切比雪夫多项式定义为：

现将计算的结果制成表格，如表1所示。

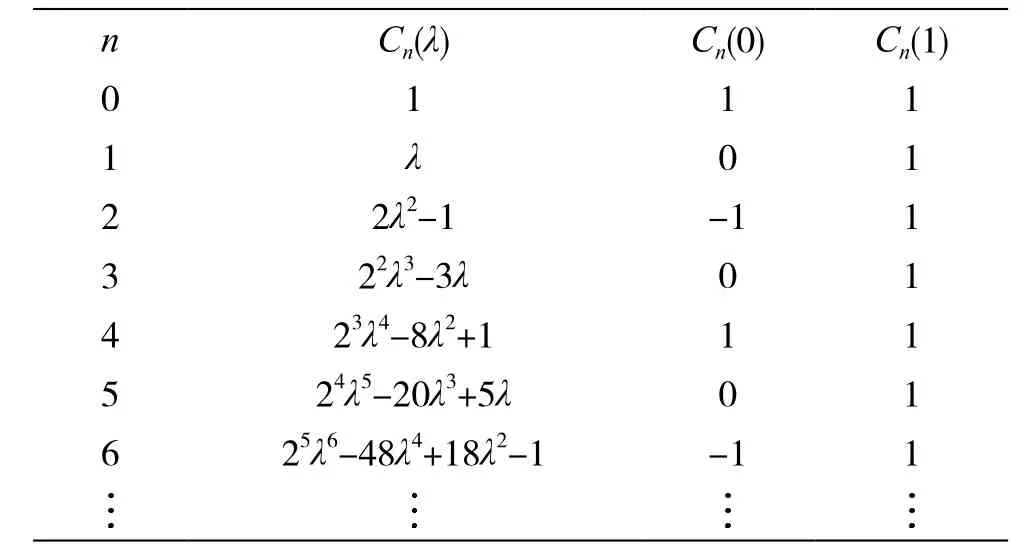
表1 归一化切比雪夫多项式

由表1可知，归一化切比雪夫多项式Cn(λ)是λ 的 n 次多项式，且首项为 2n-1λn。当 |λ|≤ 1 时，Cn(λ)在 -1 至 1 之间 波动 变化， 当 |λ|＞1 时，Cn(λ)按双曲余弦单调递增。

1.2 归一化切比雪夫I型模拟低通滤波器极点分布的特点

归一化切比雪夫I型模拟低通滤波器的幅频特性平方函数定义为：

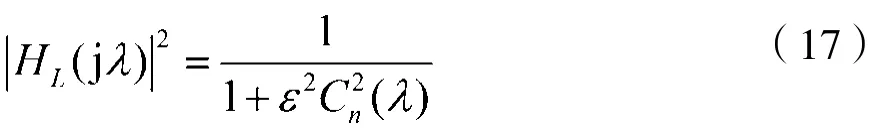
式中，λ=Ω/Ωp为归一化角频率。0＜ε＜1，ε是表示通带内（0≤λ≤1的范围）波纹大小的一个参数，ε越大，波纹越大。n为归一化切比雪夫I型模拟低通滤波器的阶数。在阻带范围（1＜λ≤∞的范围），|HL(jλ)|2是一个单调递减函数。

考虑到式（17），则有：

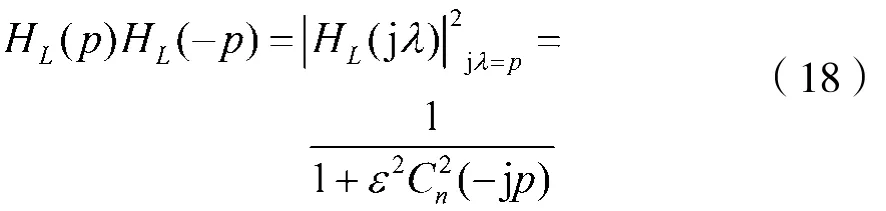
令：

式（19）可写成：

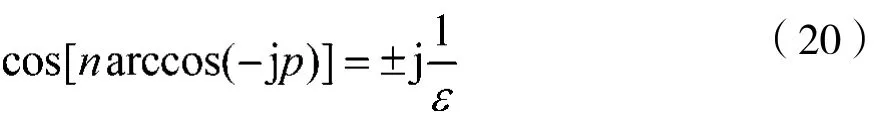
定义φ=arccos(-jp)，则有：

显然，φ应是复数。为此，令φ=φ1+jφ2，则有：

式中，l=1,2,3,…,2n。

如果令 pl=σl+jλl，考虑到式（29），则有：

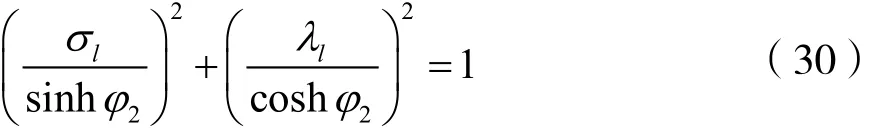
显然 coshφ2＞sinhφ2，因此椭圆的焦点在 p 平面的虚轴上。式（30）表明，归一化切比雪夫I型模拟低通滤波器极点pl的实部和虚部满足椭圆方程，即极点pl落在椭圆上。

由式（29）求出2n个极点pl，一半属于HL(p)，一半属于HL(-p)。为保证所设计的归一化切比雪夫I型模拟低通滤波器是稳定系统，应将p平面左半面的极点赋于HL(p)，规定φ2＞0，l=1,2,3,…,n，那么：

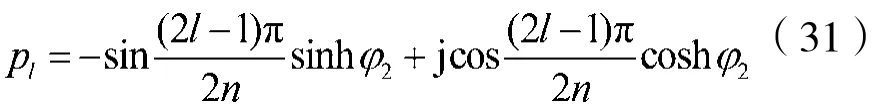
式中，l=1,2,…,n。显然，pl的实部小于0，即这n个极点属于HL(p)。

由于归一化切比雪夫多项式Cn(λ)首项为2n-1λn，考虑到式（16），那么归一化切比雪夫I型模拟低通滤波器的转移函数可表示成：

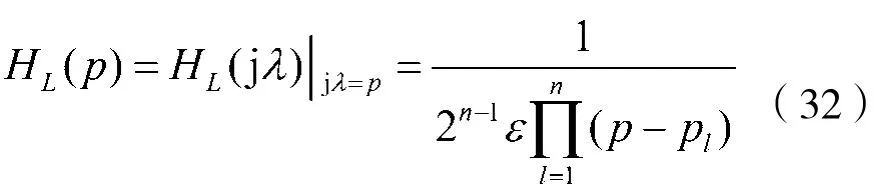
式中，极点pl由式（31）确定。

1.3 切比雪夫I型模拟低通滤波器的设计步骤

（1）将频率作归一化处理，得到归一化切比雪夫I型模拟低通滤波器幅频特性平方函数。

（2）确定归一化切比雪夫I型模拟低通滤波器的波纹参数ε及阶数n。

考虑到式（16），则衰减函数α(λ)可表示成：

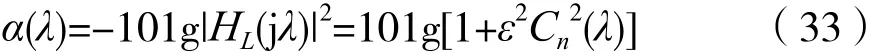
设λ=λp时，通带允许的最大衰减为αp，考虑到式（33），则有：设λ=λs时，阻带应达到的最小衰减为αs，考虑到式（33），则有：

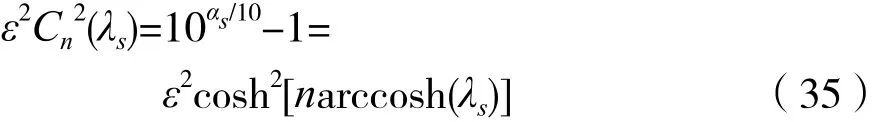
考虑到 λ=Ω/Ωp，则有 λp=Ωp/Ωp=1，由表 1 可知(λp)=(1)=1，那么式（34）可写成：

考虑到式（36），由式（35）可得：

这样，首先利用式（36）可求出波纹参数ε；再利用式（37）计算出a2值，最后利用式（38）就可以求出归一化的切比雪夫I型滤波器的阶数n。

（3）利用式（28）、式（31）及式（32），可求出归一化切比雪夫I型模拟低通滤波器的转移函数HL(p)。

（4）作逆归一化处理，令p=s/Ωp，可从归一化的切比雪夫I型模拟低通滤波器的转移函数HL(p)得到切比雪夫I型模拟低通滤波器的转移函数H(s)，即：

2 模拟带滤波器的设计

可以通过频率变换的方法，借助巴特沃斯模拟低通滤波器或切比雪夫I型模拟低通滤波器来完成模拟带通滤波器的设计，其设计过程，如图1所示。

图1 模拟带通滤波器的设计过程

2.1 模拟带通滤波器到模拟低通滤波器的频率变换公式

模拟带通滤波器的四个频率参数是Ωsl、Ω1、Ω3和Ωsh。Ω1、Ω3分别是通带的下截止频率和上截止频率；Ωsl是下阻带的上截止频率，Ωsh是上阻带的下截止频率。

为了作频率的归一化处理，定义ΩBW=Ω3-Ω1为通带宽度，以此作为参考频率，对带通滤波器的四个频率作归一化处理，即：

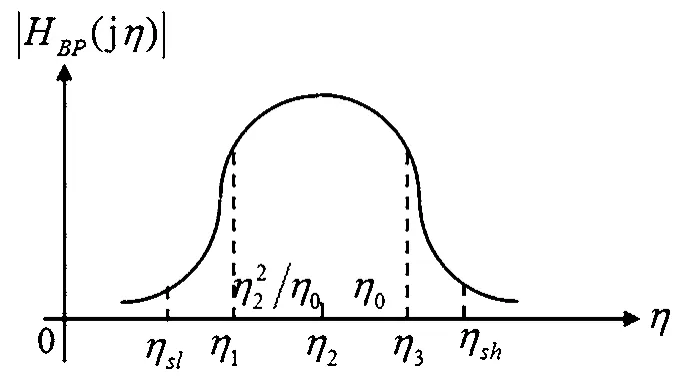
图2 归一化模拟带通滤波器的幅频特性

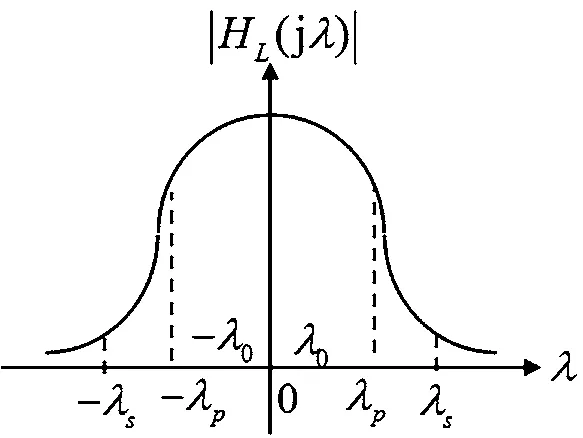
图3 归一化低通滤波器的幅频特性

为了保证频率变换后，两个归一化的幅频特性|HBP(jη)|和|HL(jλ)|，在通带内和阻带内的衰减数相同，各频率点的对应关系，如表2所示。

为了找出对应的关系式， 设η2＜η0＜η3，0＜λ0＜λp，现让 η 轴上的点 η0对应 λ轴上的点 λ0。考虑到η3=η22/η1，那么点 η0在 η 轴上的对应点为η22/η0。 因 为 η2＜η0＜η3， 所以η22＜η0η2＜η2/η3， 即η22＜η0η2＜η23/η1，那么有 η1＜η22/η0＜η2，即点 η0在 η 轴上的对应点η22/η0位于η轴上点η1与η2之间。考虑到0＜λ0＜λp，则-λp＜-λ0＜0，即λ轴上点λ0的对应点-λ0位于λ轴上的点-λp与0之间。

表2 归一化模拟带通及低通滤波器幅频特性各频率点的对应关系

为了保证频率变换后，两个归一化的幅频特性|HBP(jη)|和|HL(jλ)|，在通带内和阻带内的衰减dB数相同，那么各频率点相对于对称轴的压缩比应该相同，即：

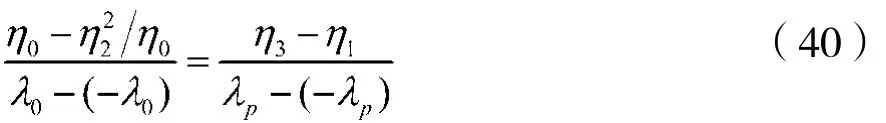
考虑到 η3-η1=1，λp=1，将 λ0及 η0分别用 λ及η代替，那么由式（40）可得出归一化频率λ与η满足下述关系：

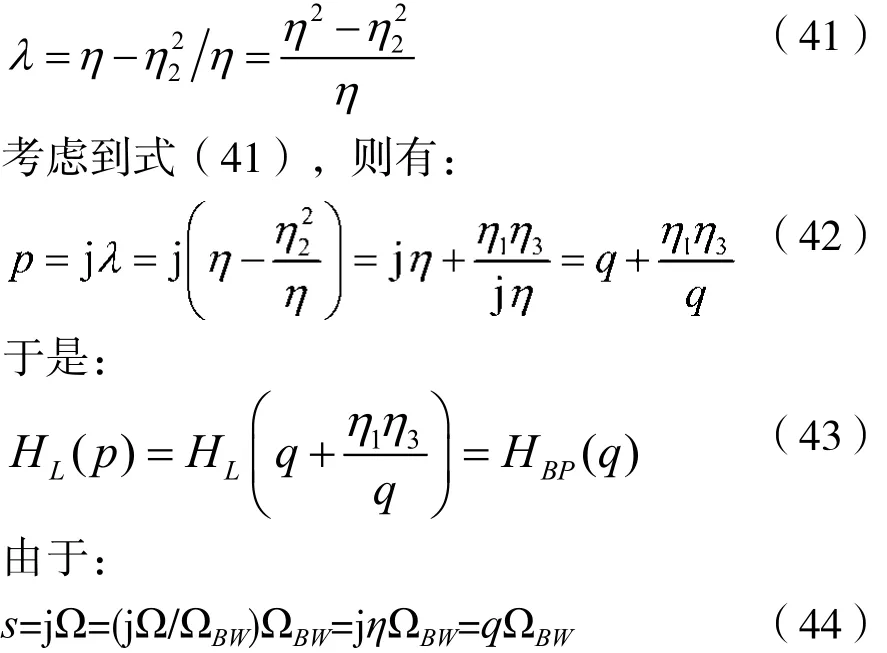
考虑到式（44）及式（43），则可得模拟带通滤波器的转移函数，即：

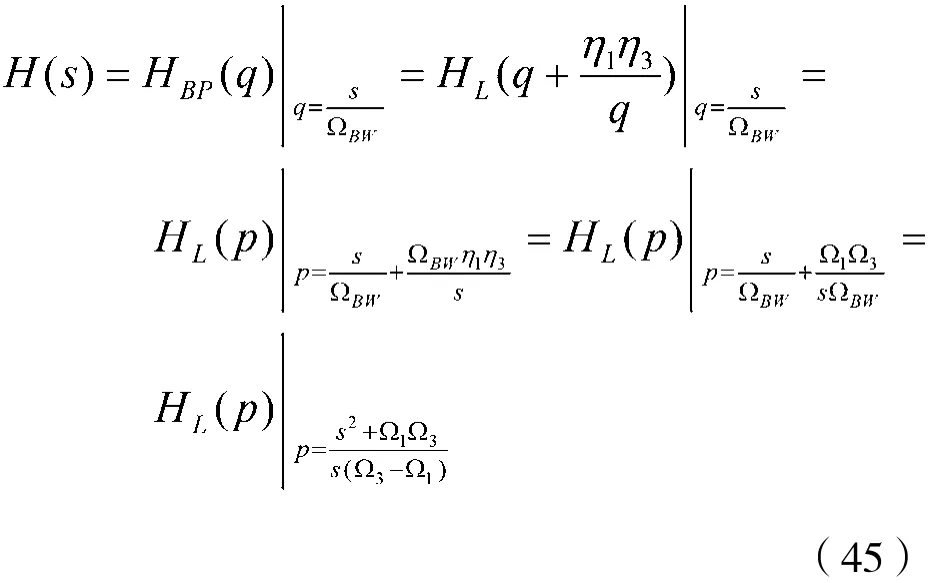
可见，n阶模拟低通滤波器转换成模拟带通滤波器后，其阶次变为2n。

2.2 利用模拟低通滤波器设计模拟带通滤波器的步骤

（1）将模拟带通滤波器的四个实际频率归一化处理，获得：

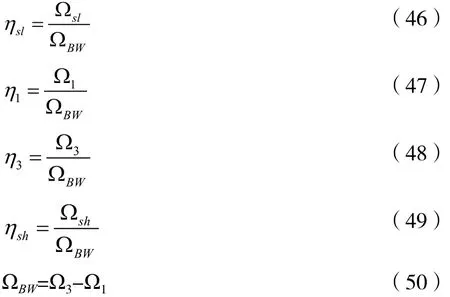
（2）利用式（41）作频率变换，并考虑到频率点的对应关系，则有：

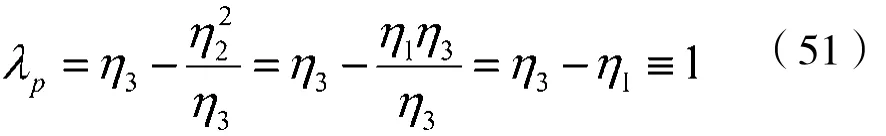
因此，λp=1可直接给出，而αp、αs保持不变。其中，αp、αs分别为待设计的模拟带通滤波器通带允许的最大衰减及阻带应达到的最小衰减。

（3）按要求设计模拟低通滤波器，得到HL(p)。

（4）利用式（45）得到模拟带通滤波器的转移函数H(s)。

3 双线性变换

3.1 双线性变换函数

双线性变换函数定义为：

式（55）揭示了s平面与z平面的单值映射关系，即“一对一”映射关系，将这种映射变换关系称为双线性变换。

3.2 模拟角频率Ω与数字角频率ω之间的关系

考虑到式（55），则有：

利用冲激响应不变法设计IIR数字带通滤波器时，模拟角频率Ω与数字角频率ω之间是线性关系，即Ω=ω/T，其中T为抽样间隔。而式（57）表明，模拟角频率Ω与数字角频率ω之间产生了畸变，不再保持线性关系，而是非线性的正切函数关系。

4 数字带通滤波器的设计

关于数字带通滤波器的设计，这里采用的方法是首先在s域上设计相应的模拟带通滤波器，再通过双线性变换来完成z域上数字带通滤波器的设计。

4.1 用双线性变换法设计IIR数字带通滤波器的过程

利用双线性变换法设计IIR数字带通滤波器的过程，如图4所示。

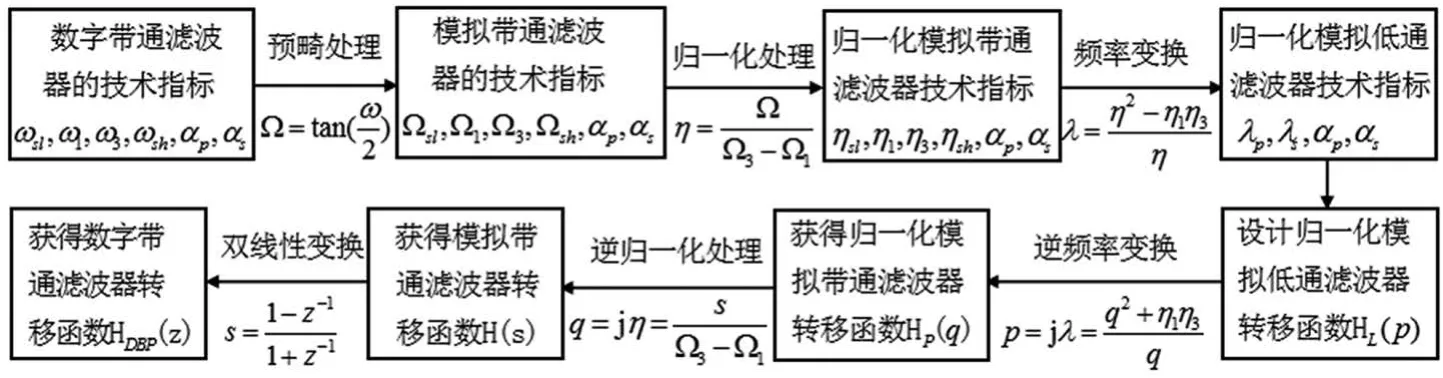
图4 用双线性变换法设计IIR数字带通滤波器的过程

4.2 用双线性变换法设计IIR数字带通滤波器的步骤

由图4可知，用双线性变换法设计IIR数字带通滤波器时，将经历下述步骤。

4.2.1 作预畸处理

将给定的数字带通滤波器的技术指标ωsl、ω1、ω3、ωsh、αp及 αs变换成模拟带通滤波器的技术指标：

此外，αp及αs保持不变。

4.2.2 作归一化处理

将模拟带通滤波器的技术指标Ωsl、Ω1、Ω3、Ωsh、αp及αs变换成归一化模拟带通滤波器的技术指标，若定义ΩBW=Ω3-Ω1，则有：

4.2.3 作频率变换

将归一化模拟带通滤波器的技术指标ηsl、η1、η3、ηsh、αp及αs变换成归一化模拟低通滤波器的技术指标，利用式（41）作频率变换，并考虑到频率点的对应关系有：

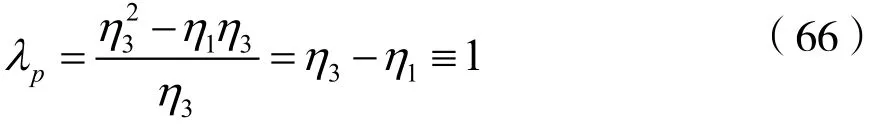
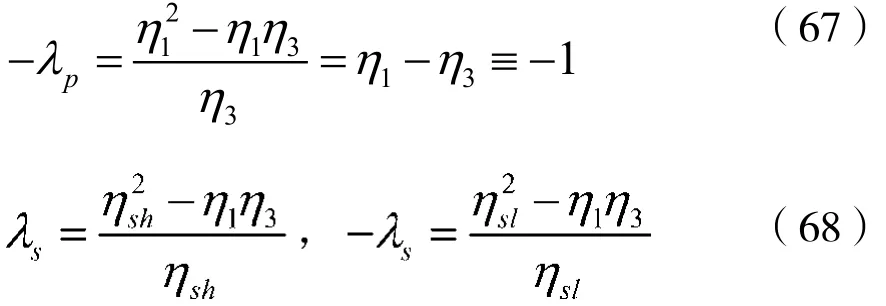
此外，αp及αs保持不变。

4.2.4 设计归一化模拟低通滤波器

依据归一化模拟低通滤波器的技术指标λp=1、λs=min[|λs|,|-λs|]、αp及 αs，可以选用巴特沃斯模拟低通滤波器或切比雪夫Ⅰ型模拟低通滤波器进行设计，得到归一化模拟低通滤波器的转移函数HL(p)。

4.2.5 作逆频率变换

通过式（42）作逆频率变换，可以获得归一化模拟带通滤波器的转移函数HBP(q)，即：

4.2.6 作逆归一化处理

通过式（44）作逆归一化处理，可以获得模拟带通滤波器的转移函数H(s)，即：

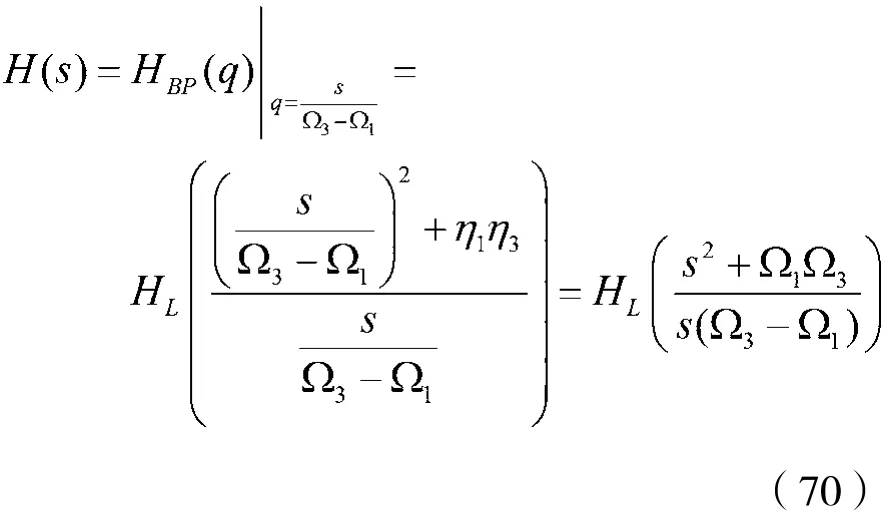
4.2.7 作双线性变换

通过式（55）作双线性变换，可以获得IIR数字带通滤波器的转移函数HDBP(z)，即：

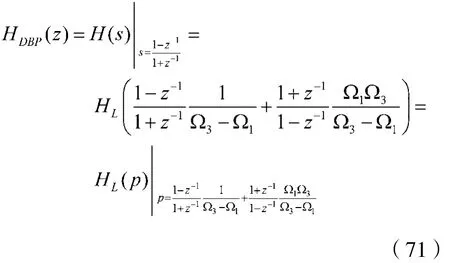
从式（71）知道，可将后面三个步骤合为一步，便可完成IIR数字带通滤波器的设计。

4.3 IIR数字带通滤波器的设计举例

例4.1：试用切比雪夫I型模拟低通滤波器设计一个数字带通滤波器。技术指标要求：通带范围为200～400 Hz，通带最大衰减，101g(4/3)dB在100 Hz以下和500 Hz以上衰减不小于18 dB，抽样频率fs=1 200 Hz。

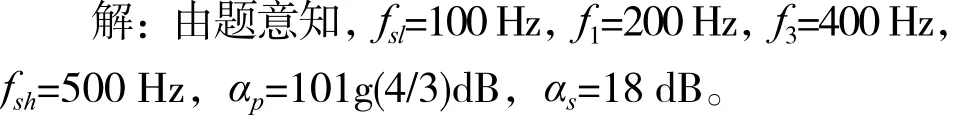
（1）将数字带通滤波器的频率参数变换成归一化的数字角频率参数

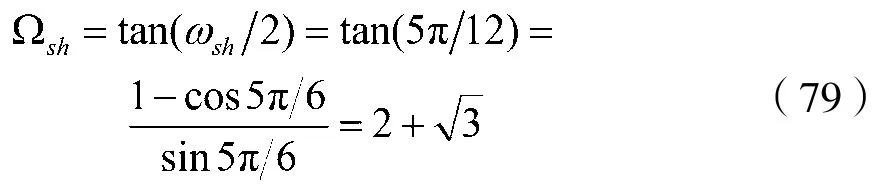
（3）将模拟带通滤波器的频率作归一化处理若定义ΩBW=Ω3-Ω1，则有：

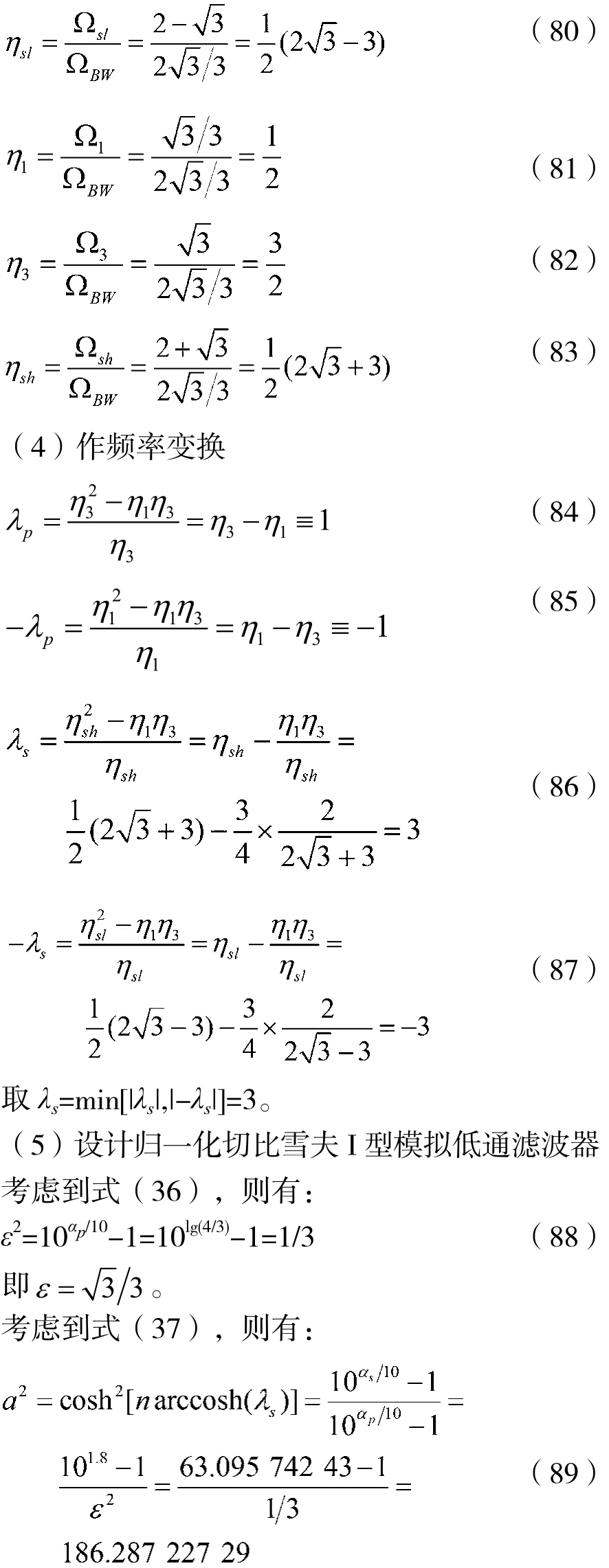
于是a=13.648 707 898 2。

考虑到式（32），则有：

（6）作逆频率变换

由式（69），并考虑到式（109），可得：

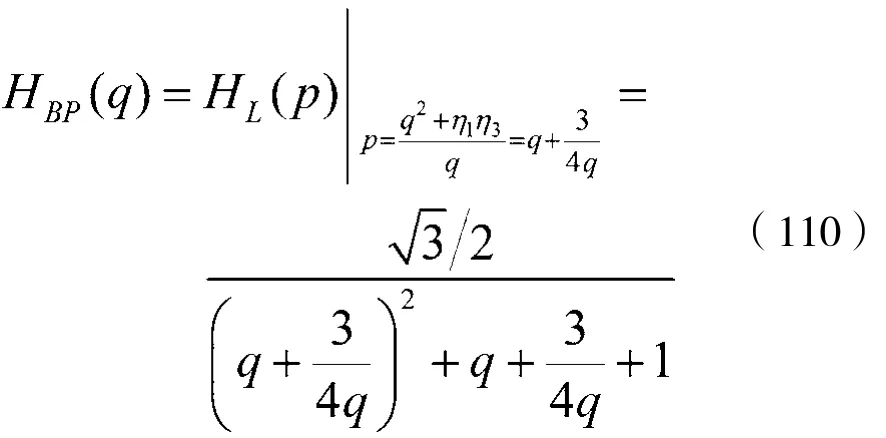
（7）作逆归一化处理

由式（70），并考虑到式（110），可得：

由式（55），并考虑到式（111），可得：

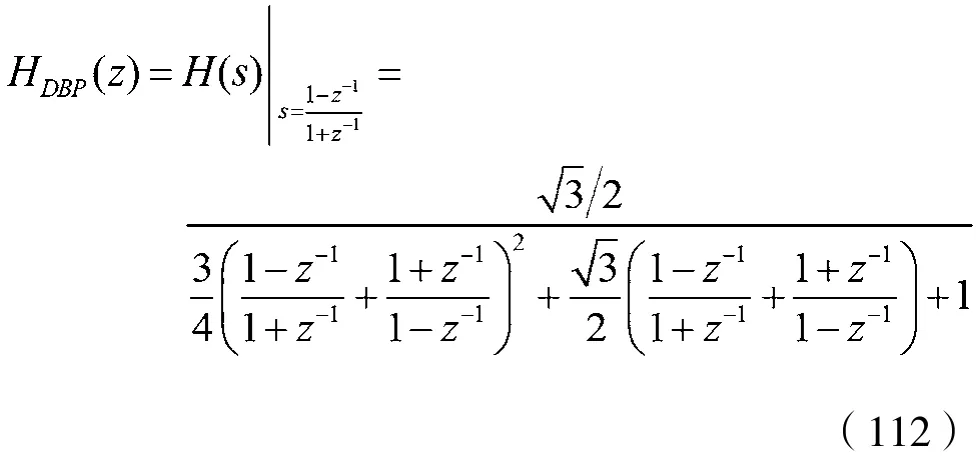
下面检验设计的数字带通滤波器是否满足各项指标要求

考虑到式（112），则数字带通滤波器的频率特性为：

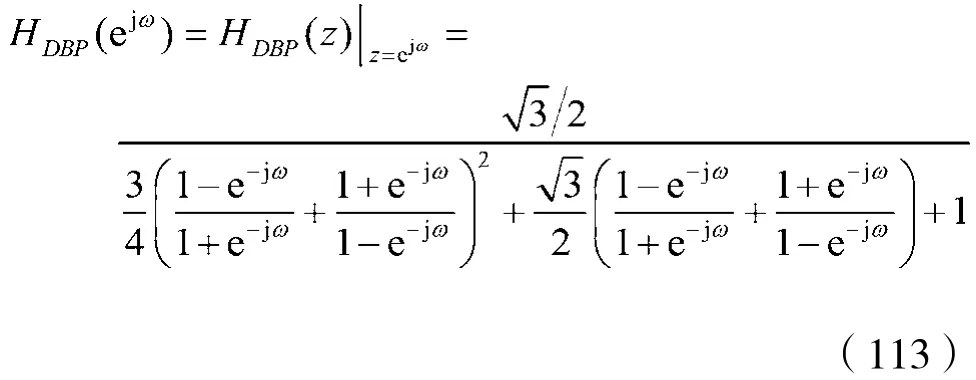
于是：

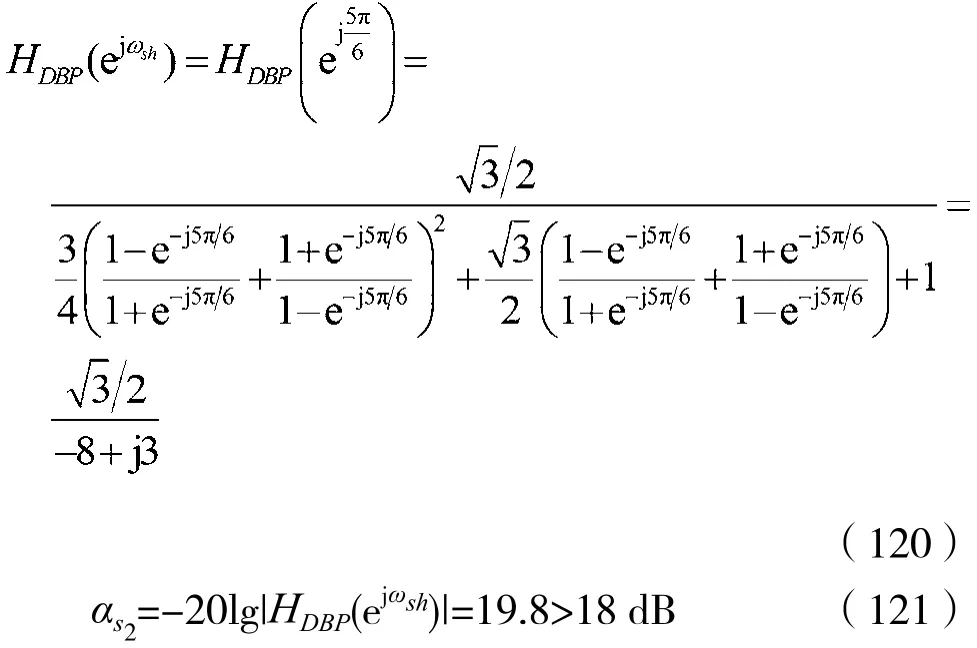
因此，所设计的数字带通滤波器满足技术指标要求。

5 结 语

本文介绍了归一化切比雪夫多项式、归一化切比雪夫I型模拟低通滤波器极点分布的特点、归一化切比雪夫I型模拟低通滤波器的设计步骤，阐述了模拟带通滤波器到模拟低通滤波器的频率变换公式及利用模拟低通滤波器设计模拟带通滤波器的步骤。最后，介绍了利用双线性变换法设计IIR数字带通滤波器的步骤，并给出了基于切比雪夫I型低通滤波器来设计IIR数字带通滤波器的实例。