基于SWT的电力系统基波检测
2022-09-28陶佳兰陈贵词
陶佳兰,喻 敏,陈贵词,王 斌
基于SWT的电力系统基波检测
陶佳兰1,2,喻 敏1,2,陈贵词1,2,王 斌3
(1.冶金工业过程系统科学湖北省重点实验室(武汉科技大学),湖北 武汉 430065;2.武汉科技大学理学院,湖北 武汉 430065;3.武汉科技大学信息科学与工程学院,湖北 武汉 430081)
在噪声混入含有基波的信号时,传统的时频分析方法在基波提取过程中易出现模态混叠。为了准确检测出基波分量,利用时频分析精度较高的同步挤压小波变换(Synchrosqueezing Wavelet Transform, SWT)实现基波检测。首先,采用SWT将含有基波的信号分解为一组内蕴模态类函数(Intrinsic Mode Type functions, IMTs),第一个分量IMT1即代表基波。然后,该分量经Hilbert变换实现基波频率和幅值的测量。在谐波幅值瞬变、噪声混入、基波频率波动、间谐波频率靠近基波和谐波的情境下进行算法验证。实验结果表明,SWT能够准确提取基波,频率精度最高可达10-8量级,具有较强的抗噪性,且SWT的基波提取能力强于谐波和间谐波。
基波检测;模态混叠;同步挤压小波变换;希尔伯特变换;抗噪性
0 引言
在电力系统故障诊断、仪器仪表输出信号的处理、电能质量分析等领域[1],需要从含有噪声的信号中提取基波信息,且各种电力设备在电力系统非线性负荷和电力系统电压作用下,易发生扰动[2],并伴随大量影响电能质量的谐波和间谐波,而部分谐波和间谐波检测的相关研究,也需依赖于所提取到的高精度基波频率[3]。所以,准确地从电力系统信号中检测出基波参数对电力系统的稳定运行具有重要的工程实用价值,同时也是部分谐波和间谐波检测研究工作的基础[4]。
目前,时频分析方法在基波检测中较为常见,但不同的时频分析方法因电力系统环境的不同,基波检测效果各有优劣。快速傅里叶变换(Fast Fourier Transform, FFT)[5]适用于平稳周期电力信号的基波提取,且要求满足采样同步,否则容易出现频谱泄露和栅栏效应[6]。而短时傅里叶变换(Short Time Fourier Transform, STFT)分析窗的长度固定,对于含有基波的暂态扰动,不易在时域和频域同时达到较高的精度检测要求,且计算量稍大[7]。小波变换(Wavelet Transform, WT)[8]的基波检测效果则取决于最优小波基本函数的选取[9]。相比传统窗函数固定的STFT与基函数固定的WT,希尔伯特-黄变换(Hilbert-Huang Transform, HHT)[10]包含经验模态分解(Empirical Mode Decomposition, EMD)和Hilbert变换两部分,因EMD中的基函数具有自适应性,所以更适用于非平稳信号,经EMD可得到代表基波和谐波等不同频率分量的固有模态函数(Intrinsic Mode Functions, IMFs),但EMD存在的模态混叠问题[11]会影响电力系统信号分解的精度,继而产生EMD的系列改进方法:集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)[12]和自适应噪声的完全集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN)[13]等,但EEMD可能使原信号被噪声污染,计算量大,CEEMDAN计算量虽有减小,却和EEMD一样可能存在虚假分量[14]。而变分模态分解(Variational Mode Decomposition, VMD)[15]则是将信号分解问题转化为变分问题,通过迭代搜索变分模型中的最优解,确定出各模态分量的频率中心和最优带宽,但因预先设定模态数目的差异,存在模态过分解和丢失的情况[16]。同步挤压小波变换[17]是由Daubechies等人提出的一种以小波变换为基础的时频重排算法,该方法在时间-尺度上对信号能量进行重新分配,经同步挤压锐化频率曲线,可重构出各频率曲线所对应分量的波形,具有抗噪性,且能有效改善模态混叠问题[18]。
SWT方法已经应用在信号消噪、机械故障诊断等诸多领域。文献[19]将SWT应用于解决风电汇集地区存在的非同步振荡问题,对比FFT和HHT,SWT更为准确地检测出了频率相近的间谐波成分。文献[20]将SWT用于旋转机械振动信号特征提取,有效避免了模态混叠,能够精确描述谐波信号的频率构成。文献[21]首先运用EMD方法分解得到含有模态混叠的IMF3分量,再运用SWT对IMF3分量继续进行分解,得到了与直接使用SWT分解原始信号相一致的分解结果,成功提取出谐波分量。
针对模态混叠使基波提取难度加大的问题,本文在电力系统电压存在谐波幅值瞬变、噪声混入、基波频率波动、间谐波频率靠近基波和谐波的情形下,结合SWT和Hilbert变换实现基波频率和幅值的测量。实验对比EMD、CEEMDAN、VMD与SWT的基波检测效果,分析验证SWT的模态分解能力、抗噪性能以及在基波检测中的准确性。
1 基于同步挤压小波变换的基波提取原理
1.1 同步挤压小波变换原理
同步挤压小波变换通过对所划分的频率区间同步挤压来锐化频率曲线,依据信号在时间-尺度中的能量大小逐步分解出代表基波和谐波等不同频率分量的内蕴模态类函数(Intrinsic Mode Type functions, IMTs)。经同步挤压的各IMT之间不存在交叉项,在模态混叠时也能准确提取基波等不同频率分量。
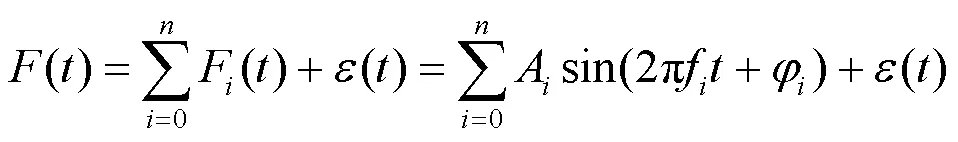
SWT的基波提取主要包括以下5个步骤。
1) 对混有噪声的多分量电力信号进行连续小波变换(Continuous Wavelet Transform, CWT)。

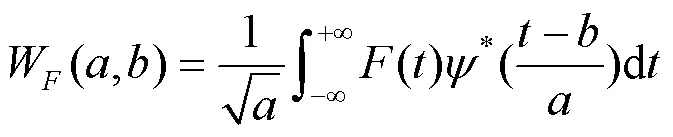
对式(2)进行傅里叶变换,得到连续小波变换系数在频域上的计算公式为
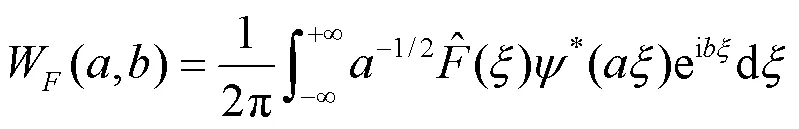
bump小波基函数在频域上可表示为
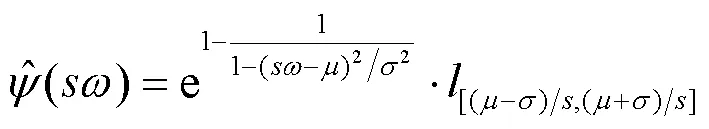
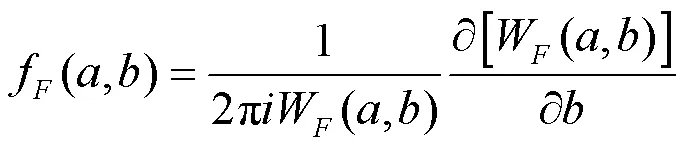
3) 划分信号频率区间。
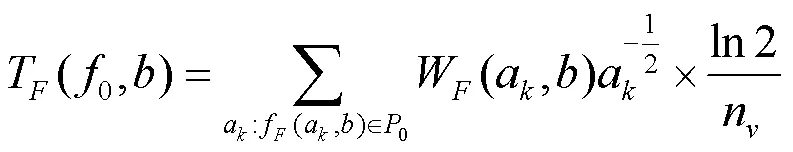
5) 基波分量重构。
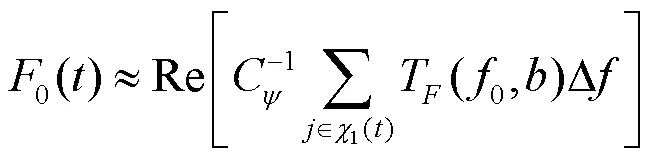
1.2 Hilbert变换原理
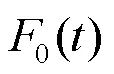
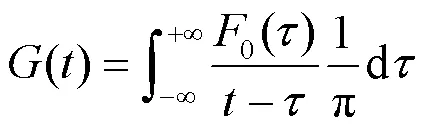
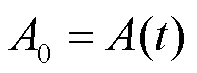
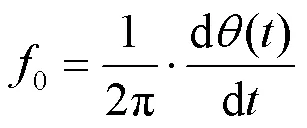
经1.1节同步挤压小波变换的5个步骤,即可完成基波分量的提取,再结合1.2节的Hilbert变换,则能计算出基波分量的特征频率和特征幅值。
基于SWT的基波检测流程如图1所示。
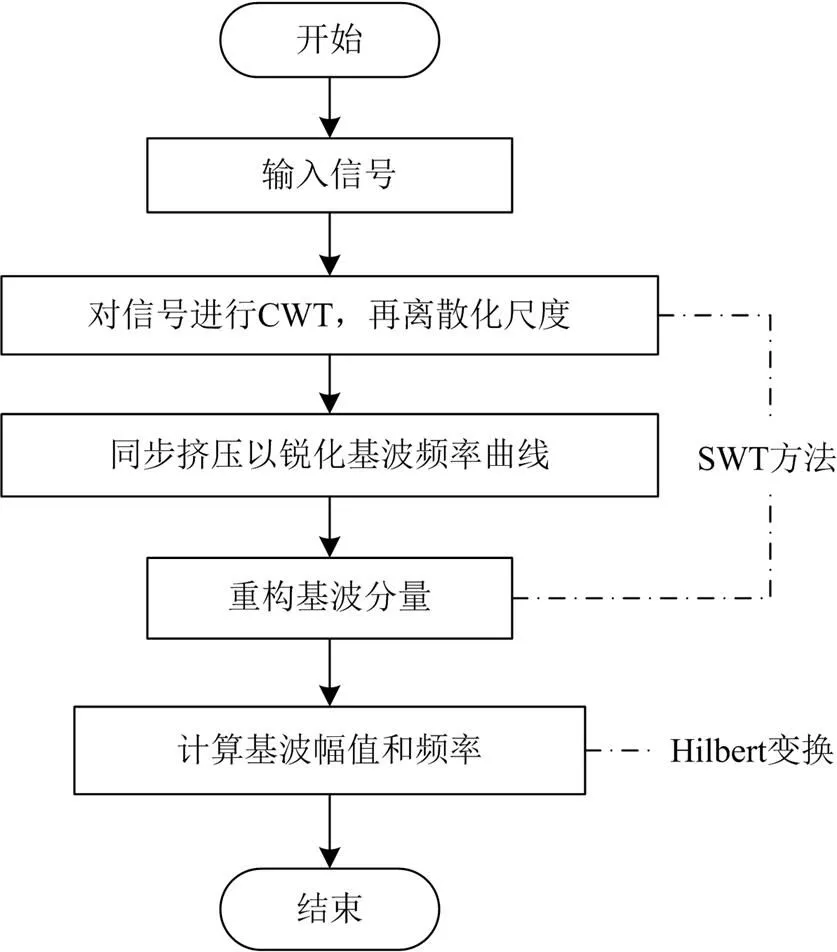
图1 基于SWT的基波检测流程图
2 信号仿真实验与分析
为了验证SWT方法用于基波检测的性能,本文在谐波幅值瞬变、噪声混入、基波频率波动、间谐波频率靠近基波和谐波的情境下分别对暂态电压信号[24-25]开展仿真实验与分析。
2.1 谐波幅值瞬变的仿真信号
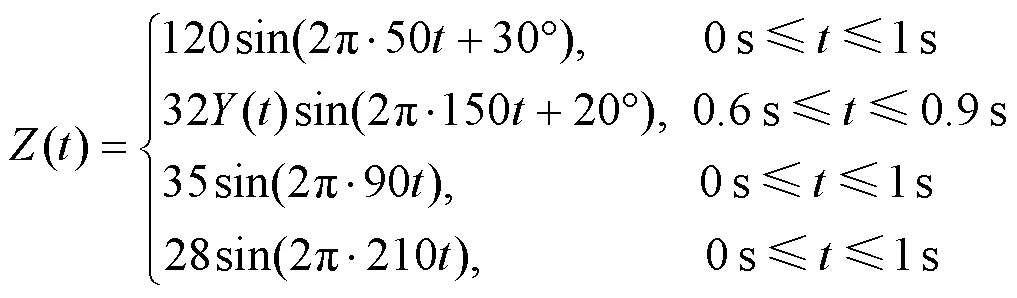
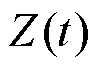
图2 SWT时频分析
将SWT的分解结果与EMD、CEEMDAN、VMD的分解结果对比,其前4项模态分量波形如图3所示。4种方法检测出在后6个周期(图3中箭头所截取的周期数)的基波分量与原始基波的波形吻合效果,如图4所示。
由图3可知,EMD、CEEMDAN、VMD、SWT分解得到的IMF2、IMF3、IMF1、IMT1分量分别对应基波;CEEMDAN的基波提取效果较EMD稍差,波形相比之下略不整齐,两者都出现了模态混叠现象,导致不能从信号()中完全提取出基波;而VMD虽能较为完整地提取出基波,但相比SWT方法的分解结果,VMD存在边界效应,两端峰值较小,且波形不整齐。由此可知,SWT具有更好的模态分解能力,且因SWT检测出后3个IMT模态分量的频率依次为89.999 999 Hz、149.718 474 Hz和210.000 000 Hz,表明其也适用于谐波和间谐波检测。

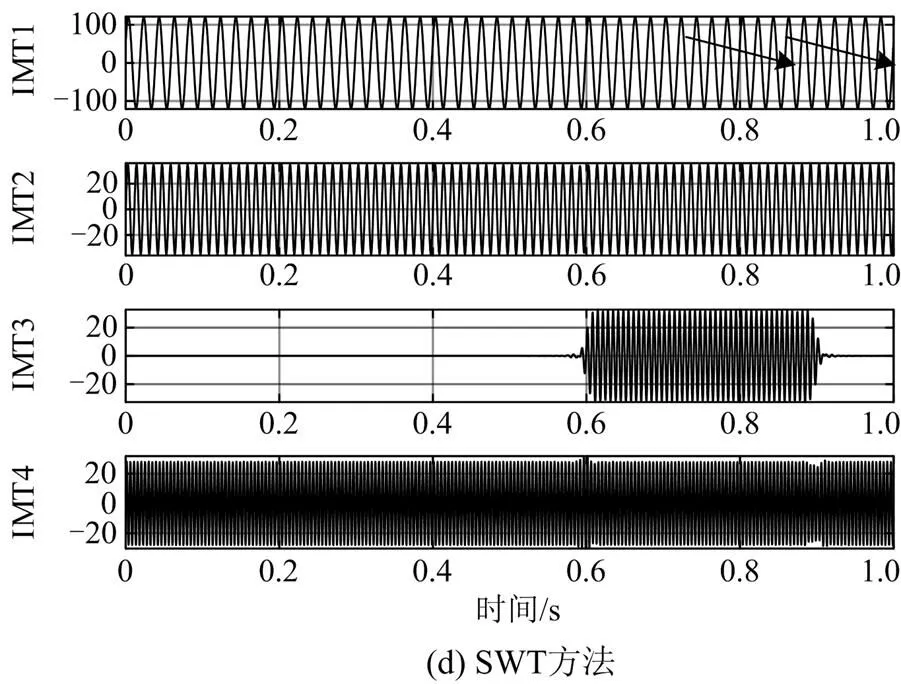
图3 模态分解结果
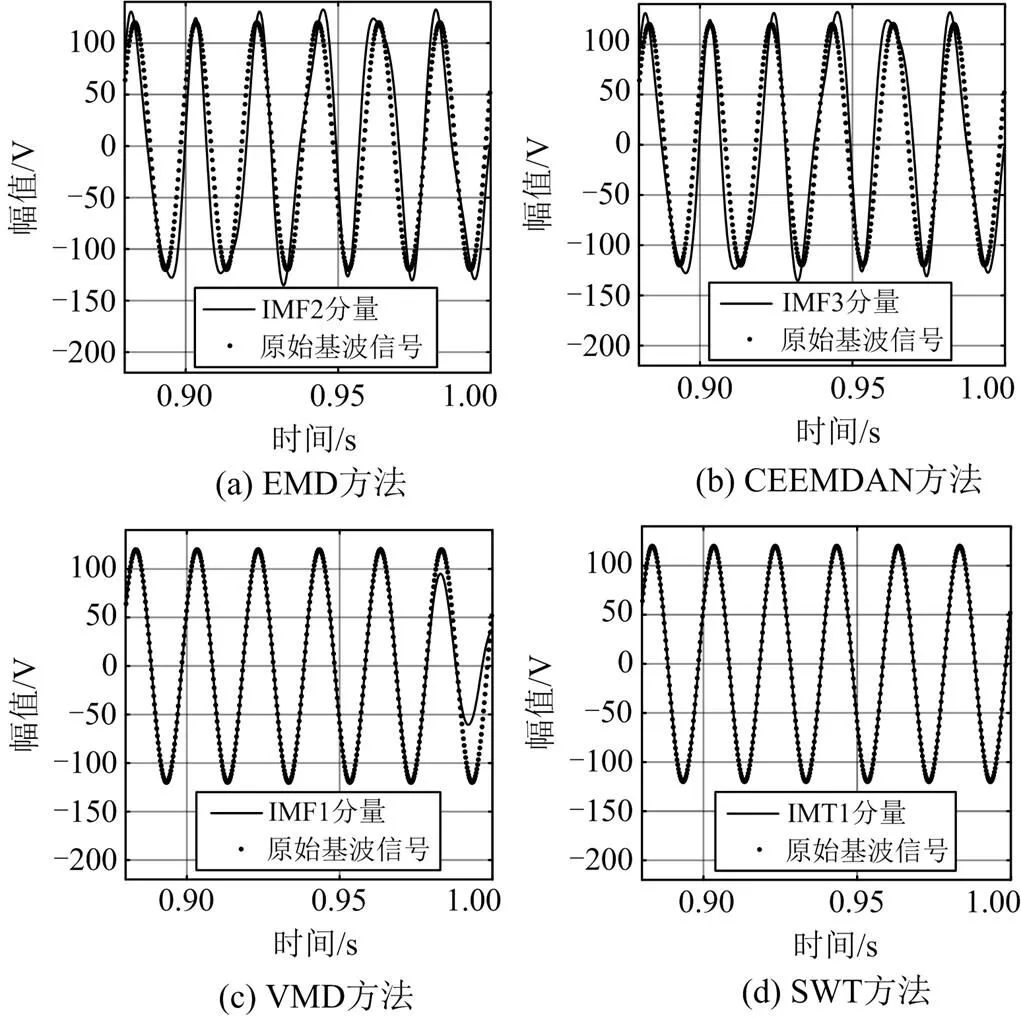
图4 基波波形吻合效果1
由图4可知,因3次谐波的幅值在0.6 s和0.9 s时刻发生阶跃变化, CEEMDAN和EMD的分解结果受到一定程度影响,频率和幅值不稳定,波形不整齐,它们在峰值处的波形与原始基波波形的吻合效果较差;而SWT和VMD在峰值处的整体吻合度较好,但对比之下,SWT在波形右端点处与原始基波波形的吻合效果更好,VMD在最后2个峰值处的幅值明显小于基波幅值,与基波波形的吻合效果略差,由此可知,4种方法的基波波形吻合度排序为SWT>VMD>EMD>CEEMDAN。
为分析4种方法测量出的频率和幅值随时间变化的数值波动稳定性,列出了4种方法经Hilbert变换得到的基波频率、幅值及其标准差的具体数值,如表1所示,其与原始基波频率标准值(50 Hz)和幅值标准值(120 V)之间所存在的相对误差如表2所示。
由表1和表2可以看出,SWT结合Hilbert变换计算得到的基波频率和幅值随时间波动的标准差最小,分别为0.0464和0.2755;对比4种方法检测出的基波频率和幅值所存在的相对误差,精度由高到低排序为SWT>VMD>EMD>CEEMDAN;其中,SWT的基波频率检测精度达到了10-8量级,相比EMD、CEEMDAN和VMD,SWT的检测精度更高,幅值检测精度也达到了10-4量级,同时,对比数字万用表FLUKE15B的技术指标对基波测量参数的最大允许误差(±1.0%)[28],SWT满足该精度要求,表明该方法能够较为准确地实现基波检测,且具有较强的频率测量能力。
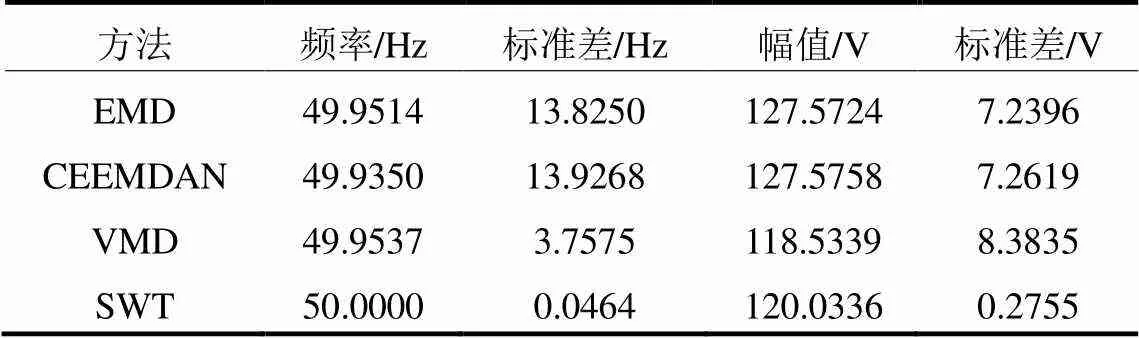
表1 4种方法的检测结果
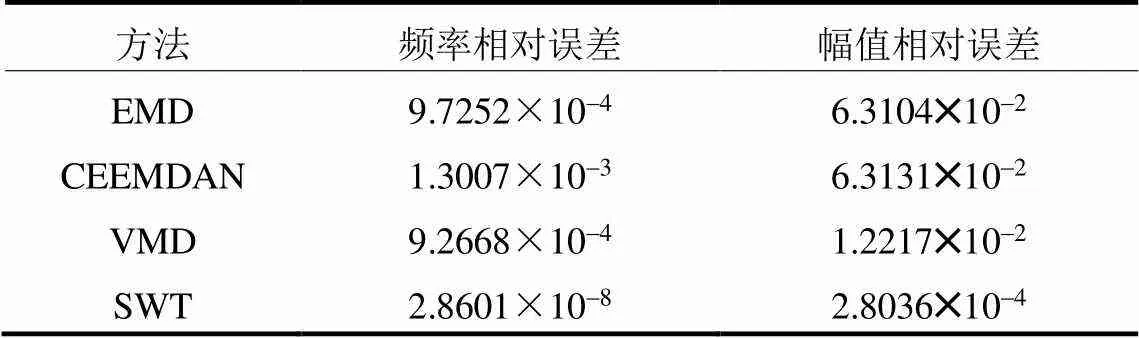
表2 4种方法的基波检测相对误差
由图5可以看出,当NR=20 dB时,因噪声混入,3次谐波的频率曲线波动加剧,210 Hz的频率分量受此影响很大,其频率曲线出现波动和间断的情况,但基波的频率曲线未受明显影响,表明SWT在噪声混入时仍能够检测出基波,具有抗噪性。对比SWT与EMD、CEEMDAN、VMD所分解的不同项模态分量波形,分析比较4种方法抗噪的能力,4种方法的模态波形如图6所示。
由图6可知,噪声混入后,EMD和CEEMDAN的虚假分量变多,代表基波的IMF分量延后出现,它们的 IMF4对应基波分量,但存在严重的模态混叠,不能完全提取出基波;而VMD分解出的IMF1分量即对应基波,但相比SWT分解出的基波IMT1,VMD的整体波形不整齐,存在一定程度的模态混叠,且图6(c)中后3个IMF分量的部分频率和幅值信息也已经被噪声淹没;而SWT不仅能较为完整地提取出基波,且其后3个IMT分量的频率分别为90.000 022 Hz、149.708 364 Hz和209.999 452 Hz,表明在噪声混入时,该方法对谐波、间谐波也具有识别能力,突出了SWT较好的抗噪能力。
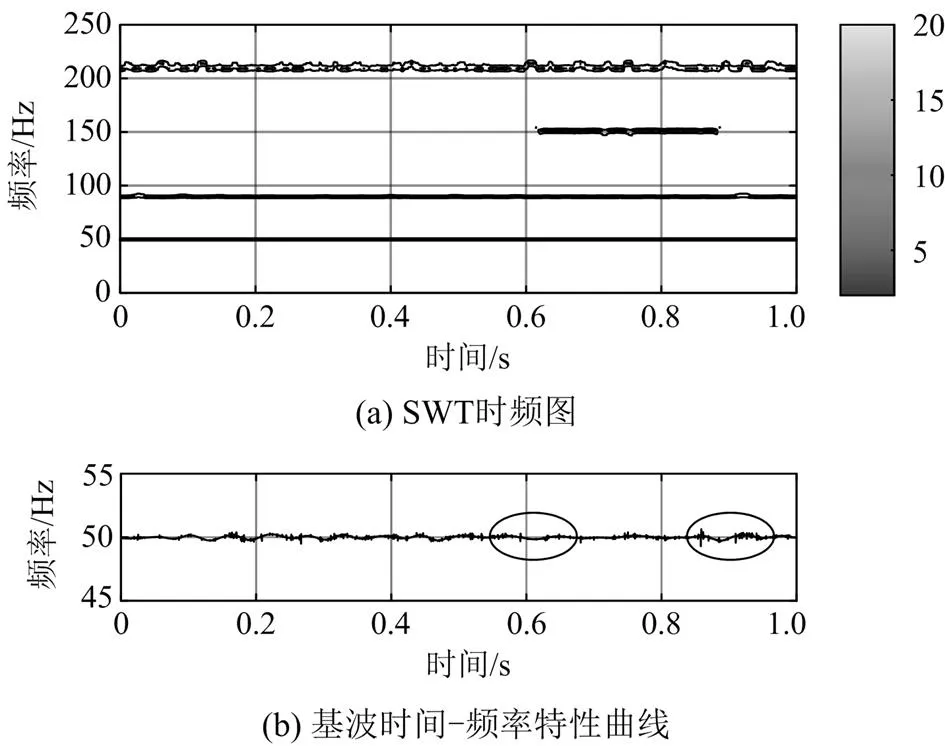
图5 SWT时频分析(SNR=20 dB)

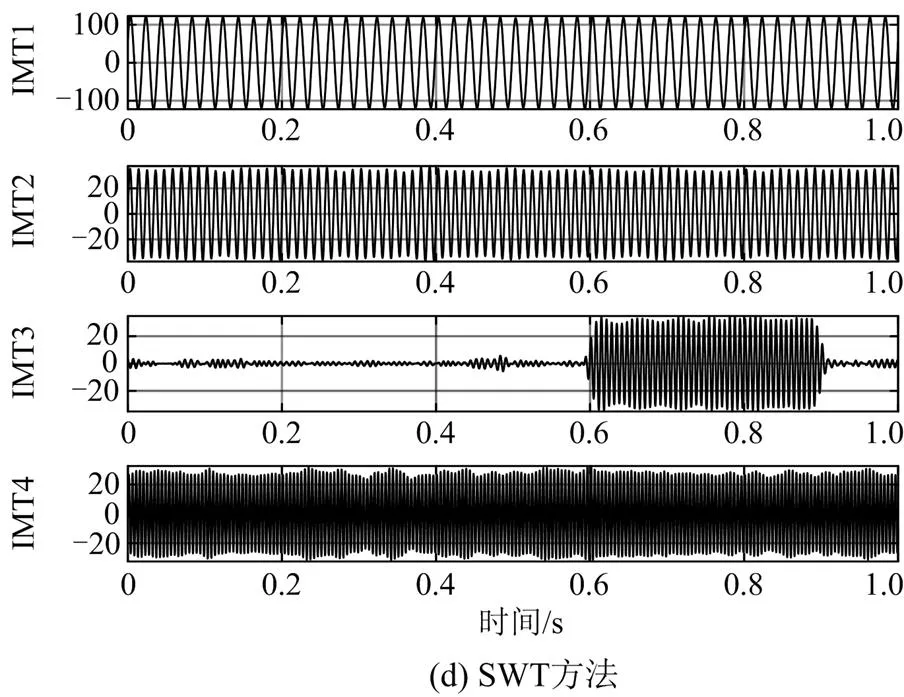
图6 模态分解结果(SNR=20 dB)
2.2 基波频率波动的仿真信号
设置采样时长为1.0 s,采样频率为4096 Hz,截取基波在前0.12 s的频率波动情况,如图7所示。
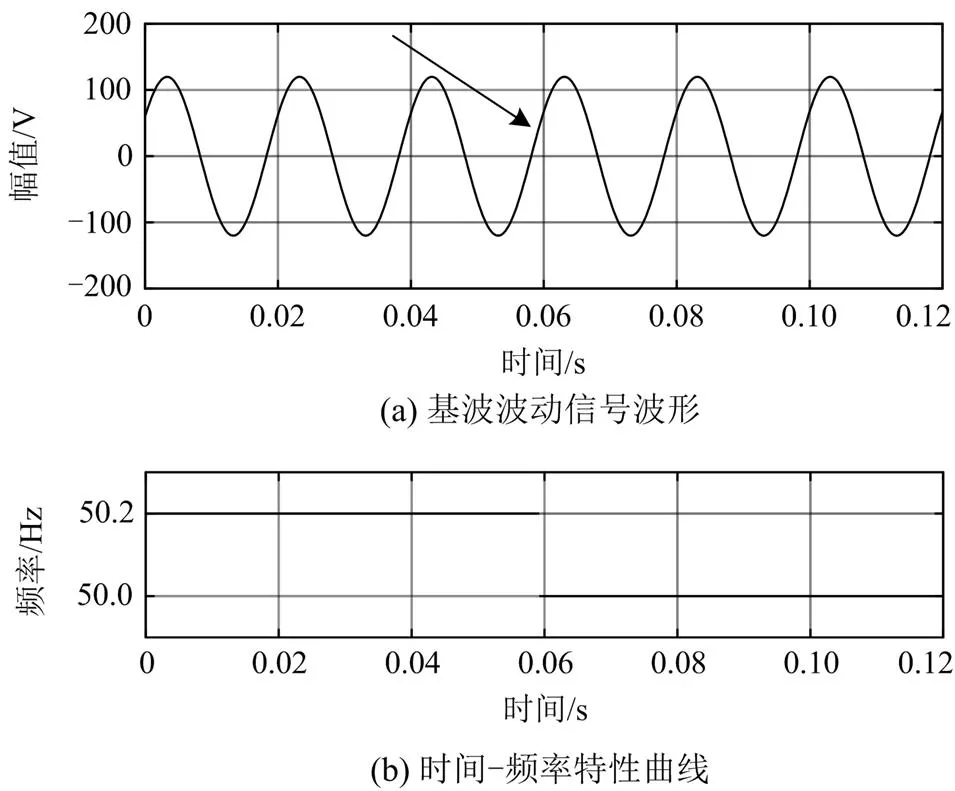
图7 基频波动(0~0.12 s)
由图7可以看出,图7(a)箭头指在基波波形的0.0591 s时刻位置,由图7(b)中基波在理想状态下的时间-频率特性曲线表明,该基波频率波动的信号分量在前0.0591 s时段内存在50.2 Hz的基波频率成分,在0.0591~1.0000 s时段存在50.0 Hz的基波频率成分,基波频率在前0.0591时段内存在波动。
分别用EMD、CEEMDAN、VMD和SWT对含有基波频率波动的暂态信号进行基波检测,所分解出的模态分量如图8所示。前6个周期(图8中箭头所截取的周期数)提取出的分量与原始基波的波形吻合效果如图9所示。
由图8和图9可知,EMD、CEEMDAN、VMD和SWT都能分解出基波,每种方法的IMF2、IMF3、IMF1、IMT1对应基波,但IMT1分量波形受基波波动导致的非同步采样影响更小,SWT和VMD所分解出的3次谐波在起止时刻存在抖动,SWT抖动更轻微;VMD所分解出的基波存在边界效应,起止峰值小于原始基波峰值,CEEMDAN和EMD出现了不同程度的模态混叠,峰值处存在不同大小的幅值,整体波形不整齐,基波波形吻合效果较差。
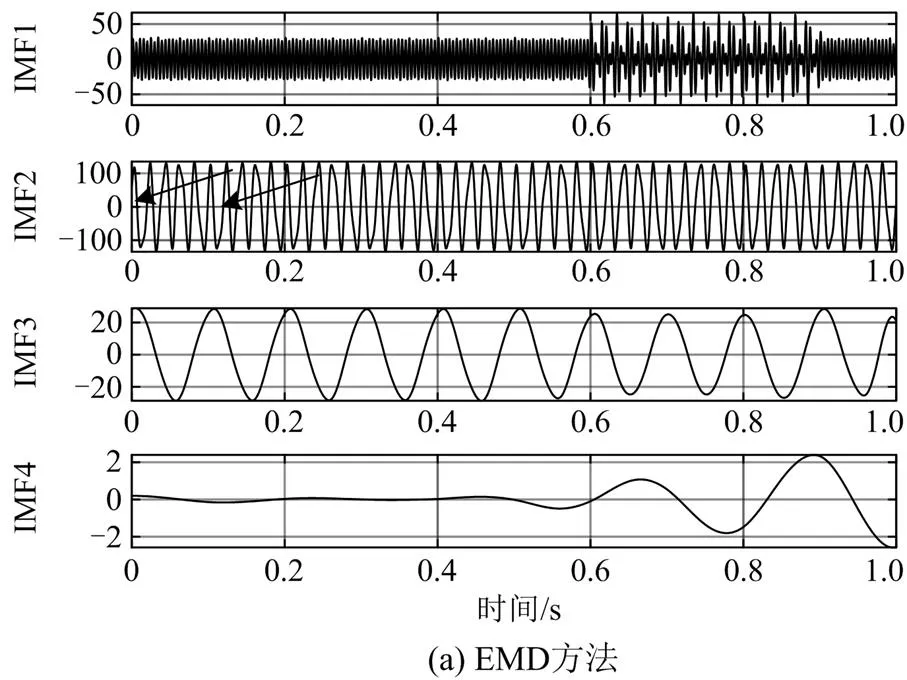
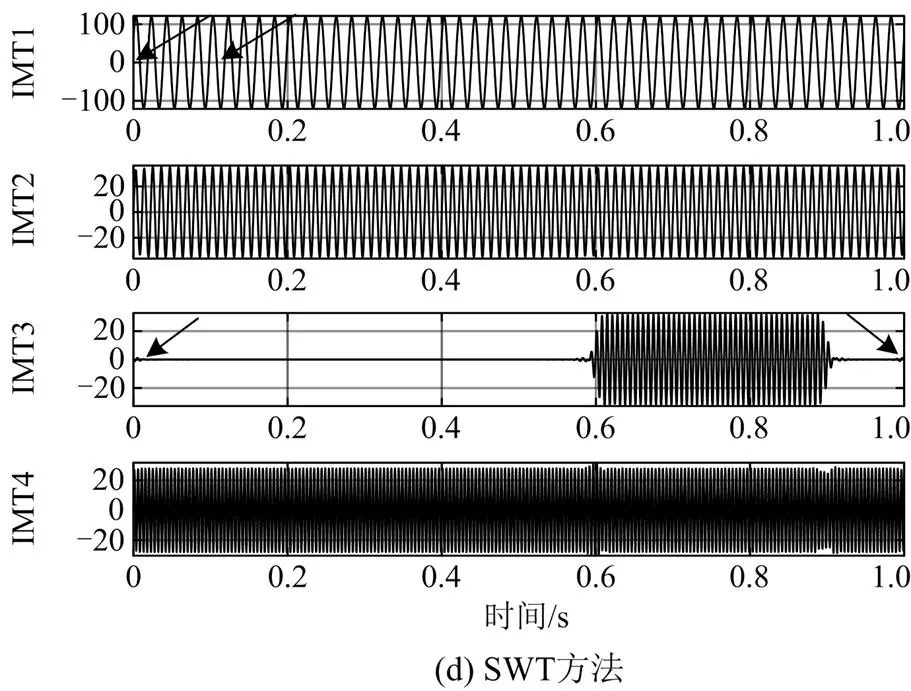
图8 模态分解结果(基频波动)
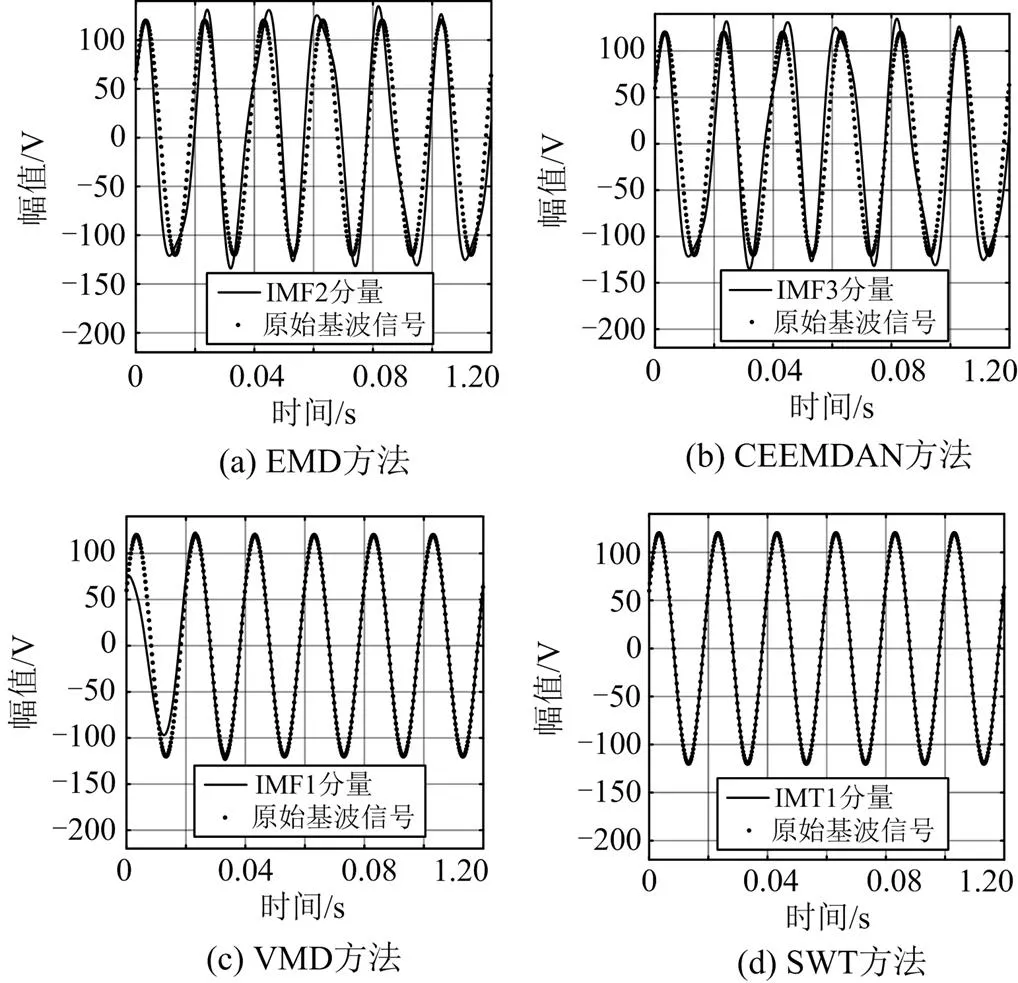
图9 基波波形吻合效果2
2.3 间谐波靠近基波和谐波的仿真信号
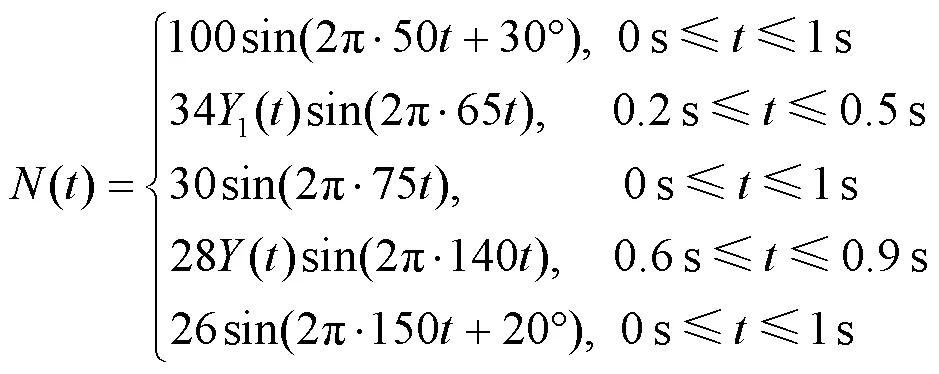
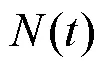
由图10可知,加入20 dB的高斯白噪声,EMD和CEEMDAN所分解的基波分量IMF4出现了不同程度的模态混叠,不能完全提取基波;VMD分解得到的基波分量IMF1也存在较明显的模态混叠,且左右端点处存在边界效应,其后3个模态分量信息已经被噪声淹没;而SWT分解的分量按能量从大到小排列,基波能量最大,所以第1个分量IMT1为基波,不像EMD系列是从高频到低频排列,必须对所有分解项进行参数分析,直至找到基波分量,SWT所分解的IMT1分量的频率为49.999 990 Hz。此外,在谐波和间谐波出现模态混叠的情形下,SWT依然能准确提取基波,表明其基波提取能力强于谐波和间谐波。4种方法抗噪的能力由强到弱排序为SWT>VMD>CEEMDAN>EMD。
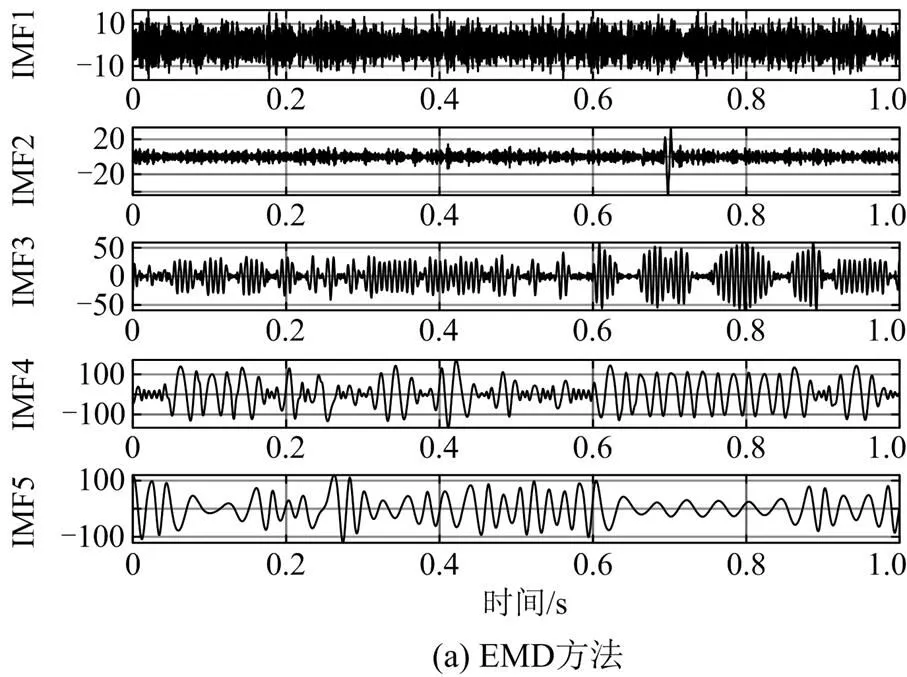
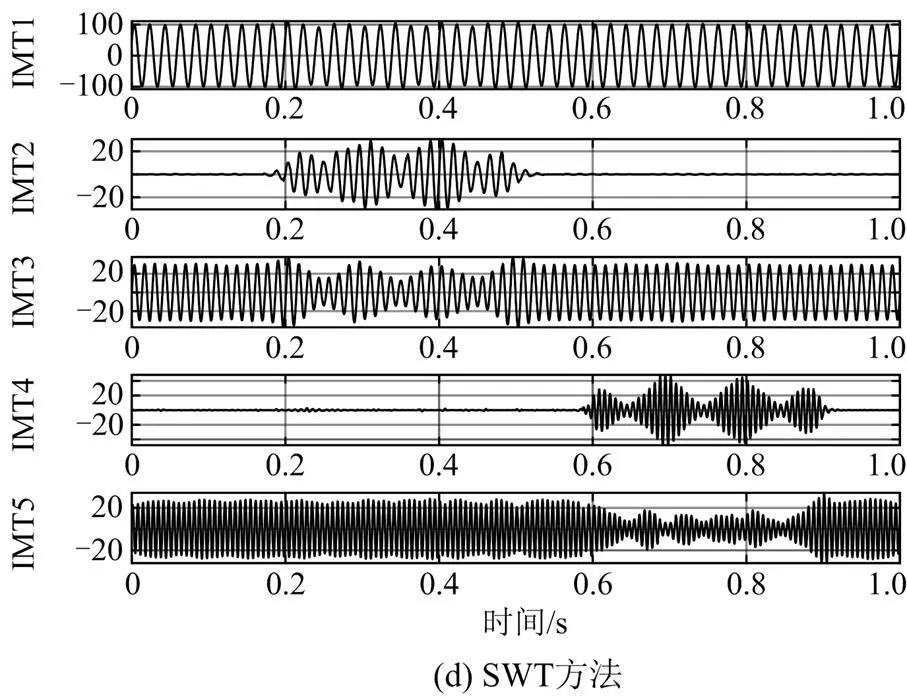
图10 模态分解结果(SNR=20 dB)
3 实验验证与分析
根据某牵引供电系统高压侧220 kV的A相瞬时电压实测数据,采样频率为20 kHz,采样时间间隔为50ms,信号长度为1 s,取其前0.2 s的信号长度,将SWT与EMD、CEEMDAN、VMD应用于实际信号,分解得到前4项模态分量波形如图11所示。
由图11可知,4种方法均能分解出基波,EMD、CEEMDAN、VMD、SWT分解得到的IMF4、IMF4、IMF1、IMT1分别对应基波,但EMD和CEEMDAN所分解出的第4个分量代表基波,存在分解分量的延迟,而SWT和VMD分解出的第1个分量即代表基波,基波检测效率更高;SWT分解出的IMT3和IMT4的频率分别为145.0145 Hz和250.0054 Hz,对应3次谐波和5次谐波,而剩余由其他3种方法分解出的模态分量则近似噪声。

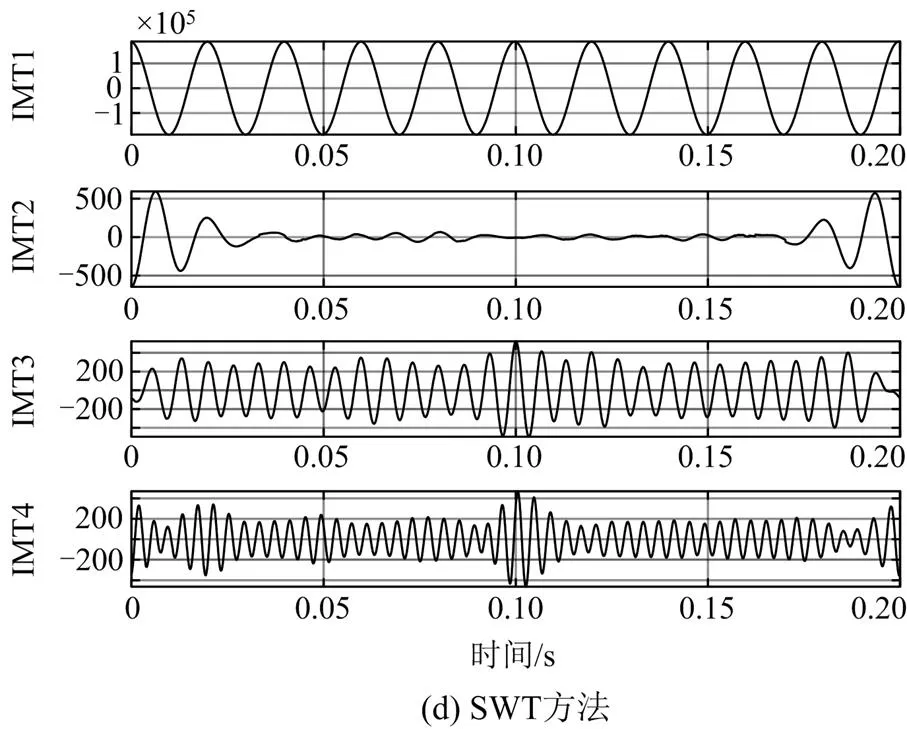
图11 模态分解结果(实测电压)
经Hilbert变换,得到4种方法的基波时间-频率特性曲线如图12所示。
由图12可知,SWT方法提取到的基波频率波动较其他3种方法更小,基波频率波动范围控制在49.7~50.3 Hz,波动幅度小于1 Hz,而其他3种方法的基波频率波动幅度则超过了4 Hz,表明本文方法适用于实际信号的频率检测。
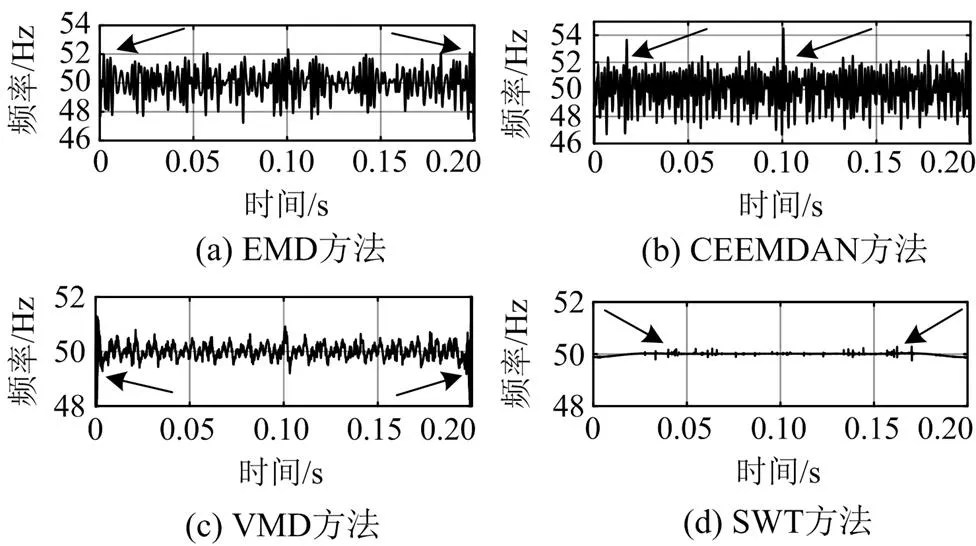
图12 基波时间-频率特性曲线
EMD、CEEMDAN、VMD和SWT的基波测量频率、标准差及其与原始基波频率标准值(50 Hz)之间所存在的相对误差如表3所示。

表3 4种方法的检测结果(实测电压)
由表3可知,实际A相电压信号经本文方法测量得到的基波频率与原始基波频率的相对误差5.2427×10-7较其他3种方法更小,精度达到10-7量级,其标准差为0.036 553,较其他3种方法的标准差也更小,测量结果更稳定,表明SWT能更为准确地从实际A相电压信号中检测出基波频率,另外,该方法测量出的基波幅值为1.872 433×105V。
4 结论
本文在谐波幅值瞬变、噪声混入、基波频率波动、间谐波频率靠近基波和谐波的情况下,基于SWT进行电力信号的基波提取,再通过Hilbert变换计算出基波频率和幅值,从而完成基波检测。
实验结果表明,在谐波幅值发生阶跃变化时, SWT通过同步挤压来避免频率曲线交叉,能够准确提取出基波分量,模态分解能力强,可以有效避免模态混叠;对于混有噪声的暂态信号,该方法仍能准确地测量基波特征参数,表明SWT具有较强的抗噪性,且基波的提取能力强于谐波和间谐波;本文也考虑了因基波频率波动导致采样不同步的情况,将所采用的SWT与EMD、CEEMDAN、VMD相对比,得到SWT测量出的基波频率和幅值受采样不同步的影响更小,与原始基波的波形吻合度更高的结论。
综上,SWT能准确地测量出基波参数,其分解出的第1个IMT分量即是基波,具有更强的抗噪能力,基波检测精度高于传统的时频分析方法,如EMD、CEEMDAN和VMD,频率精度最高可达10-8量级,且SWT基波提取的能力强于谐波和间谐波,是提取基波的有力工具。
[1] 秦毅, 秦树人, 毛永芳. 小波变换中经验模态分解的基波检测及其在机械系统中的应用[J]. 机械工程学报, 2008, 56(3): 135-142.
QIN Yi, QIN Shuren, MAO Yongfang. Fundamental wave detection based on wavelet transform and empirical mode decomposition with application in mechanical system[J]. Journal of Mechanical Engineering, 2008, 56(3): 135-142.
[2] 兰金晨, 朱革兰, 李松奕. 基于广义S变换突变识别的暂稳态谐波检测方法[J]. 电力系统保护与控制, 2020, 48(23): 40-46.
LAN Jinchen, ZHU Gelan, LI Songyi. Detection method of transient and steady state harmonics based on generalized S-transform mutation recognition[J]. Power System Protection and Control, 2020, 48(23): 40-46.
[3] 李宁, 左培丽, 王新刚, 等. 基于改进DFT和时域准同步的间谐波检测算法[J]. 电力自动化设备, 2017, 37(4): 170-178.
LI Ning, ZUO Peili, WANG Xingang, et al. Inter-harmonic detection based on improved DFT and time-domain quasi-synchronization[J]. Electric Power Automation Equipment, 2017, 37(4): 170-178.
[4] 孙仲民, 何正友, 臧天磊. 基于滑窗频谱分离算法的基波参数测量[J]. 中国电机工程学报, 2017, 37(19): 5604-5612, 5837.
SUN Zhongmin, HE Zhengyou, ZANG Tianlei. Estimating fundamental parameters by using sliding-window spectrum separation algorithm[J]. Proceedings of the CSEE, 2017, 37(19): 5604-5612, 5837.
[5] CHEN G L, TSAI S H, YANG K J. On performance of sparse fast Fourier transform and enhancement algorithm[J]. IEEE Transactions on Signal Processing, 2017, 65(21): 5716-5729.
[6] 陈至豪, 王立德, 王冲, 等. 基于组合余弦优化窗四谱线插值FFT的电力谐波分析方法[J]. 电网技术, 2020, 44(3): 1105-1113.
CHEN Zhihao, WANG Lide, WANG Chong, et al. An approach for electrical harmonic analysis based on optimized composite cosine window four-spectrum-line interpolation FFT[J]. Power System Technology, 2020, 44(3): 1105-1113.
[7] 王燕. 电能质量扰动检测的研究综述[J]. 电力系统保护与控制, 2021, 49(13): 174-186.
WANG Yan. Review of research development in power quality disturbance detection[J]. Power System Protection and Control, 2021, 49(13): 174-186.
[8] DESAI J P, MAKWANA V H. A novel out of step relaying algorithm based on wavelet transform and a deep learning machine model[J]. Protection and Control of Modern Power Systems, 2021, 6(4): 500-511.
[9] VINAYAK B A, ANAND K A, JAGADANAND G. Wavelet-based real-time stator fault detection of inverter-fed induction motor[J]. IET Electric Power Applications, 2020, 14(1): 82-90.
[10] HUANG N E, SHEN Z, LONG S R. New view of nonlinear water waves: the Hilbert spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31: 417-457.
[11] LÜ Chenhuan, ZHAO Jun, WU Chao, et al. Optimization of the end effect of Hilbert-Huang transform (HHT)[J]. Chinese Journal of Mechanical Engineering, 2017, 30(3): 732-745.
[12] WU Z, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.
[13] 温志平, 方江雄, 刘军, 等. 基于CEEMDAN和SWT的地震信号随机噪声压制[J]. 地球物理学进展, 2019, 34(3): 949- 960.
WEN Zhiping, FANG Jiangxiong, LIU Jun, et al. Seismic random noise attenuation based on CEEMDAN and SWT[J]. Progress in Geophysics, 2019, 34(3): 949-960.
[14] 张慧, 孟克其劳, 张占强, 等. 基于CEEMDAN和HHT的谐波检测方法[J]. 电子测量技术, 2020, 43(6): 83-87.
ZHANG Hui, MENG Keqilao, ZHANG Zhanqiang, et al. Harmonic detection method based on CEEMDAN and HHT[J]. Electronic Measurement Technology, 2020, 43(6): 83-87.
[15] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
[16] 郎宪明, 朱永强, 李金娜, 等. 基于时频分析和改进差分进化的多点泄漏定位方法[J]. 振动与冲击, 2022, 41(1): 39-45, 87.
LANG Xianming, ZHU Yongqiang, LI Jinna, et al. Multi-point leakage locating method based on TFA and improved DE[J]. Journal of Vibration and Shock, 2022, 41(1): 39-45, 87.
[17] DAUBECHIES I, LU J, WU H. Synchrosqueezed wavelet transforms: an empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis, 2010, 30(2): 243-261.
[18] 喻敏, 王斌, 王文波, 等. 基于SST的间谐波检测方法[J]. 中国电机工程学报, 2016, 36(11): 2944-2951.
YU Min, WANG Bin, WANG Wenbo, et al. An inter- harmonic detection method based on synchrosqueezing wavelet transform[J]. Proceedings of the CSEE, 2016, 36(11): 2944- 2951.
[19] 刘博文, 张新燕, 常喜强, 等. 基于SWT的风电汇集地区非同步振荡PMU暂态录波数据分析[J]. 太阳能学报, 2020, 41(1): 217-224.
LIU Bowen, ZHANG Xinyan, CHANG Xiqiang, et al. Analysis of non-synchronous oscillation based on SWT and transient wave recorded data of PMU in wind farm integration area[J]. Acta Energiae Solaris Sinica, 2020, 41(1): 217-224.
[20] 熊炘, 占锐, 王小静. 同步压缩小波与希尔伯特-黄变换性能对比[J]. 振动·测试与诊断, 2015, 35(6): 1103-1109.
XIONG Xin, ZHAN Rui, WANG Xiaojing. Performance comparison between synchronous compressed wavelet and Hilbert-Huang Transform[J]. Vibration·Testing and Diagnosis, 2015, 35(6): 1103-1109.
[21] 喻敏, 王斌, 王文波, 等. 基于同步挤压小波变换的电力系统时变谐波检测[J]. 电工技术学报, 2017, 32(增刊1): 50-57.
YU Min, WANG Bin, WANG Wenbo, et al. Power system time-varying transient harmonics detection based on SWT[J]. Transactions of China Electrotechnical Society, 2017, 32(S1): 50-57.
[22] 刘景良, 任伟新, 王佐才, 等. 基于同步挤压小波变换的结构瞬时频率识别[J]. 振动与冲击, 2013, 32(18): 37-42, 48.
LIU Jingliang, REN Weixin, WANG Zuocai, et al. Instantaneous frequency identification based on synchrosqueezing wavelet transformation[J]. Journal of Vibration and Shock, 2013, 32(18): 37-42, 48.
[23] IATSENKO D, MCCLINTOCK P V E, STEFANOVSKA A. Nonlinear mode decomposition: a noise-robust, adaptive decomposition method[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2015, 92(3): 1-25.
[24] 李欣悦, 李凤婷, 尹纯亚, 等. 直流双极闭锁故障下送端系统暂态过电压计算方法[J]. 电力系统保护与控制, 2021, 49(1): 1-8.
LI Xinyue, LI Fengting, YIN Chunya, et al. Transient overvoltage calculation method of HVDC sending-end system under DC bipolar blocking[J]. Power System Protection and Control, 2021, 49(1): 1-8.
[25] 毛宇阳, 杨志. V2X双向充电机在微电网中的控制策略[J]. 新能源汽车供能技术, 2021, 5(1): 19-22.
MAO Yuyang, YANG Zhi. Control strategy of V2X bidirectional charger in microgrid[J]. Energy Supply Techniques of New Energy Vehicles, 2021, 5(1): 19-22.
[26] 马也驰, 陈隆道. 应用于频率波动电网的改进相位差校正法[J]. 电力系统保护与控制, 2018, 46(9): 136-145.
MA Yechi, CHEN Longdao. An improved phase correction difference method applied to the power systems with frequency fluctuation[J]. Power System Protection and Control, 2018, 46(9): 136-145.
[27] 电能质量电力系统频率偏差: GB/T 15945—2008[S]. 北京: 中国标准出版社, 2008.
Power quality-frequency deviation for power system: GB/T 15945—2008[S]. Beijing: Standards Press of China, 2008.
[28] 倪大志. 电源质量影响仪表测量准确度[J]. 计量与测试技术, 2010, 37(12): 53-55.
NI Dazhi. Power quality affects the meter measuring accuracy[J]. Metrology & Measurement Technique, 2010, 37(12): 53-55.
[29] XU D, LIU P F, CHEN Z P. Damage mode identification and singular signal detection of composite wind turbine blade using acoustic emission[J]. Composite Structures, 2021, 255: 1-16.
[30] 赫玉莹, 王学华, 刘福鑫. LCL型并网逆变器分裂电流单环控制及其强鲁棒性权值设计[J]. 中国电机工程学报, 2021, 41(10): 3536-3546, 3678.
HE Yuying, WANG Xuehua, LIU Fuxin. Splitting current single-loop control and robust weight value design for LCL-type grid-connected inverter[J]. Proceedings of the CSEE, 2021, 41(10): 3536-3546, 3678.
Fundamental detection for a power system based on SWT
TAO Jialan1, 2, YU Min1, 2, CHEN Guici1, 2, WANG Bin3
(1.Hubei Province Key Laboratory of Systems Science in Metallurgical Process, Wuhan University of Science and Technology,Wuhan 430065, China; 2. College of Science, Wuhan University of Science and Technology, Wuhan 430065, China; 3. College of Information and Engineering, Wuhan University of Science and Technology, Wuhan 430081, China)
When noise is mixed into a signal containing the fundamental component, the traditional time-frequency analysis method is prone to modal aliasing in the fundamental component extraction process. To accurately detect the fundamental component, synchrosqueezing wavelet transform (SWT) with high accuracy of time-frequency analysis is applied to realize the fundamental detection. First, the signal containing the fundamental component is decomposed into a set of intrinsic mode type functions (IMTs) by SWT. The first component IMT1 represents the fundamental. Then, the fundamental frequency and amplitude are measured by Hilbert Transform. Finally, the algorithm is verified in the situation of harmonic amplitude transient, noise mixing, fundamental frequency fluctuation and interharmonic frequencies near the fundamental and harmonic frequencies. The experimental results show that SWT can accurately extract the fundamental component, and the frequency accuracy can reach 10-8orders of magnitude. The method has strong noise resistance and is better at extracting the fundamental component than harmonics and interharmonics.
fundamental detection; mode aliasing; SWT; Hilbert transform; noise resistance
10.19783/j.cnki.pspc.211660
2021-12-06;
2022-03-08
陶佳兰(1997—),女,硕士研究生,研究方向为电能质量扰动检测;E-mail: jlantao_21@163.com
喻 敏(1975—),女,通信作者,博士,讲师,研究方向为分形与小波应用、电能质量扰动检测等;E-mail: yufeng3378@163.com
陈贵词(1978—),男,博士,教授,研究方向为随机系统、鲁棒控制等。E-mail: gcichen@yahoo.com.cn
国家自然科学基金项目资助(51877161,61671338);冶金工业过程系统科学湖北省重点实验室基金重点项目资助(Y202007,Z201901)
This work is supported by the National Natural Science Foundation of China (No. 51877161 and No. 61671338).
(编辑 许 威)
