路基下空洞的有限元动力模拟与分析

徐建国，王 斌，蔡迎春，王复明

(郑州大学 水利与环境学院 道检中心，郑州 450002)

便携式落锤弯沉仪(Portable Falling Weight Deflectometer，简称PFWD)是目前国际上普遍采用的结构强度无损检测仪器(图1)。其特点是:检测快、测试数据客观、精度高、便于携带、操作简单、自动化程度高，适用范围广、无破损、影响深度大，能够直接反映现场实际情况等。PFWD主要用于路基路面、铁路、机场、港口、城市交通及工业与民用建筑等检测领域。在道路勘察设计和施工过程中，经常会遇到设计路基下方存在各种类型的地下空洞，地下空洞这种不良地质现象的存在常使路基失稳，严重时会造成路基、路面、涵洞等构筑物的破坏。所以，如何准确地找出这些病害的位置及分析其大小成为工程界一直关注的课题。本文根据有限元动力分析原理，对地表下既有空洞的情况进行正演模拟，通过对PFWD动载作用下的时程曲线进行分析，据此来探索查找空洞的位置和大小的方法。

图1 便携式落锤弯沉仪(PFWD)

1 有限元动力分析原理

由于采用PFWD对压实度较好的路基进行冲击荷载试验时，路基的塑性变形较小，故本文采用三维弹性体模型模拟路基变形。在动荷载作用下的弹性体介质内，其动力控制微分方程为

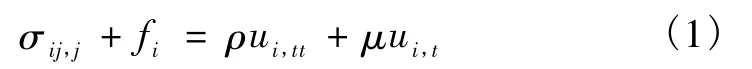
式中，σij，j是在坐标系 x1、x2、x3中应力张量 σij对独立坐标xj求偏导数;fi为 i方向的外力;ρ是质量密度;μ是阻尼系数;ui，tt和 ui，t分别是 ui对 t的二次导数和一次导数，即分别表示i方向的加速度和速度。

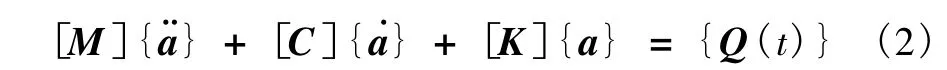
对式(1)采用有限元求解，可以得到弹性半空间的系统动力有限元平衡方程式中，［M］、［C］、［K］分别是弹性半空间系统的质量矩阵、阻尼矩阵和刚度矩阵;分别是加速度向量、速度向量和位移向量;{Q(t)}是动荷载。

岩土材料本构关系明显与加载速度有关，显然这是黏性因素的影响。本文本构关系中的模量采用等效动弹模量，可根据实测数据反演而得。黏性因素由阻尼矩阵体现，本文采用 Rayleigh阻尼，即单元阻尼阵［C］e=α［M］e+β［K］e，α = ξω1，β = ξ/ω1，上标 e表示矩阵为单元矩阵，ξ为阻尼比，ω1为结构的基频。对于式(2)采用无条件稳定的隐式算法Newmark法进行求解。

Newmark积分方法实质上是线性加速度法的一种推广。它采用下列假设

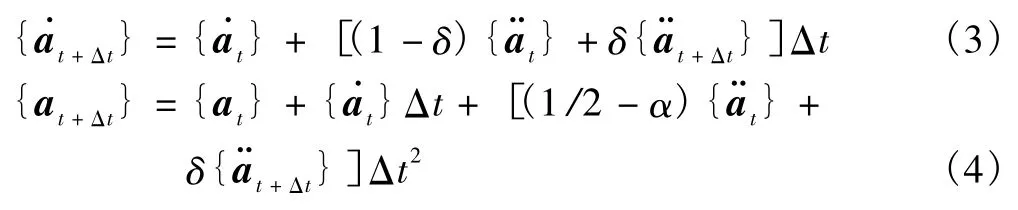
其中，α和δ是按积分精度和稳定性要求而决定的参数。由式(4)解得

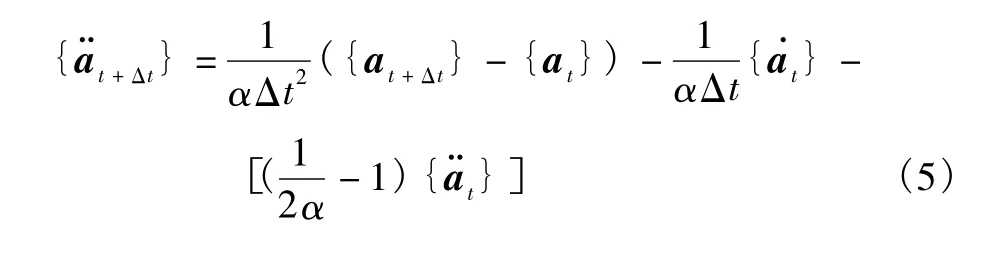
将式(5)带入式(3)，然后再代入式(2)，则得到从at、计算at+Δt的公式

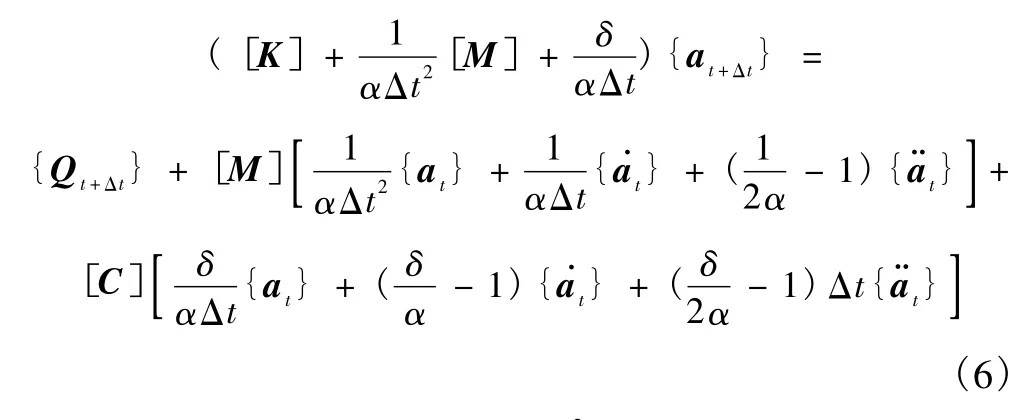
当 δ≥0.5，α≥0.25(0.5+ δ)2时，Newmark 方法无条件稳定。

2 分析模型与程序验证

由于PFWD的影响深度在70 cm左右，所以，在PFWD冲击荷载作用下，建立水平方向6 m×6 m，厚度为4 m的三维长方体模型可以满足精度要求。对模型进行有限元划分选用六面体8节点等参单元，每个单元8个高斯点，对模型进行划分共计8 000个单元，9 621个节点，剖面示意如图2所示(图2中变量见3.1)。由于空洞的存在使不同工况下单元及节点稍有不同。有限元底边边界条件按固结考虑，侧面采用黏性边界即设置黏性阻尼器来模拟水平方向的无限性。

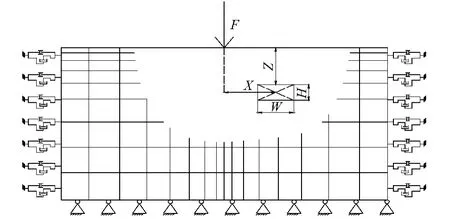
图2 三维模型剖面示意

根据动力有限元原理和模型采用Fortran90语言编制了相应的有限元正演程序。由于地形边界的不规则性，使几何模型的建立与划分的程序实现的通用性差，而ANSYS在模型的网格划分功能很强大，所以模型建立与网格划分采用ANSYS的参数设计语言(APDL)编写相应的宏命令文件，然后用 Fortran90编写模块调用ANSYS生成的CDB文件的网格信息。

为验证有限元正演程序的模拟效果，在没有空洞的路基上用PFWD进行了测试。作用荷载为PFWD冲击荷载，如图3所示，测试所得的时程曲线如图4实线所示。在相同动荷载作用下用有限元正演程序计算的时程曲线如图4中虚线所示，两者吻合较好，表明了正演程序的有效性。

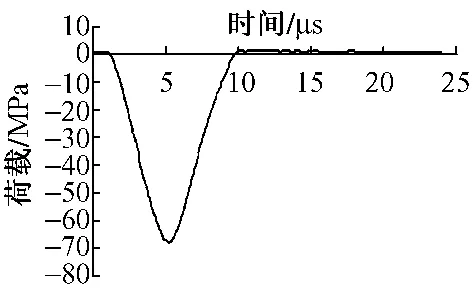
图3 PFWD冲击荷载

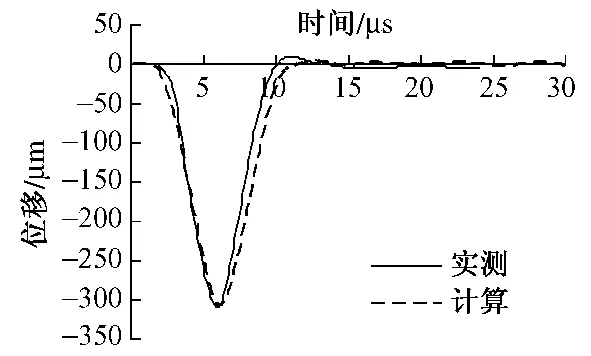
图4 时程曲线对比

3 路基下存在空洞的动力模拟与分析

3.1 分析工况

路基下空洞三维空间模型的xoz剖面示意如图2所示，影响PFWD时程曲线特性与空洞有关的因素可归纳为:①空洞的高度H;②空洞的宽度W;③空洞的埋深Z;④PFWD作用位置的中心线位置到空洞中心的距离X;⑤空洞的横截面面积A;⑥F为PFWD施加的荷载。为了便于讨论，不特别说明先假设空洞为长方体。下面分四种工况进行讨论，其中空洞的宽度和横截面积合为一个工况进行。

3.2 空洞的高度变化对动力响应的影响

模型中空洞高度分别取 10、20、30、40、50 cm，在图5中依次用 H1、H2、H3、H4和 H5表示。荷载作用在空洞正上方，空洞埋深及横截面积大小固定不变时，对其进行正演模拟，得到相应的空洞高度变化对时程曲线的影响，如图5所示。从图5可以看出，空洞高度的变化对时程曲线没有明显的影响，仅影响作用荷载结束后的波形略有变化。由此可见，在其它因素确定的情况下，仅空洞的高度H变化对时程曲线影响甚微。

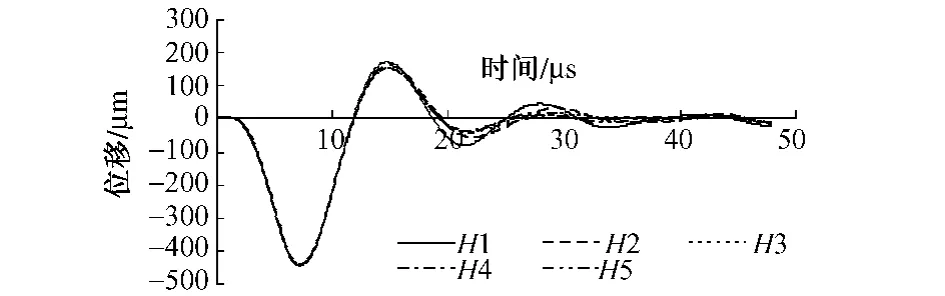
图5 空洞高度对时程曲线的影响

3.3 空洞的横截面变化对动力响应的影响

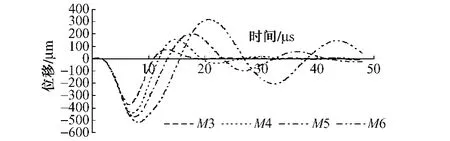
图6 空洞横截面对时程曲线的影响

空洞在水平方向的横截面积取20 cm×20 cm、25 cm×25 cm、30 cm×30 cm和35 cm×35 cm，在图6中依次用M3、M4、M5及 M6表示。作用荷载位于正上方，埋深和空洞高度固定，对其进行正演模拟，得到相应的空洞横截面变化对时程曲线的影响曲线。从图6可以看出，当埋深固定时，空洞水平横截面越大，时程响应曲线的位移值也越大，而且使最大位移峰值向后延迟明显，对于第一个半波最大位移变化和时间延迟数据如表1所示。

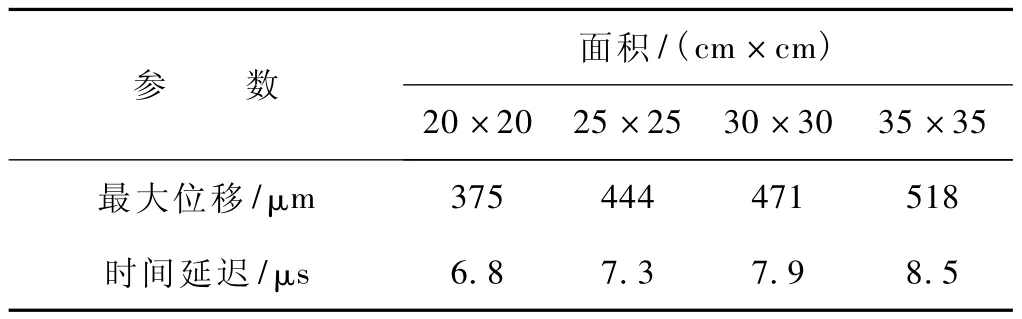
表1 空洞横截面对时程曲线的影响

3.4 空洞的埋深变化对动力响应的影响

PFWD动荷载作用在40 cm×40 cm×20 cm的空洞的正上方，埋深对时程曲线的影响如图7所示，其中Z 代表埋深，Z1=20 cm，Z2=25 cm，Z3=30 cm，Z4=35 cm，Z5=40 cm。从图7可以看出，随着空洞埋深的变化时程曲线发生了明显的变化，对于第一个半波的最大位移变化和时间延迟数据如表2所示。由第一个半波的变化可以看出当空洞埋深<40 cm时，空洞对时程曲线影响比较明显，当埋深比较大时时程曲线变化不太明显，是由于PFWD的影响深度只有70 cm左右，所以空洞的影响深度比较小。对于较深的空洞缺陷，可以采用更大的作用荷载以便显示缺陷对时程曲线的影响，从而判断空洞的位置。

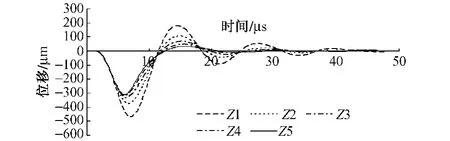
图7 空洞埋深对时程曲线的影响

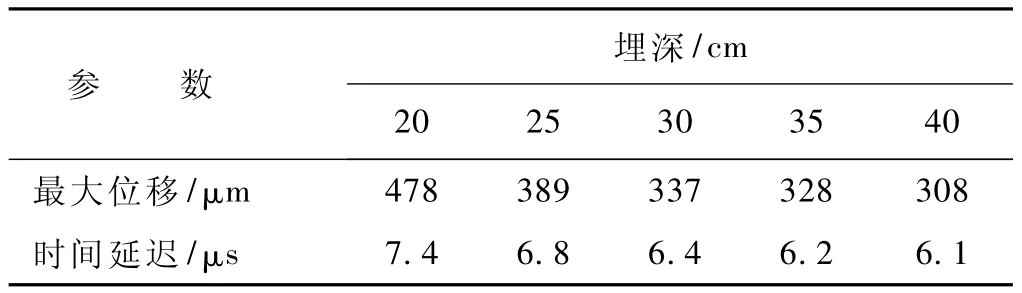
表2 空洞埋深对时程曲线的影响

3.5 作用荷载位置变化对动力响应的影响

由图8可以看出，空洞位置与大小固定时，改变作用荷载的位置对时程曲线的影响，其中F代表动荷载作用的位置偏离空洞正上方的位移，F0=0，F1=10 cm，F2=20 cm，F3=30 cm，F4=40 cm，时程曲线发生了明显的变化，时间延迟较小，位移变化较大，对于第一个半波最大位移变化和时间延迟数据如表3所示。这对确定空洞的位置提供了依据，当荷载作用在空洞的上方时，时程曲线的峰值明显增大，波动明显变化。

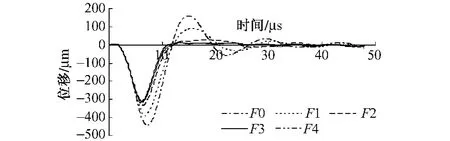
图8 作用荷载位置对时程曲线的影响

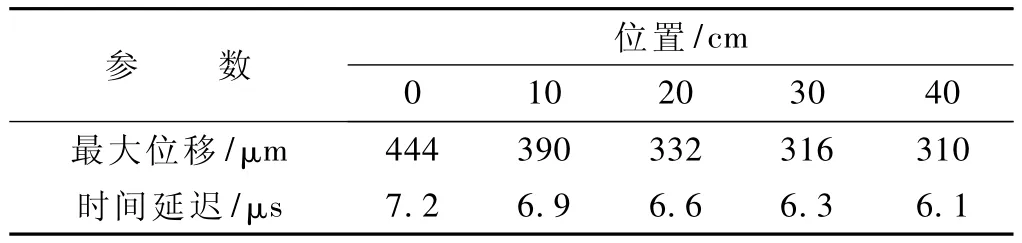
表3 作用荷载位置对时程曲线的影响

4 结论

本文基于编写的有限元动力分析程序对路基下空洞模型进行了数值模拟，计算结果显示，该方法能够有效地反应空洞对时程曲线的影响。通过各工况时程曲线的分析可得出如下结论:当路基下存在空洞缺陷时，可通过便携式落锤弯沉仪(PFWD)的荷载作用位置的变化来确定空洞在水平方位;空洞的埋深和空洞上表面的大小对时程曲线的影响较大;空洞高度方向的变化对时程曲线没有太大的影响;随着作用荷载大小的不同，空洞深度对时程曲线的影响有一定的范围。这些结论为判断空洞的大小、位置、埋深等提供了技术依据，同时也为下一步的基于正演模型的空洞反演分析提供了技术支持。

[1] 王勖成，邵敏.有限单元法基本原理和数值方法［M］.北京:清华大学出版社，1997.

[2] R W克拉夫，J彭津.结构动力学［M］.北京:科学出版社，1981.

[3] 刘俊，蔡迎春，王复明.路基下目标的路面雷达电磁波模拟与分析［J］.大连海事大学学报，2009，35(1):99-102.

[4] 彭芳乐，清主真.空洞的存在对浅基础承载力与沉降的影响分析［J］.岩石力学与工程学报，2007，26(6):1123-1131.