因子分析教学案例的改进

李俊扬林海明

（1.贵州师范大学 数学与计算机科学学院，贵阳 550001；2.广东商学院a.经济贸易与统计学院；b.国民经济研究中心，广州 510320；3.广东省电子商务市场应用技术重点实验室，广州 510320)

1 因子分析模型L用于综合评价的步骤与实例

对于多元统计问题的解决，计算出有关模型的结果是一方面，同时能通过计算结果、原始数据进行数据分析，尽可能地解决实际问题同样是重要的。以下给出初始因子、旋转后因子较系统的应用步骤和实例。关于变量的总体相关阵通常是不知道的，通常用变量的样本相关阵替代。

因子分析模型L及其解和优良性，数学符号见文献[1]。

1.1 初始因子分析的综合评价步骤及其实例

初始因子应用于综合评价的步骤。

⑴指标的正向化(单独计算)[2]，标准化；

⑵求变量的样本相关阵∑及其特征值λi，主成分法下的初始因子载荷阵L0，旋转后因子载荷阵LΓ；

⑶LΓ(要计算出多个 LΓ)与 L0比较，用因子载荷绝对值 0、1两极分化频数对比表判断(见表4)，如果L0中行元素绝对值足够向0、1两极分化，用初始因子进行分析[3]，继续[原始变量之间相关度很低或无关时，直接进行逐个指标分析，用∑i=1pXi作综合分析(Xi是正向化、标准化的)是适合的]。

⑷确定初始因子个数m：用L0和因子与变量显著相关的临界值判断，若因子与某些变量显著相关，则选入该因子[3]，因子个数m、因子方差累计贡献率随之确定；

⑸初始因子fi0的命名及其正向化：由L0的第i列li0，将与fi0显著相关的变量归为fi0一类，由这些变量的意义对因子fi0进行命名(注意有些变量，可能与两个因子显著相关，命名中、分析中也要同时考虑好这些变量的联系性影响)。正向化[3]：如果这类变量与fi0的相关系数表明该类变量的意义是正向的，fi0不变符号；如果意义是反向的，fi0、li0同时乘上负号；

⑹计算写出初始因子 F0=(λ1-1/2a1'X,…，λm-1/2am'X)'(用 L0回归的因子得分)；

⑺因为因子不相关，综合起来可反映样品的因子累加综合状况(不是反映多变量信息最大化时的样品值状况)，以初始因子方差贡献率λi/p为权数得综合初始因子

⑻计算给出m个初始因子样品值矩阵Hm0、综合初始因子样品值并排序；

⑼用m个初始因子样品值做聚类分析，按综合初始因子样品值排名顺序给出样品分类结果；[2]

⑽结合样品的分类结果，综合初始因子、初始因子样品值和排序，原始数据，原始变量的意义，进行优势、劣势、潜力状况和影响因素等的综合评价，给出较客观、可靠的决策相关性建议。

SPSS软件初始因子有关结果计算过程：原始数据的正向化数据输入或拷贝到数据窗口中，选择Analyze→Date Reduction→Factor→变量框中选入正向化的数据→Descriptives 选择 Initial solution，Coeffi-cients，Continue→Extraction 选择 Principal Component，Correlation matrix(数据标准化被 执 行 )，Numberoffactor：m，Unrotated factorsolution，Screen Plot(碎石图),Continue→Rotation 选择 None，Continue→Scores选择 Save as Variables，Regression，Display factor score coefficient matrix，Continue→OK。

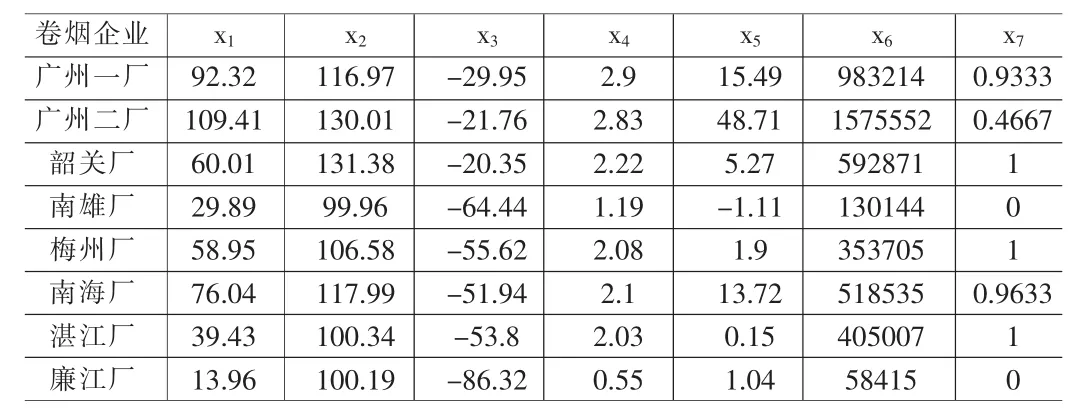
表1 原始数据正向化数据

计算结果有：样本相关系数阵R、R的特征值、初始因子载荷阵、初始因子的标准化变量系数阵、初始因子的样品值数据等，数据窗口中的fac1-1,…,facm-1为初始因子f10,…,fm0的样品值(注意Extraction选择Principal Component)。

旋转后因子载荷阵的计算要用下述1.2中SPSS软件旋转后因子有关结果计算过程。

例1.1[4]：2001年广东卷烟工业企业广州卷烟一厂、广州卷烟二厂、韶关卷烟厂、南雄卷烟厂、梅州卷烟厂、南海卷烟厂、湛江卷烟厂和廉江卷烟厂(n＝8)的经济效益变量为：x1-总资产贡献率、x2-资本保值增值率、x3-资产负债率、x4-流动资产周转率、x5-成本费用利润率、x6-全员劳动生产率、x7-产品销售率(p＝7)，数据见表1。对这些企业作经济效益综合评价。

⑴正向化数据为表1(x3正向化公式为：－x3。中性指标x7正向化公式为：

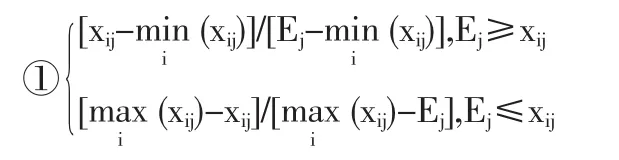
Ej为公认最好的中性值，这里Ej=1，其余是正向的；或②[|(xij/Ej)-1|+1]-1。表1 x7的正向化用公式①)。

⑵启用SPSS11.0软件因子分析过程进行因子分析，输入例1正向化表1的数据，得特征值表2，相关阵特征值碎石图图1，初始因子载荷阵L0、旋转后因子载荷阵LΓ表3。

⑶表3的L0、LΓ比较得表4,即L0每列系数绝对值较往0、1两极分化，故使用初始因子。

⑷前2个初始因子设为f10,f20,变量正态分布下，取显著水平为5%，显著相关的临界值是r(6)=0.707[8]，由L0和显著相关的临界值r(6)判断，因子f10，f20与变量显著相关；其它初始因子与变量没有显著相关，故因子个数m=2,此时累计贡献率为93.56%。

⑸因子的命名与正向化：初始因子设为 f10，f20，根据表3的L0,因子f10与x1-总资产贡献率、x2-资本保值增值率、x3-资产负债率、x4-流动资产周转率、x5-成本费用利润率、x6-全员劳动生产率显著正相关,故称f10为内部效益因子；因子f20与x7-产品销售率显著正相关,故称f20为外向效益因子。f10与f20为正向的。

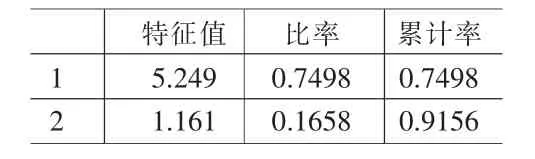
表2 相关阵特征值

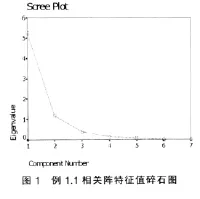
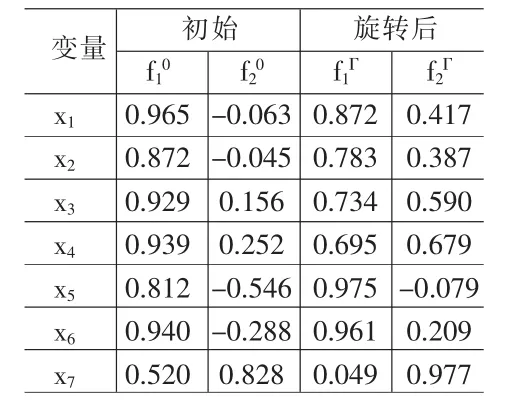
表3 因子载荷阵

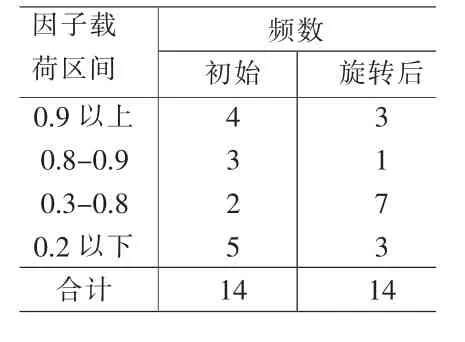
表4 因子载荷绝对值0、1两极分化频数对比表

⑹从初始因子得分系数得因子(Xi是xi的正向化、标准化变量)：

⑺以初始因子贡献率为权数构造综合因子函数：

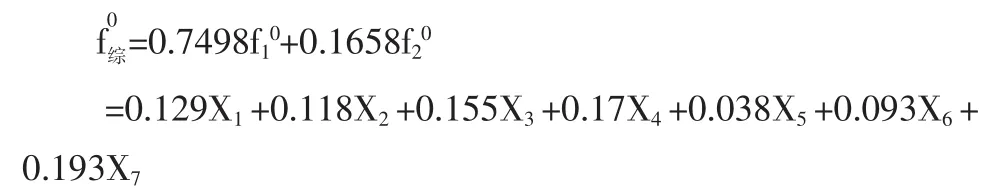
70.193)，X4-流动资产周转率(0.17)、X3(正向化)-融资率(0.155)、X1-总资产贡献率(0.129)的有效性，拉动的是X2-资本保值增值率(0.118)、X6-全员劳动生产率(0.093)、X5-成本费用利润率(0.038)。

⑻计算各企业因子值、综合因子值及排名见表5。

⑼将表5中无相关性的数据f10、f20作系统聚类分析，用欧氏距离、类平均法,按综合初始因子值相应顺序企业分为如下四类。

第一类：广州卷烟二厂；

第二类：广州卷烟一厂、韶关卷烟厂、南海卷烟厂；

第三类：梅州卷烟厂、湛江卷烟厂；

第四类：南雄卷烟厂、廉江卷烟厂。

⑽现结合聚类分析结果、表5、初始因子得分系数、表1进行第一类、第三类（其余类似）综合实证，提出建议。评价中注意初始因子得分系数：x5-成本费用利润率既对内部效益因子f10是好影响(系数为0.155)，又对外向效益因子f20有较大的负影响(系数为－0.47)。

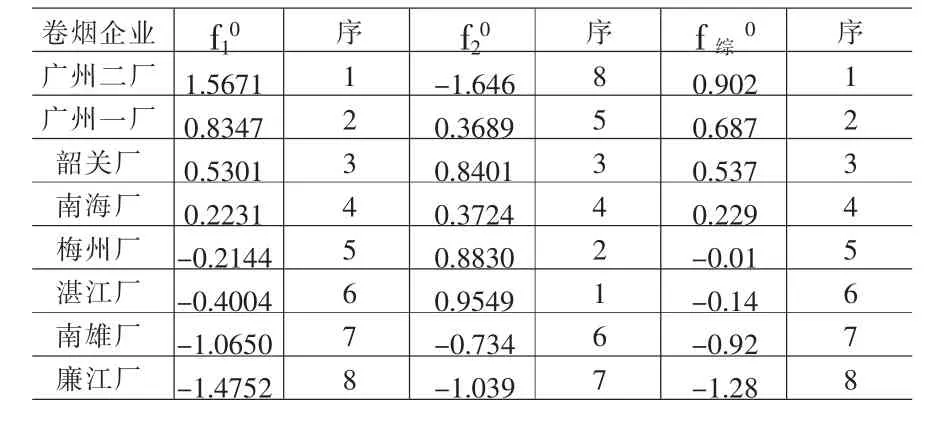
表5 初始因子、综合初始因子值及排名

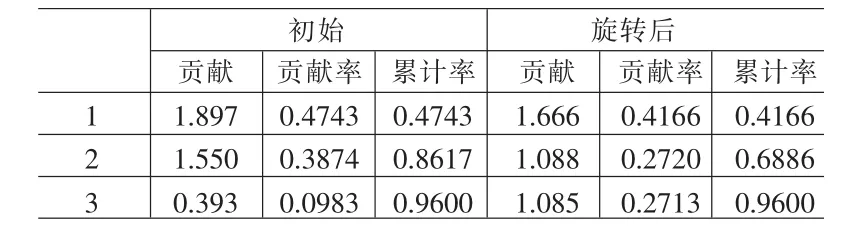
表6 因子方差贡献

建议：广州卷烟二厂应继续保持发挥x1-总资产贡献率、x2-资本保值增值率、x3-资产负债率、x4-流动资产周转率、x5-成本费用利润率、x6-全员劳动生产率(内部效益因子)已有优势的条件下，加强销售力度，提高x7-产品销售率(外向效益因子)，定能进一步提高综合效益，增强竞争力。

建议：梅州卷烟厂、湛江卷烟厂应明确已有差距、挖掘内部管理与产品质量潜力，在既抓好自身已有立足的前提下,向省内外卷烟企业优点学习,提高综合经济效益。

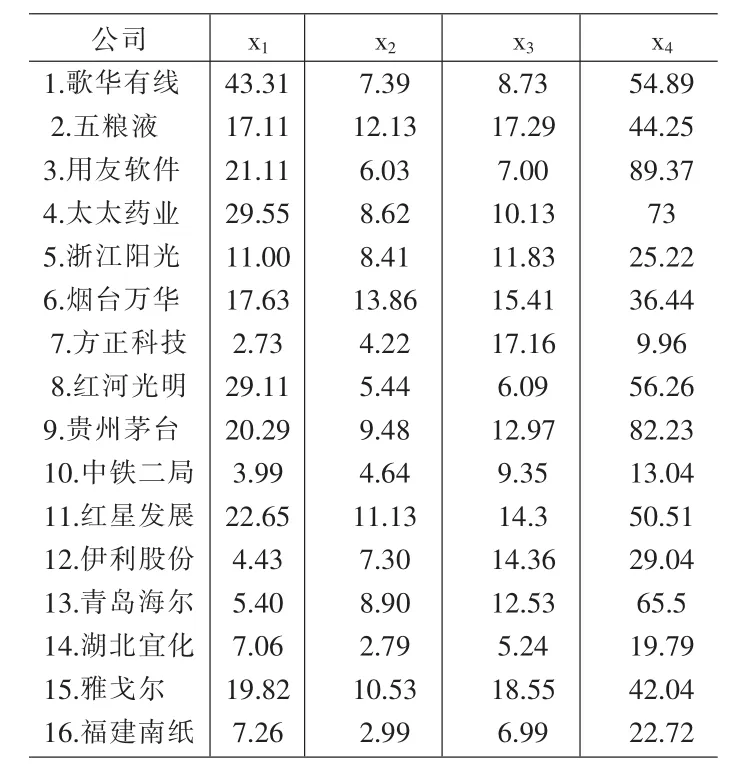
表7 上市公司赢利能力指标数据[9]

1.2 旋转后因子分析的综合评价步骤及其实例

旋转后因子分析的综合评价步骤。

⑴指标的正向化 (单独计算)[2]， 标准化；

⑵求变量的样本相关阵∑及其特征值λi，主成分法下初始因子载荷阵L0，旋转后因子载荷阵 LΓ(要计算出多个 LΓ)，旋转后方差贡献 qiΓ；

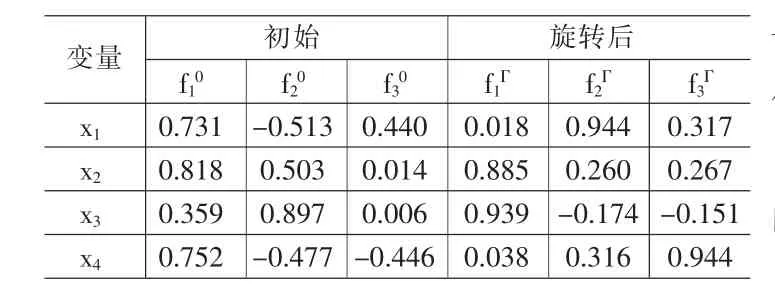
表8 因子载荷阵

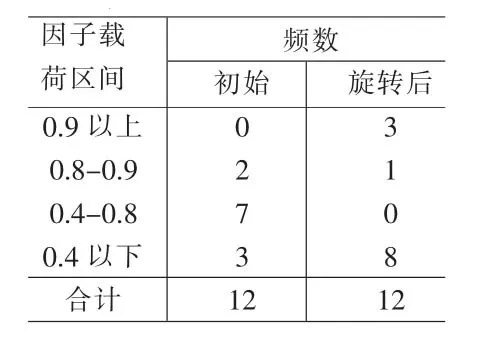
表9 因子载荷绝对值0、1两极分化频数对比表

⑶LΓ(要计算出多个 LΓ)与 L0比较，用因子载荷绝对值 0、1两极分化频数对比表判断(见表9)，如果LΓ中行元素绝对值足够向 0、1 两极分化，用旋转后因子 FΓ=(f1Γ,…,fmΓ)'进行分析[3]，继续[原始变量之间相关度很低或无关时，直接进行逐个指标分析，用∑i=1pXi作综合分析 (Xi是标准化的)是适合的]；

⑷确定旋转后因子个数m、因子方差累计贡献率：用LΓ和两变量显著相关的临界值判断，若因子与某些变量显著相关，则选入该因子[3]，因子个数m、因子方差累计贡献率随之确定；

⑸旋转后因子fiΓ的命名及其正向化：由LΓ的第i列fiΓ，将与fiΓ显著相关的变量归为fiΓ一类，由这些变量的意义对因子fiΓ进行命名(注意有些变量，可能与两个因子显著相关，命名中、分析中也要同时考虑好这些变量的联系性影响)。正向化[3]：如果这类变量与fiΓ的相关系数表明该类变量的意义是正向的，fiΓ不变符号；如果意义是反向的，fiΓ、liΓ同时乘上负号；

⑹计算写出旋转后因子 FΓ=Γ'(λ1-1/2a1'X,…,λm-1/2am'X)'(用LΓ回归的因子得分)；

⑺因为因子不相关，综合起来可反映样品的因子累加综合状况(不是反映多变量信息最大化时的样品值状况)，以旋转后因子方差贡献率qiΓ/p为权数得旋转后综合因子

⑻计算给出m个旋转后因子样品值矩阵HmΓ、旋转后综合因子样品值并排序；

⑼用m个旋转后因子样品值做聚类分析，按旋转后综合因子样品值排名顺序给出样品分类结果；[4]

⑽结合样品的分类结果，旋转后综合因子、其样品值和排序，原始数据，原始变量的意义，进行优势、劣势、潜力状况和影响因素等的综合评价，给出客观、可靠的决策相关性建议。

SPSS软件旋转后因子有关结果计算过程：原始数据的正向化数据输入或拷贝到数据窗口中，选择Analyze→Date Reduction→Factor→变量框中选入正向化的数据→Descriptives 选择 Initial solution,Coeffi-cients，Continue→Extraction选择 Principal Component，Correlation matrix(数据标准化被执行)，Number of factor：m，Unrotated factor solution，Screen Plot(碎石图),Continue→Rotation 选择 Varimax，Rotated solution，Continue→Scores 选 择 Save as Variables，Regression，Display factor score coefficient matrix，Continue→OK。计算结果有：样本相关系数阵R、R的特征值、旋转后因子的方差贡献、初始因子载荷阵、旋转后因子载荷阵、旋转后因子的标准化变量系数阵、旋转后因子的样品值数据等，数据窗口中的fac1-1,…,facm-1 为旋转后因子 f1Γ,…,fmΓ的样品值(注意 Extraction选择 Principal Component)。

例1.2 上市公司赢利能力的综合评价，指标体系选为：x1-销售净利率、x2-资产净利率、x3-净资产收益率、x4-销售毛利率，上市公司为青岛海尔、贵州茅台、五粮液等16家公司。数据见表6。

⑴表6数据全部是正向的；

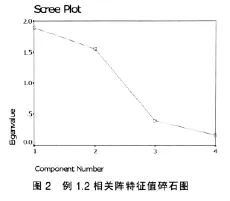
⑵调用SPSS软件因子分析主成分法下的过程命令，输入表6的数据，计算，经过挑选，m=3时，得初始因子、旋转后因子方差贡献表7，相关阵特征值碎石图图2，初始因子载荷阵L0、旋转后因子载荷阵 LΓ表8；

⑶由表8得表9，即旋转后因子载荷阵LΓ中行元素绝对值足够向0或1两极分化，故用旋转后因子解；

⑷前 3 个旋转后设为 f1Γ、f2Γ、f3Γ,变量正态分布下，取显著水平为5%，显著相关的临界值是r(14)=0.5[5]，由LΓ和显著相关的临界值 r(14)判断,因子 f1Γ、f2Γ、f3Γ与变量显著相关；其它因子与变量没有显著相关，故因子个数m=3，前三个因子解释X的信息(累计方差贡献率)为96%达到最大,误差因子解释变量X的信息为4%达到最小，结论可靠。

⑸因子命名与正向化：由LΓ和显著相关的临界值r(14)判断，f1Γ与x2-资产净利率、x3-净资产收益率显著正相关，因子f1Γ称为资产赢利因子；f2Γ与x1-销售净利率显著正相关，因子f2Γ称为销售净利率因子；f3Γ与x4-销售毛利率显著负相关， 因子 f3Γ称为销售毛利率因子。 因子 f1Γ、f2Γ、f3Γ是正向化的；

⑹用LΓ回归的因子得分函数(Xi是正向化、标准化的变量)：

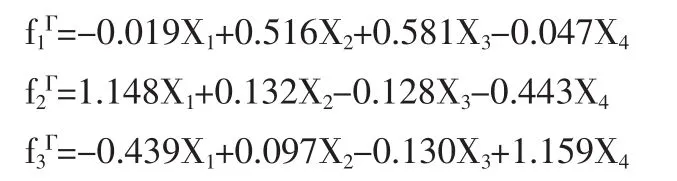
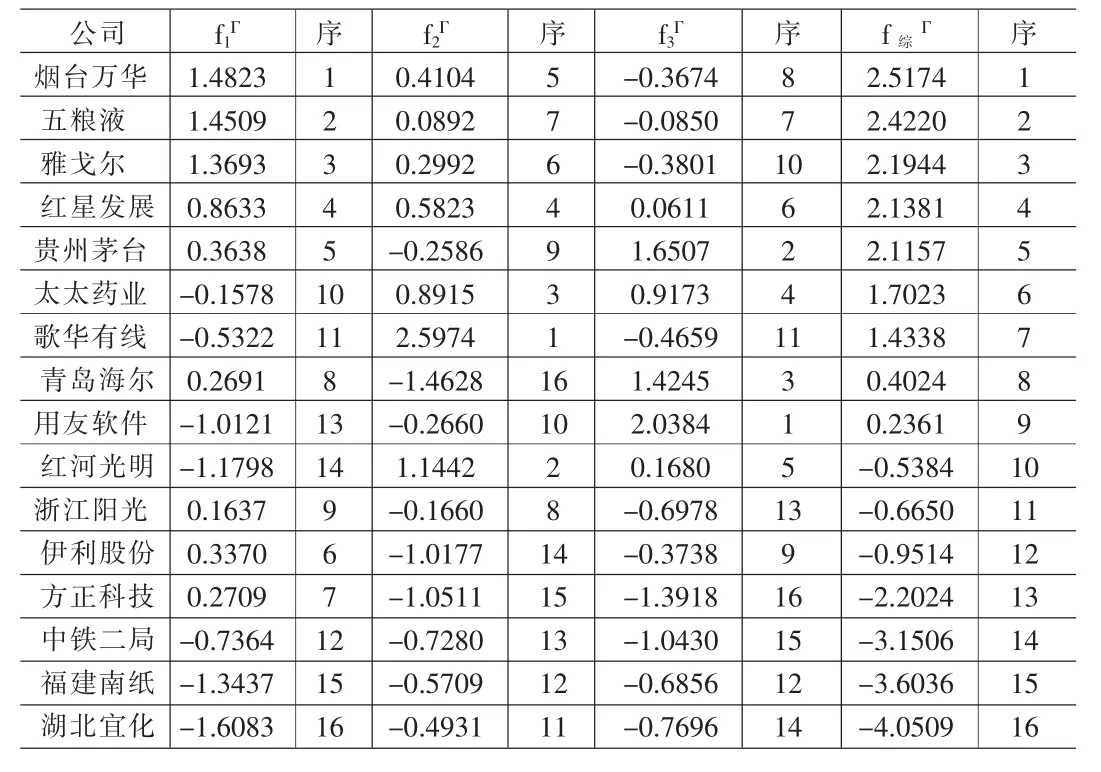
表10 旋转后因子、综合因子样品值

⑺以旋转后方差贡献率qiΓ/p为权数构造综合因子：

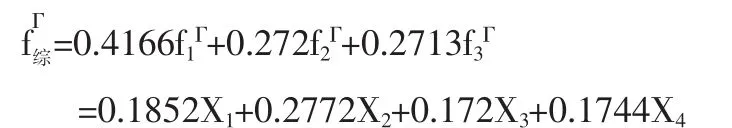
2X1-销售净利率(0.1852)，拉动的是X4-销售毛利率(0.1744)、X3-净资产收益率(0.172)。

⑻旋转后因子得分、综合因子样品值及排序见表10。

⑼调用SPSS软件的聚类分析类平均法过程命令，选用欧氏距离，通过旋转后因子得分 f1Γ、f2Γ、f3Γ的样品值对样品进行聚类。分成4类，结合综合因子得分样品值排名顺序给出相应共性分类结果如下：

第一类：烟台万华，五粮液，雅戈尔，红星发展；

第二类：贵州茅台，青岛海尔，用友软件；

第三类：太太药业，歌华有线，红河光明；

第四类：浙江阳光，伊利股份，方正科技，方正科技，中铁二局，福建南纸，湖北宜化；

⑽结合前3个旋转后因子得分样品值的聚类分析结果，因子得分、综合因子得分样品值和排序，因子得分、综合因子得分函数，原始数据，原始变量名称的意义，进行优势、劣势和影响因素等的综合评价，给出客观、可靠的决策相关性建议。

第一类的烟台万华、五粮液、雅戈尔、红星发展，综合因子得分值依次排第 1、2、3、4，全部高于平均水平。 其资产赢利因子f1Γ值依次排1、2、3、4,全部高于平均水平,优势明显。 销售净利率因子f2Γ值依次排5、7、6、4，全部高于平均水平，优势中上。 销售毛利率因子 f3Γ值依次排 8、7、10、6，其中红星发展、五粮液靠近平均水平，烟台万华、雅戈尔低于平均水平。即该类企业是综合赢利能力很强的企业，其中资产赢利能力尤其明显，销售净利率略高于平均水平，销售毛利率在平均水平附近的状况。建议：该类企业在继续保持资产赢利因子f1Γ中x2-资产净利率、x3-净资产收益率明显优势的情况下，销售净利率因子f2Γ中，应提高产品质量和管理水平，降低成本，进一步提高销售净利率的赢利能力；销售毛利率因子f3Γ中，销售毛利率提高的潜力较大，应向好的企业学习，改变销售毛利率赢利能力较差的状况。

第二～四类企业的综合评价、建议方法与第一类企业类似，此略。

以上1.1和1.2的分析及结论，找到了研究对象的共性、优势、不足、差距状况和原因等，用具有可控性的原始指标给出了可靠的决策相关性建议，验证了本文方法的有效性，且因子分析法的应用趋向深入。

1.3 旋转后因子解释原始数据的能力没有提高的实例

请见文献[6](2004)例6.1。

2 因子分析综合评价中的注意事项

⑴指标需要进行正向化、标准化，以便进行指标的相对比较。

⑵因子的明确：计算出多个旋转后因子载荷阵LΓ与初始因子载荷阵L0比较，用因子载荷绝对值0、1两极分化频数对比表判断，确定旋转后因子、初始因子哪个与变量相关性较高。

⑶确定因子个数m：用因子载荷阵和两变量显著相关的临界值判断，若因子与某些变量显著相关，则选入该因子，因子个数m、因子方差累计贡献率随之确定，这样不至于丢掉原始变量(初始因子个数、旋转后因子个数确定有时是不同的，如例1.2。设相关阵特征值碎石图拐点处的序号为k，旋转后因子个数m建议在k-1、k、k+1中挑选)。

⑷因子fi的正向化：由因子载荷阵的第i列li，将与因子fi显著相关的变量归为fi一类，如果这类变量与fi的相关系数表明该类变量的意义是正向的，fi不变符号；如果意义是反向的，fi、li同时乘上负号。这是因子进行综合的前提。

⑸使用旋转后因子时，因为旋转后因子方差贡献已发生改变，故旋转后综合因子以旋转后因子方差贡献率为qiΓ/p权数，即这样能保持方法的一致性。

⑹用前m个因子样品值做聚类分析，按旋转后综合因子样品值排名顺序给出样品分类结果，这样既有样品类的结果，又有样品序的结果。

⑺结合样品的分类结果，综合因子、因子样品值和排序，原始数据，原始变量的意义，进行优势、劣势、潜力状况和影响因素等的综合评价，尽可能给出客观、可靠的决策相关性建议。

[1]林海明.因子分析教学内容的改进—因子分析模型L的教学内容[J].统计与决策，2009,(23).

[2]林海明.对主成分分析法运用中十个问题的解析[J].统计与决策(理论版),2007，(8).

[3]林海明.因子分析模型的改进与应用[J].数理统计与管理，2009，(6).

[4]张尧庭,方开泰著.多元统计分析引论[M].北京：科学出版社，1982.

[5]峁诗松等编著.概率论与数理统计[M].北京：中国统计出版社，2000.

[6]何晓群编著.多元统计分析[M].北京:中国人民大学出版社，2004.