新兴市场股指期货价格发现功能的研究

方 斌

（天津大学 管理学院，天津 300072）

国内外对于股指期货推出后会对股票现货市场的波动性产生怎样的影响进行了大量的实证研究，由于各国的实际情况各不相同，所以至今并没有一致的结论。2000年6月，印度国家股票交易所（NSE）推出了其指数期货合约，NSE股指期货的合约标的为S&P CNX Nifty指数,自该期货合约推出以来，印度指数期货的交易量不断增加，虽然有时现货指数的波动性较大，但是期货交易所仍可保证市场的运作稳定、公平及有秩序。越来越多的投资者参与到S&P CNX Nifty指数交易中来，除了该指数本身所产生的吸引以外，更重要的原因是期货市场的运作符合国际标准。本文将利用计量经济学的方法对印度股指期货价格发现功能进行初步研究，这一研究对于中国即将推出的沪深300股指期货具有一定的借鉴作用。

1 实证方法

1.1 VAR模型

VAR是基于数据的统计性质建立模型，VAR模型把系统中每一个内生变量作为系统中所有内生变量的滞后值的函数来构造模型，从而将单变量自回归模型推广到由多元时间序列变量组成的“向量”自回归模型。VAR(p)模型的数学表达式是：

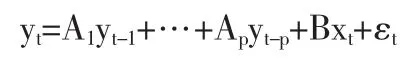
其中：yt是k维内生变量向量，xt是d维外生变量向量，p是滞后阶数。k×k维矩阵A1,…,Ap和k×d维矩阵B是要被估计的系数矩阵。εt是k维扰动向量，它们相互之间可以同期相关，但不与自己的滞后值相关及不与等式右边的变量相关。VAR模型常用于预测相互联系的时间序列系统及分析随机扰动对变量系统的动态冲击，从而解释各种经济冲击对经济变量形成的影响。

1.2 非线性因果检验

常见的Granger因果关系是对两个变量之间的线性因果关系做相应的检验，但是实际上两个变量之间的关系还包括非线性的作用，也就是说如果两个变量之间存在非线性的关系，那么两个变量之间也存在因果关系。如果两个变量x,y，存在下面的回归式：

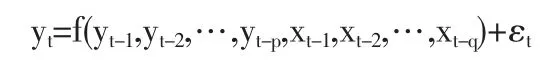
其中 εt～iid(0,σ)，{xt}，{yt}都是平稳的时间序列，函数 f代表两个序列之间的一种未知关系。因为在任意的样本空间，我们都能得到f的Taylor展开式，所以可以通过在样本空间中的任意一点对f做线性化展开。得到下面的式子：

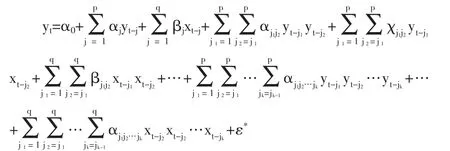
上面式子中包括了序列xt和yt滞后期的所有可能组合。对上面式子的回归，我们采用Lasso方法。对于一般的线性回归中，我们对变量的估计一般采用最小二乘法，Lasso方法是对最小二乘估计的一个推广，该方法的优势是它能使某些变量的参数快速收敛为零。实际上我们对变量做回归的时候也希望大多数变量的系数为零，并且系数不为零的那些变量对响应变量的影响尽可能的大，对于实际问题的解释也就更清楚明确一些。

2 数据说明

本文选取2002年8月14日至2005年12月9日印度S&P CNX Nifty股指现货和股指期货每日收盘价数据作为样本数据，因为这段时间是印度金融衍生品市场中相对成熟的阶段，具有较高的市场流动性。由于股指期货与现货市场不具有同时性，具有数据不连续的特点，同一交易日会同时有若干不同的交易价格，本文选取最近月份的期货合约作为代表，在最近期货合约交割后，选取下一个最近的期货合约为代表，将不匹配的数据删除，这样可以得到一个连续的期货合约序列，为防止分析过程中出现的异方差现象，以上数据均作对数处理。我们定义，CNS为S&P CNX Nifty现货指数对数序列，CNF为S&P CNX Nifty股指期货交易价格对数指数序列，数据来源于国泰君安证券研究所及yahoo财经网站，实证过程借助Eviews5.0软件和R软件。

3 实证分析

3.1 单位根检验

考虑到变量的非平稳性，避免模型中出现的伪回归的问题，我们在对变量进行协整分析之前首先利用ADF检验法对印度股指期货和现货的平稳性进行检验，若ADF检验值大于临界值，则时间序列为非平稳序列，反之则为平稳序列。对于非平稳序列，还需要检验其一阶差分序列的平稳性，若其t阶差分序列为I(0)序列（即平稳的时间序列），则此变量是t阶单整的。只有变量满足t阶单整的条件下，才能进行协整分析。本文通过CNS和CNF的时间趋势图的观察，可以判断出，CNF序列和CNS序列应选择含有截距项和具有时间趋势项的检验方程进行检验，而通过它们的一阶差分的时间序列趋势图的观察，可以判断出CNF序列和CNS序列的一阶差分应该选择具有截距项和没有时间趋势项的检验方程进行检验。具体检验结果如表1所示。

ADF的检验结果表明，在5%的显著水平下，CNF和CNS的序列存在单位根，是非平稳的时间序列，而它们的一节差分序列不存在单位根，是平稳的时间序列，因此可以判断所考察的时间序列都是1阶单整的。由于各序列均为同阶单整，下面我们就可以通过建立VAR模型进行协整关系检验。

3.2 协整检验

协整检验是从分析时间序列的非平稳性入手，寻找非平衡变量之间的长期均衡关系。常见的协整方法主要有两变量的Engle，Grenger检验（简称EG检验）和多变量之间的Johanson检验 （简称JJ检验）。EG检验是基于回归残差的检验，通过建立OLS模型来检验其残差的平稳性，若残差是没有单位根的平稳序列，则说明原序列存在协整关系。EG检验存在一定的缺陷，假如当协整关系的维数增加或协整的秩大于1时，EG检验便无能为力了。JJ检验是基于回归系数的检验，是利用向量自回归模型计算出与残差矩阵相关的矩阵的特征值，根据特征值的轨迹及最大特征值进行检验，该方法在一定程度上纠正了EG检验在多变量检验方面的不足。本文采用Johanson检验法来检验CNF和CNS之间是否存在长期稳定的均衡关系。

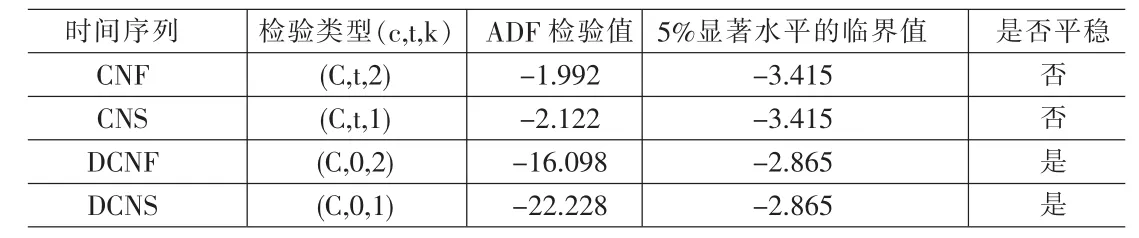
表1 ADF单位根检验结果

JJ检验的前提是建立VAR模型，建立VAR模型首先确定滞后期数k，若滞后期数k过大会导致自由度减小，直接影响模型参数估计量的有效性；若滞后期数k太小，则可能会导致误差项自相关问题，造成参数的非一致性估计。经过反复试验比较，滞后阶数为3时，AIC和SC值最小，同时本文选择有截距项但无确定趋势项的VAR模型来进行协整检验。检验结果如表2所示。

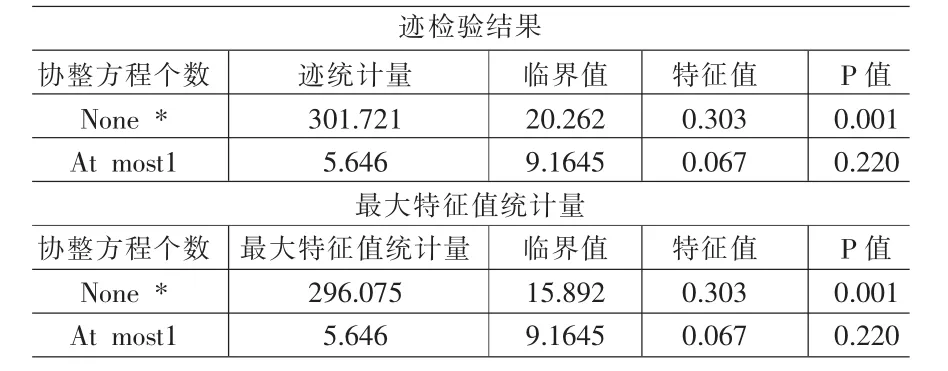
表2 Johensen协整检验

表2表示在5%的置信水平下，CNF和CNS之间仅有一个协整关系。协整系数可以标准化，在只考虑仅有一个协整关系的假定下，经过标准化的协整系数见表3。

表3给出了估计出的标准化的协整系数，由表3可以得到CNF与CNS之间的协整方程关系式：Z=CNF-1.007×CNS+0.054。然后对Z进行单位根检验，可以得出Z是一个平稳的时间序列。因此，从以上分析反映了CNF和CNS之间存在一种长期的均衡关系，且长期协整方程为CNF=1.007×CNS-0.054。

3.3 误差修正模型

误差修正模型（ECM）的优点是既可以克服对非平稳变量做回归时出现的伪回归问题，又可以同时考察变量间的短期和长期关系。当变量之间存在协整关系时，可以建立ECM来进一步考察短期关系。

根据表4中的误差修正模型1和模型2可知，模型1和模型2的误差修正系数分别为0.3393和-0.0057，并且二者在统计上都是显著的，说明当系统偏离均衡状态时，下一期期货价格和现货价格都将对非均衡状态进行修复。模型1中的误差修正项系数大于0，说明误差修正项对期货价格的变动具有正向调整作用。模型2中的误差修正项系数小于0，说明误差修正项对现货价格的变动具有负向调整作用。当短期价格偏离长期均衡状态时，股指期货将以33.93%的调整力度调整到新的均衡状态，而现货指数的调整力度仅为0.57%，因此期货市场在长期的价格发现过程中，相对占主导地位。

3.4 非线性因果关系检验

下面用Lasso方法，对印度股指期货和现货之间的非线性因果关系进行检验。做滞后期为2的非线性因果检验，首先做现货价格对期货价格的因果关系检验。用Lasso方法得出的结果如下所示：从1到10的变量分别如下：

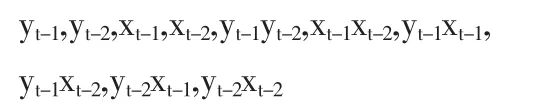
其中y代表期货价格，x代表现货价格。对于每一步计算的值如表5。

从Cp值可以看到在第5步的时候其值达到最小，则我们截取第5步的结果，这样分别选入的变量就有变量1(yt-1)，变量 8(yt-1,xt-2)，变量 4(xt-2)，变量 3(xt-1)以及变量 2(yt-2)。并且我们得到在第5步的时候其R2值为0.9907954，可见回归的效果是很好的。这样，我们就可以通过现货和期货的滞后一期和二期，以及现货和期货之间的交叉关系得出对期货的回归关系，也就说明了现货对期货具有非线性因果关系。

同样，我们可以做对现货价格的Lasso回归。从1到10的变量设置分别为：

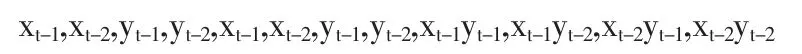
其中x代表现货价格，y代表期货价格。对于每一步计算的Cp值如表6。

从计算得出的Cp值可以看出，在第18的时候其值最小，所以我们截取18步的回归。而选入变量的结果可以通过上面Lasso的步骤过程得出，最后选入的变量为：变量1，变量2，变量 3，变量 4，变量 5，变量 6，变量 8和变量 9。同时也可以得到最后回归的R2值为0.9961607，可见回归效果还是比较满意的。这样可以得到期货同样是现货的非线性因果关系。

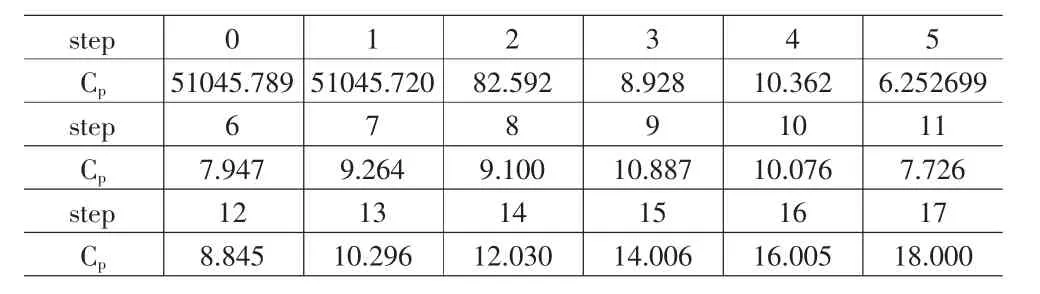
表5

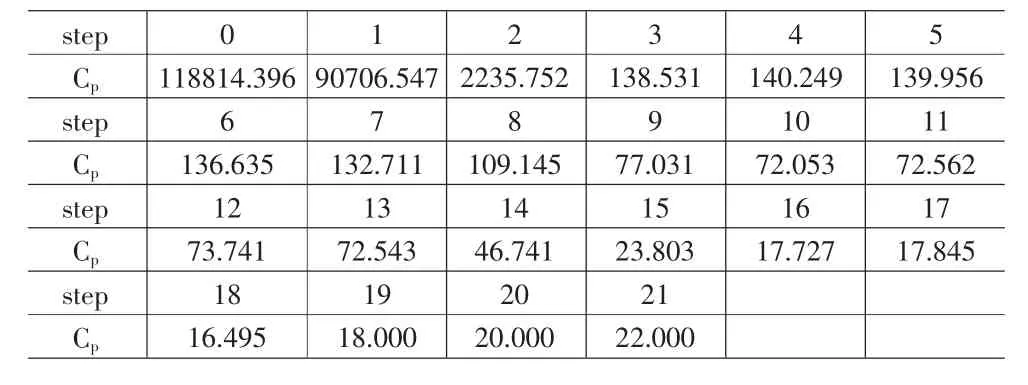
表6

4 结论

（1）VAR和协整检验的结果表明，短期内印度S&P CNX Nifty指数与期货指数之间可能出现偏差，但长期来说，印度现货指数与期货之间存在着长期稳定的相关关系，这种长期稳定的相关关系是对股指期货和现货的之间规律的一种定量的描述。

（2）通过VEC模型的检验，揭示了印度股指期货和现货之间从短期偏离到长期均衡的过程，DCNS模型中的误差修正系数相对较小，而DCNF模型中的误差修正系数相对较大，说明现货价格回复到均衡状态的速度相对较慢，即主要是通过期货价格的调整来完成，从而期货市场在价格发现功能中处于主导地位。

（3）从非线性因果关系的结果可以看出，现货价格对期货价格的因果关系中R2值为0.9907954，同样期货价格对现货价格的因果关系中R2值为0.9961607，说明二者相互拟合的效果都很好。也就是说印度S&P CNX Nifty指数和期货指数之间存在双向因果关系，即期货指数的变动影响到现货指数的变动，同时现货指数的变动也影响期货指数的变动，期货市场和现货市场之间的影响是相互的。

（4）印度指数期货成功的经验，可以为国内推出股指期货提供一些借鉴。一个金融期货产品的成功与否，取决于很多因素，其中稳定、成熟和高流通量的现货市场是发展股指期货的先决条件，也是股指期货市场发挥价格发现功能的基础，无论股指期货的推出还是风险的防范与监管都要考虑到现货市场的发展。

[1]陆樊祖.高等时间序列经济计量学[M].上海：上海人民出版社，1999.

[2]高铁梅.计量分析方法与建模[M].北京：清华大学出版社，2006.

[3]张晓峒.计量经济分析[M].北京：经济科学出版社，2006.

[4]Anne Peguin-Feissolle,Timo Terasvirta.A General Framework for Testing the General Noncausality Hypothese[C].SSE/EFI Working Paper Series in Economics and Finance,1999.