我国教育投资与经济增长的长期均衡与短期波动关系分析

郭新华，于骁玥

（湘潭大学 商学院，湖南 湘潭 411105）

0 引言

对于教育投资与经济增长之间关系的问题，综观目前已有的相关研究发现，国内外许多学者从不用的视角对教育投资进行过实证分析。总体看来，目前的研究主要存在三点不足：第一，有些学者在利用时间序列数据进行分析时，并没有对时间序列数据进行相应的处理或变换，而是直接拿没有按可比价进行折算的原始数据，进行最简单的最小二乘法估计，导致“伪回归”问题，由此得出的结论很可能是错误的。第二，在有的研究中，假定所使用的数据是平稳的。但实际上，很多经济数据具有时间趋势，要对数据进行平稳性检验及修正。否则，直接回归的结果可能不精确。第三，从目前的文献来看，大多数研究主要集中在教育投资与经济增长的长期关系，而缺乏对短期波动关系的研究。本文选取1991～2007年教育投资与经济增长的相关数据，分别从长期和短期探讨我国教育投资与经济增长的互动关系。

1 数据来源与研究方法

1.1 数据来源

在我国，教育投资来源是多方面、多渠道、多主体的，主要包括国家财政性教育经费，社会团体和公民个人办学经费，社会捐资和集资办学经费，事业收入及其他教育经费。其中国家财政性教育经费是我国教育经费的主要组成部分。鉴于数据的可获取性，因此选取样本区间为1991～2007年。选取国内生产总值（GDP，单位：亿元）作为衡量经济增长的指标。同时，选取国家财政性教育经费（Edu，单位：亿元）作为教育投资的代理变量。为了消除长期中价格变动对经济的影响，计量分析中使用的GDP值和教育经费都已经通过全国商品零售价格指数（PI）（以1991年为基期）转化为实际值。其中国内生产总值数据和1991～2006年的教育经费都来自《中国统计年鉴》（2008）的数据，2007年教育经费数据来源于2008年11月21日公布的《关于2007年全国教育经费执行情况统计公告》。由于对数据取对数不改变变量之间的协整关系，并且可以消除异方差，所以本文对变量做对数处理,记作LnGDP和LnEdu，相应的一阶差分序列记作ΔLnGDP和ΔLnEdu，二阶差分序列记作Δ2LnGDP和Δ2LnEdu。

1.2 长期协整关系检验方法

本文将建立时间序列模型，即用变量的过去值及随机扰动项所建立起来的模型。其一般形式为Yt=f(Yt-1，Yt-2，…，Xt-1，Xt-2，…，ut)。其中ut为随机扰动项（随机误差项），表示除X之外的其他影响Y的因素。平稳时间序列的特征是其均值和方差在时间过程上保持是常数，并且在任何两时期之间的协方差仅依赖于该两时期间的距离或滞后，而不依赖于计算这个协方差的实际时间。检查序列平稳性的标准方法是单位根检验，包括DF检验、ADF检验、PP检验、KPSS检验和ERS检验。比较常用的方法是ADF检验，这一检验是通过对非平稳序列的三种形式增加因变量Yt的滞后值，对其进行估计得到:

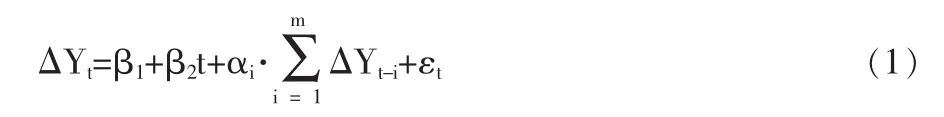
其中εt为纯粹白噪音误差项，原假设为：序列存在一个单位根（H0:γ=0）；备选假设为：不存在单位根序列（H1:γ=1）。通过最小二乘法得到γ的估计值构造检验＾显著性水平的t统计量，决定是否接受或拒绝原假设。

如果序列yt，通过d次差分成为一个平稳序列，而在d-1次时不平稳，那么序列yt为d阶单整序列，记为yt～I(d)。如果两个变量都是单整变量，并且单整阶数相同时，它们具有协整关系。协整的经济意义在于：两个变量虽然具有各自的长期波动规律，但如果它们是同阶协整的，则它们之间存在着一个长期稳定的比例关系。一般采用的是对残差进行单位根检验，如果残差序列平稳，说明回归方程中的k个变量之间存在协整关系。

1.3 短期波动分析方法

误差修正模型理论认为，由于我们使用的实际经济数据的生成过程存在非均衡。所以，需要用数据的动态非均衡关系来逼近经济理论的长期均衡过程。误差修正模型就是在协整关系的基础上，表示变量间的短期波动关系，该模型能够削弱原模型的多重共线性和扰动项的序列相关性。误差修正模型一般形式为：

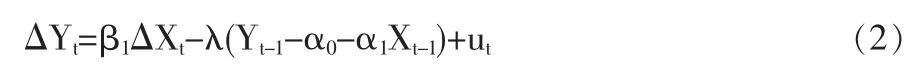
也可以表示为：

（2）式表明：Y的变化决定于X的变化以及前一时期的非均衡程度。同时，（2）式也弥补了简单差分模型ΔYt=αΔXt+vt的不足，因为该式含有用X、Y水平值表示的前期非均衡程度。因此，Y的值已对前期的非均衡程度作出了修正。其中，括号内的项就是 期的非均衡误差项。系数λ反映变量之间的均衡关系偏离t-1称其均衡状态时，将其调整到均衡状态的调整速度。

2 长期均衡分析

2.1 单位根检验

本文在分析变量之间的长期均衡关系前，为确保时间序列是平稳的，先对变量作单位根检验。使用计量经济分析软件Eviews5.0得出检验结果如下：

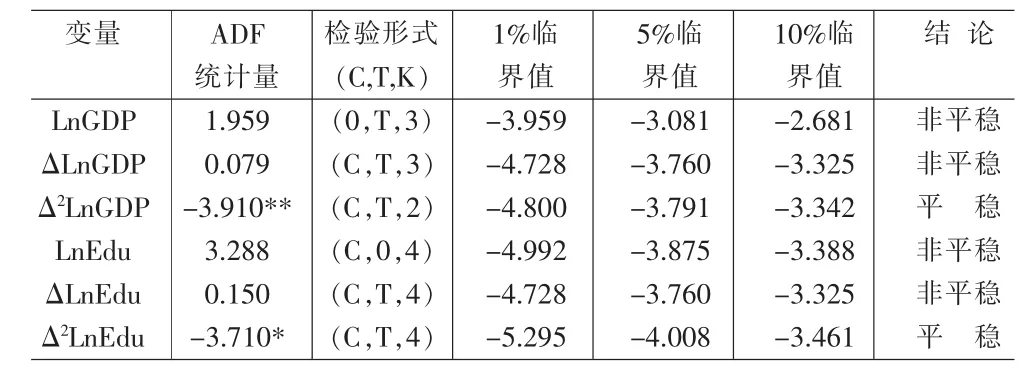
表1 变量序列的ADF检验结果

表1的检验结果显示，LnEdu序列和LnGDP序列以及其一阶差分序列都是非平稳的序列。但其二阶差分序列Δ2LnEdu在1%的显著性水平下拒绝原假设，接受不存在单位根的结论，即LnEdu～I(2)。二阶差分序列Δ2LnGDP在5%的显著性水平下拒绝原假设，接受不存在单位根的结论，即LnGDP～I(2)。说明这两个序列都是二阶单整，存在协整关系。

2.2 协整检验

根据协整理论，对于具有同阶单整的两个时间序列，可以通过判断其线性组合的残差是否平稳来判断两序列的协整性。如果残差检验结果是平稳的，就可以认为这二个序列之间存在协整关系。反之，则不具有协整关系。通过进一步对LnEdu序列和LnGDP序列做最小二乘回归得到：

方程中变量（含常数）下方圆括号中的数值为t检验值，说明相应的变量与Y线性相关的显著性；R2为拟合优度，DW为自相关检验，F值为F检验，SE为估计标准误差，它们是说明全部变量与Y线性相关性的显著程度。

从D.W.值来看，这个模型可能存在序列相关。但是，看起来不是很强。采用LM统计量进行检验（p=2）,得到结果如下（见表 2）：

表2

LM统计量显示，在5%的显著性水平拒绝原假设，回归方程的残差序列存在序列相关性。因此，回归方程的估计结果不再有效，必须采取相应的方法修正残差的自相关性。由于本文中的回归方程属于一元线性回归模型，修正其自相关性最常用的序列相关模型是P阶自回归AR(P)模型。修正后的结果为：

可以看出，修正后的回归方程的拟合度提高到了99.7%，D.W.值也提高了，通过LM检验得知，方程的残差序列的自相关性已经消除。因此，用AR（p）模型修正后的回归方程的估计结果是有效的。

为检验序列的平稳性，对（3）式的残差进行ADF检验，结果如下（见表3）：

检验结果显示，在95%的置信水平下，残差序列不存在单位根，即残差序列是平稳的。也就是说，我国教育投资与经济增长之间存在长期的协整关系。教育投资对经济增长的长期弹性为0.776，即教育投资增加1%，对经济增长的作用为0.776%。但由于常数项的存在（5.055），使得教育对经济增长的促进作用加大。

2.3 格兰杰因果检验

协整关系表明我国教育投资与经济增长之间存在长期均衡关系，但对于1991～2007年我国教育投资的发展与经济增长之间是否构成因果关系，还需要进一步进行格兰杰因果关系检验。由于格兰杰因果检验对滞后阶数非常敏感，经过多次试验，选取滞后阶数为2，利用Eviews5.0计量经济软件，检验结果如下(见表4)：

表4 时间序列△2LnEdu与△2LnGDP的格兰杰因果检验

由检验结果可知，F检验结果在5%的显著性水平下拒绝原假设。可以看出，我国教育投资是经济增长的格兰杰原因；而经济增长不是教育投资的格兰杰原因。

3 短期动态关系分析

以上的讨论主要是探讨LnEdu序列和LnGDP序列具有长期协整关系，为了得出LnEdu序列与LnGDP序列之间的短期波动关系，要建立误差修正模型来解释。利用Eviews5.0计量经济软件，得到的LnEdu序列和LnGDP序列的误差修正方程为：

ECM系数的大小反映了对偏离长期均衡的力度，误差项则反映了短期波动的影响。由方程(6)的系数估计值来看，误差修正项系数为负，符合反向修正机制。教育投资的短期变动可以分为短期经济波动的影响和偏离长期均衡的影响。从系数估计值（-0.375）来看，当短期波动偏离长期均衡时，将以37.5%的调整力度将非均衡状态拉回到均衡状态。由误差修正模型计算可以得到，LnEdu关于LnGDP的短期弹性为0.85。

同时，可以看到，教育投资滞后一期对经济增长的弹性系数为-0.104。得到这样的结论的原因是，由于我国教育投资对经济增长的贡献率低于世界平均水平，而且明显低于固定资产对经济增长的作用。所以，若加大对教育领域的投资，必然减少对其他领域的投资，原本的投资对经济增长的作用由教育投资所替代，短期内使经济增长降低。

4 结语

通过以上关于教育投资与经济增长关系的实证分析，可以得出以下结论：（1）在1991～2007年间，我国教育投资与经济增长既存在短期的动态关系，也存在长期的均衡关系。（2）格兰杰因果检验表明，教育投资与经济增长存在单向的因果关系，即教育投资是经济增长的原因，而经济增长不是教育投资的原因。（3）通过计量分析得出LnEdu关于LnGDP的长期弹性为0.766，短期弹性为0.85。（4）误差修正项表明，当短期波动偏离长期均衡时，将以37.5%的调整力度将非均衡状态拉回到均衡状态。这说明，教育投资与经济增长之间的均衡机制需加以完善。要发挥教育对经济增长的促进作用，政府应该：（1）加大对教育的投资，加快教育经费的增长速度。（2）优化教育经费结构，合理分担教育成本。（3）建立科学的经费管理机制，提高教育经费使用效率。

[1]Schultz,T.Investment in Human Capital[J].American Economic Review,1961,(51).

[2]David Alan Aschauer.Is Public Expenditure Productive[J].Journal of Monetary Economics，1989，(23).

[3]William Easterly,Sergio Rebelo.FiscalPolicy and Economic Growth:An Empirical Investigation[J].Journal of Monetary Economics,1993，32（3）.

[4]Micheal Brauninger,Jean-Pierre Vidal.Private Versus Public Financing of Education and Endogenous Growth[J].Journal of Population Economics,2000，(13).

[5]William F.Blankenau,Nicole B.Simpson.Public Education Expenditures and Growth[J].Journal of Development Economics，2004，(73).

[6]陈彬.用乘数模型估计高教规模扩大的经济影响应注意的问题[J].教育与经济，2000，（1）.

[7]李玲.中国教育投资对经济增长低贡献水平的成因分析[J].财经研究，2004，（8）.

[8]范柏乃，来雄翔.中国教育投资对经济增长贡献率研究[J].浙江大学学报（人文社会科学版），2005，（7）.

[9]栗建华，王其藩.基于系统动力学理论建模的教育投资、经济增长和就业问题的研究[J].科技导报，2007，（14）.

[10]周瓛.政府教育投入与经济增长相关性的实证分析[J].中国商界，2008，（7）.

[11]翁莉娟.我国教育投资与经济增长的协整分析与误差修正模型[J].数学的实践与认识，2008，（5）.

[12]饶华春.基于误差修正模型的教育投资于经济增长关系[J].现代管理科学，2008，（3）.

[13]达摩达尔·N·古扎拉蒂（美）.计量经济学基础[M].北京：中国人民大学出版社，2007.