开关磁阻电机RBF神经网络电流控制

孙鹤旭,李鹏,董砚

(河北工业大学 电气与自动化学院,天津 300130)

1 引言

开关磁阻电机(SRM)具有结构简单牢固、制作成本低廉、可控参数多、调速范围宽和系统效率高等优点。但是,电机本身固有的转矩脉动和非线性特性限制了其在工业领域的广泛应用。如何减小转矩脉动成了当前一个热门的课题。为减小SRM的转矩脉动,各国学者做了大量研究工作,提出很多方法,主要可以分为两大类:一是通过电机结构的优化设计来减小转矩脉动;二是通过控制算法来减小转矩脉动。文献[1]提出采用神经网络来优化开关磁阻电机的转矩。文献[2]提出给予RBF的神经网络对SRM的瞬时转矩进行控制。文献[3]采用迭代学习的方法减小SRM的转矩脉动。

然而由于开关磁阻电机按照“磁路最小”的工作原理设计,其电感是转子位置的非线性函数,开关磁阻电机两相励磁运行时,由于存在互感影响,其电感模型更加复杂。文献[4]中提到了采用磁网络模型对开关磁阻电机两相励磁运行时的磁场特性进行分析,为开关磁阻电机两相励磁运行时电流控制分析提供了很好的理论方法。

本文从电磁的角度对开关磁阻电机定子绕组电感进行分析,基于RBF神经网络建立了SRM的电感非线性模型,RBF网络为3-6-1结构(3个输入变量、6个隐层节点、1个输出量)。最后通过离线训练完成SRM在两相励磁时考虑互感的电感与转子位置的非线性建模,使该模型能有效映射电感与转子位置和定子电流之间的非线性关系。最后通过已建立的电感模型动态调节PWM的占空比,使实际电流很好地跟随给定电流,并经过实验验证该方法能获得满意的电流控制效果。

2 电机励磁电感分析

8/6结构的开关磁阻电机采用图1所示的电容分裂式功率拓扑结构,其各相绕组电流可独立控制,从而降低转矩脉动,提高开关磁阻电机的性能。但在实际控制中发现,相电流控制存在一定难度,开关磁阻电机是按照“磁路最小”的工作原理设计的,因此当给定子绕组通以电流时,产生的磁链不仅与电流有关,还与转子位置有关。在不同的转子位置,电感是不一样的,同样占空比的PWM作用下,电流的变化值是不一样的。

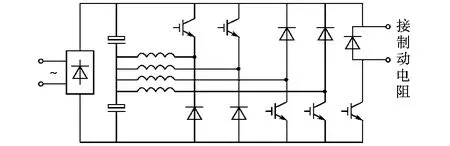
图1 SRM功率拓扑结构图Fig.1 Power topology of SRM

从电磁角度分析,开关磁阻电机各相绕组均绕在定子上,转子的位置决定磁场的分布。图2是8/6结构开关磁阻电机两相同时激励时(两相绕组都施加6 A电流)的磁场分布图。一相处于齿齿对齐位置,另一相处与齿齿相差15°位置,两相定子绕组均施加6A电流。

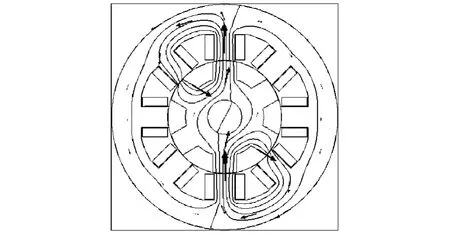
图2 SRM两相励磁的磁场分布图Fig.2 Magnetic distribution of SRM 2-phase excitation

对于8/6结构开关磁阻电机,磁链和电感可以用下式表示:

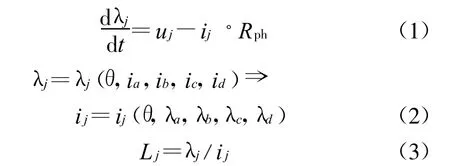
式中:λj为j相绕组产生的磁链;uj为j相绕组两端的电压;Rph为绕组电阻;Lj为j相绕组电感。

当两相同时导通时,以 A,B相导通为例,A相磁链可用2部分表示:

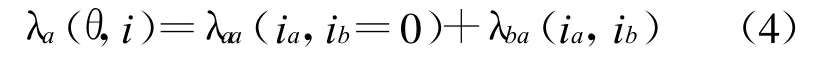
SRM的电感包括自感和互感2部分,由式(3)可得

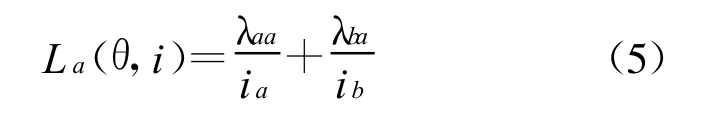
3 RBF神经网络

由上面分析可知,SRM电感是与转子位置相关的非线性函数,显然传统的性能分析方法不能解决这个问题。

人工神经网络具有很强的非线性映射功能,在控制中,应用较多的网络是BP网络,但BP网络采用的是一阶梯度下降法来学习的,故存在局部极小值,速度也比较慢(耗时太长)。RBF网络具有最佳逼近的特性,收敛速度快,在一定程度上克服了这些问题[5,6],近年来,RBF神经网络在非线性系统建模和控制等方面得到广泛的研究和应用。

图3给出的是一个多输入、多输出的RBF神经网络结构图。图3中,RBF网络有2层组成:输入层实现从x到aj(x)的非线性映射;输出层实现从aj(x)到y的线性映射。常用的 RBF基函数是高斯基函数。

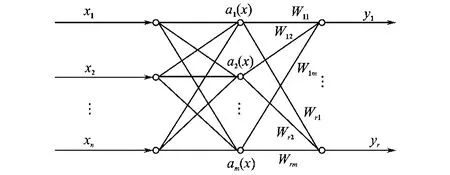
图3 RBF神经网络结构图Fig.3 The neural network of RBF

本文采用RBF网络对SRM电感进行非线性建模。SRM的电感包括自感和互感2部分,而且与转子位置相关,因此以 A相电感为例,将转子位置θ,自身电流ia及同时导通的另一相邻相电流ineighbor作为神经元的输入,即

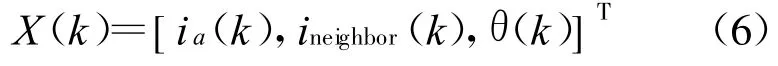
对于隐层径向基函数采用高斯核函数

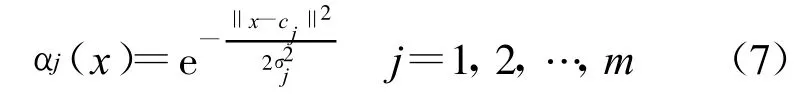
式中:αj为第j个隐层单元的输出;‖*‖为欧几里德范数;x为RBF网络的输入;cj为第j个隐层节点的中心;σj为第j个隐层节点的宽度。

电感作为RBF网络的输出

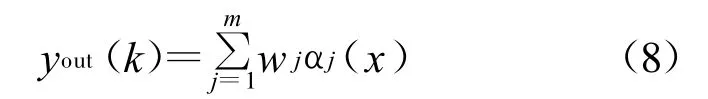
式中:wj为第j个隐层节点的连接权。

隐层节点数量的确定要考虑到系统的实时性要求。在既满足一定网络期望精度的要求又要满足控制实时性要求的情况下,隐层节点数确定为6个。即整体RBF网络为3-6-1结构。最后通过离线训练完成SRM在两相励磁时考虑互感的电感与转子位置的非线性建模。

为确定输出权值、隐层中心及基宽参数,定义二次性能指标函数为

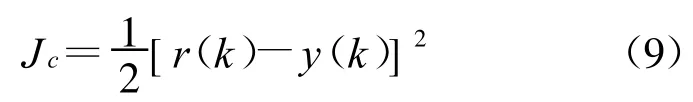
式中:r(k)为系统参考输入;y(k)为系统输出。

则可由梯度下降法得到输出权值、隐层中心及基宽参数的更新算法如下:

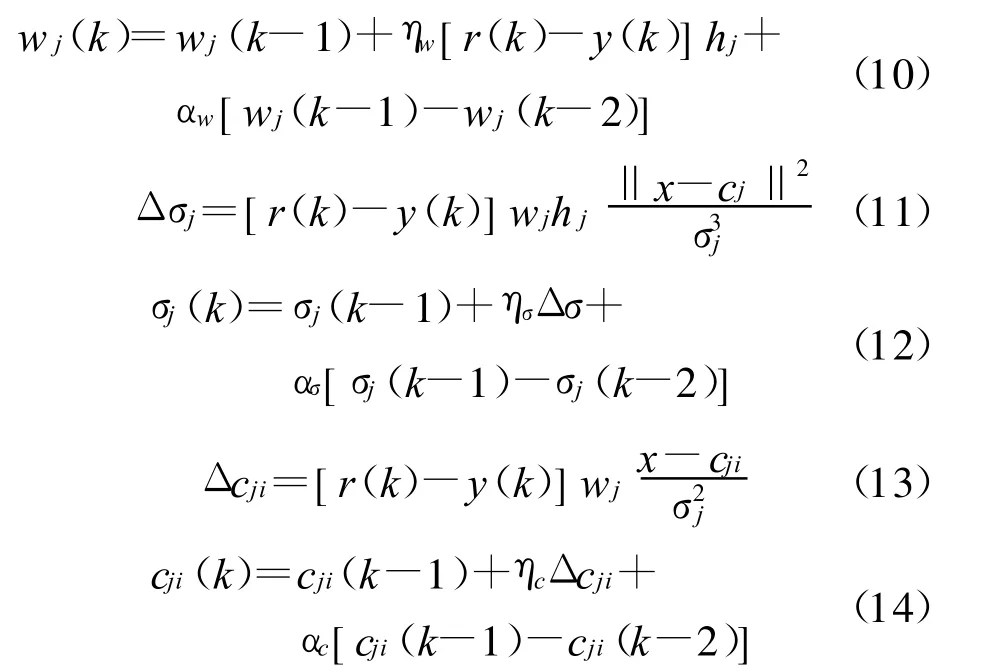
式中:j=1,2,3,4,5,6;i=1,2,3;ηw,ησ,ηc 分别为输出权值、基宽及隐层中心的学习速率;αw,ασ,αc分别为它们的动量因子。

4 实验结果

本文以TI公司的数字信号处理器TMS320LF2407为核心控制芯片,验证所提出的控制方法的性能。控制系统框图如图4所示,与传统PWM控制相比,系统增加了RBF网络,考虑到绕组电感对电流变化的影响。基于RBF网络的SRM电感模型建立起来以后,在转子的不同位置,根据RBF网络得到的电感值实时调节PWM的占空比。RBF网络通过离线训练得到,控制算法通过DSP由软件实现。

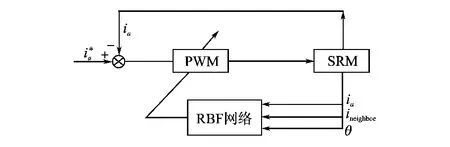
图4 SRM电流控制系统框图Fig.4 SRM current control system framework

功率电路采用电容分裂式拓扑结构,主开关器件采用IGBT。实验选用1台8/6结构开关磁阻电机,额定功率 0.75 kW,额定转速 1 500 r/min,Lmin=13 mH,Lmax=270 mH。

图5、图6均为给定电流为2 A,在不同电压等级下,传统电流PWM控制和采用RBF网络对电流PWM控制进行改进的对比电流波形。

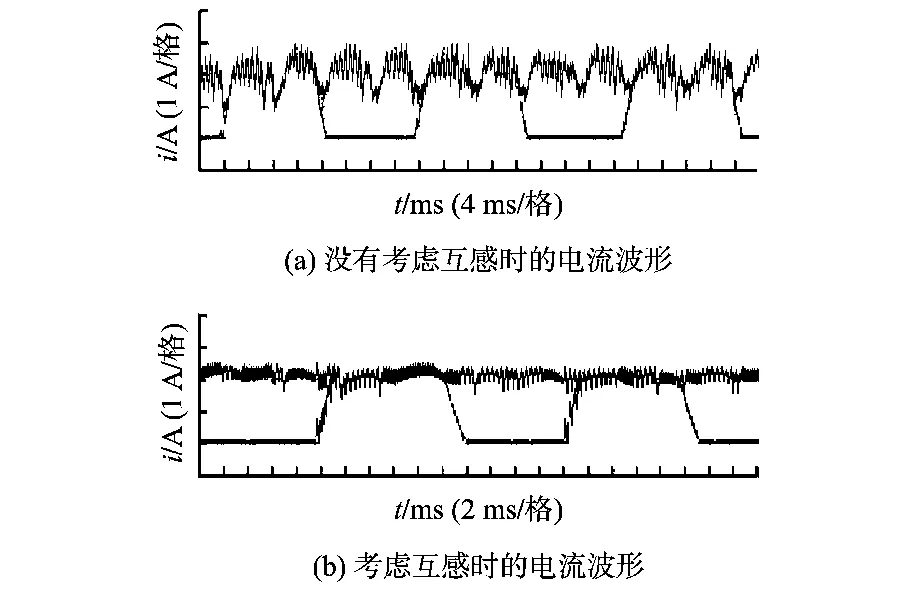
图5 有无考虑互感时的电流波形对比(给定电流2 A,Us=155 V)Fig.5 Current waves compare with&without mutualinductor(given current 2 A,Us=155 V)

图5为给定电流2 A,电压155 V时传统电流PWM控制和采用 RBF网络对电流PWM控制进行改进的电流波形。如图5a所示,传统电流PWM控制下,在不同转子位置由于电流变化率不一致,导致电流波动很大,波动为±1 A。图5b为采用RBF网络对传统电流PWM控制进行改进的电流波形,波动为±0.4 A,通过这种办法使电流波动大大减小,提高电流控制精度。

图6为给定电流2 A,电压310 V时传统电流PWM控制和采用 RBF网络对电流PWM控制进行改进的电流波形。如图6a所示,传统电流PWM控制下,波动为±2 A。图6b为采用RBF网络对传统电流PWM控制进行改进的电流波形,波动为±1.4 A。这是因为电源电压变大,导致在一个斩波周期中绕组电流变化相应变大。因而图6的电流波形波动比图5大。

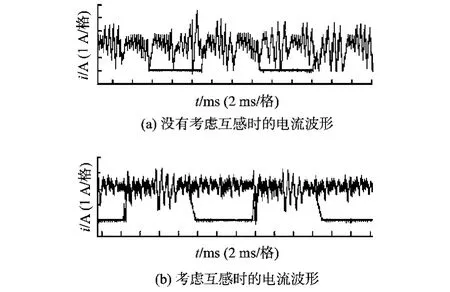
图6 有无考虑互感时的电流波形对比(给定电流2 A,Us=310 V)Fig.6 Current waves compare with&without mutualinductor(given current 2 A,Us=310 V)

图5、图6说明采用该方法在不同电压给定下都能在很大程度上平滑电流波形,获得满意的实际控制效果。

5 结论

开关磁阻电机的转矩与电流和电感直接相关,只有控制好电流,才能获得理想的转矩。SRM电感模型存在严重的非线性,难以精确建立。而RBF网络特别适合于非线性对象建模,同时具有最佳逼近及收敛速度快的特性,在满足控制要求的情况下,选择合适的隐层节点数目,能满足控制的实时性要求。本文依据RBF网络对SRM电感进行建模,根据不同转子位置的电感值动态调整PWM的占空比,改善了对电流的控制效果。

[1]Zhengyu Lin,Donald S Reay,Barry W Williams,et al.Torque Ripple Reduction in Switched Reluctance Motor Drives Using B-spline Neural Networks[J].IEEE Trans.Ind.Appl.,2006,42(6):1445-1453.

[2]Sahoo N C,Xu J X,Panda S K.Low Torque Ripple Control of Switched Reluctance Motors Using Iterative Learning[J].IEEE T ransactions on Energy Conversion,2001,16(4):318-326.

[3]王宏华.开关型磁阻电动机调速控制技术[M].北京:机械工业出版社,1995.

[4]郭伟,赵争鸣,詹琼华.磁网络模型在两相激磁开关磁阻电机中的应用[J].中国电机工程学报,2006,10(2):154-159.

[5]夏长亮,王明超.基于RBF神经网络的开关磁阻电机单神经元PID控制[J].中国电机工程学报,2005,25(15):161-165.

[6]王旭东,邵惠鹤.RBF神经元网络在非线性系统建模中的应用[J].控制理论与应用,1997,14(1):59-66.

[7]Amit Kumar Jain,Ned Mohan.Dynamic Modeling,Experimental Characterization,and Verification for SRM Operation with Simultaneous Two-phase Excitation[J].IEEE Transactions on Industrial Electronics,2006,53(4):1238-1249.

[8]ZHENG Yi,SUN He-xu,DONG Yan,et al.Torque Ripple Minimization with Current Oriented Method for Switched Reluctance Motor[C]∥ICEMS2007.

[9]O′Donovan J G,Roche P J,Kavanagh R C,et al.Neural Network Based Torque Ripple Minimization in a Switched Reluctance Motor[C]∥in Proc.IECON,1994:1226-1231.

[10]Husain I,Ehsani M.Torque Ripple Minimization in Switched Reluctance Motor Drives by PWM Current Control[J].IEEE Trans.Power Electron,1996,11(1):83-88.