让学生亲历定理的发现过程

✿青海省格尔木市万化中学 秦万明

“数学课程标准”在关于课程目标的阐述中，大量使用了“经历（感受）、体验（体会）、探索”等刻画数学活动的过程性动词.具体而言，就是在数学学习的过程中，要让学生经历知识与技能形成的过程，经历数学思维的发展过程，经历应用数学能力解决问题的过程，从而形成积极的数学情感与态度.本文就数学课堂教学中如何设计教学方案让学生亲历定理的发现过程，举例说明.

三角形内角和定理的教学

有不少教师已注意到突出定理结论的发现过程的重要性，利用剪拼方法，归纳得出三角形内角和为180°的结论.但是很少注意到暴露定理被发现的过程，而这正是一个重要的思维环节.为此，我设计如下教学方案.

1.如图l，a//b，它们被c所截得的同旁内角和∠1+∠2=？

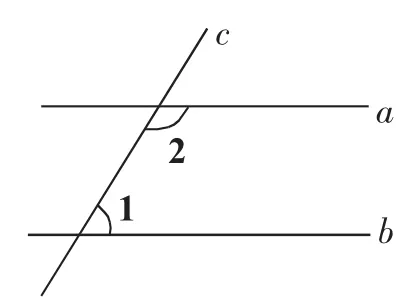
图l

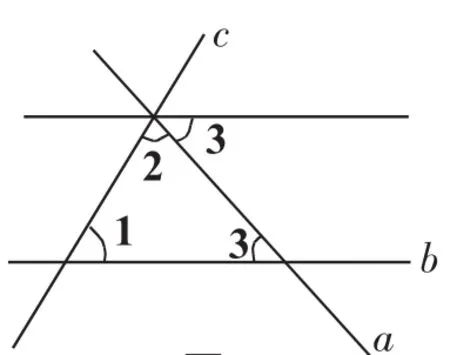
图2

2.若a与b相交，如图2，∠l+∠2仍然等于180°吗？发生了什么变化？减少了多少？∠3跑到哪里去了？可以得到什么结论呢？

这样的教学设计，暴露了“三角形内角和”与“平行线性质定理”的关系，突出了它们的内在联系.

圆周角定理的教学

教材通过由特殊到一般的程序，突出了定理的证明方法.但仍然没有暴露概念形成与定理发现的过程.因此，可设计如下教学方案.

1.提供问题的背景.

如图3，∠AOB为⊙O的圆心角，∠AOB如何度量？

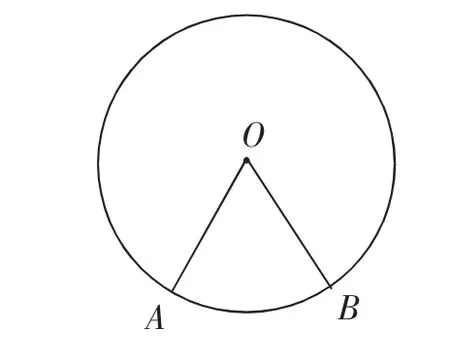
图3

2.提出问题一般化.

若∠AOB的顶点不在圆心，而是圆内任意一点P，∠APB如何度量？如图4.

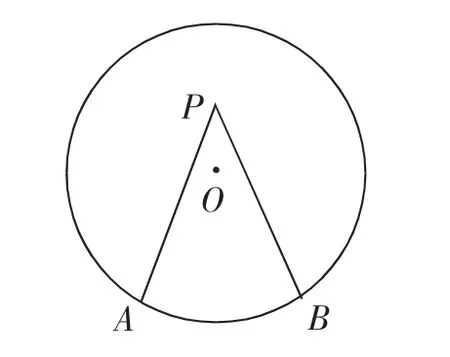
图4

引导学生比较图3中的∠AOB与图4中的∠APB，特别在∠AOB的两边都通过圆心.那么，O在AP边上，则∠APB如何度量？如图5.

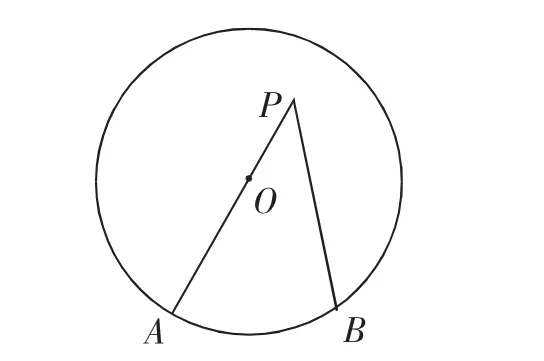
图5

3.特殊化思考.

当P在AO上运动时，∠APB仍然不是定值，能否考虑更特殊的情况，比如P在圆周上（直径的端点）时，不难得到∠APB=∠AOB，如图6.

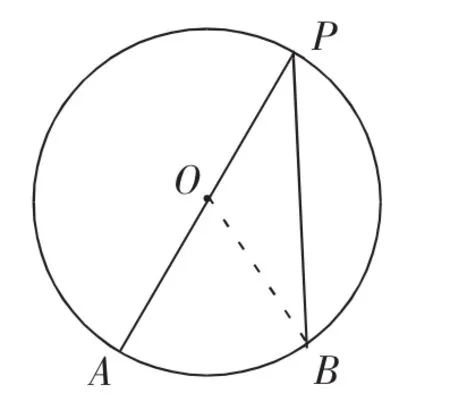
图6

若圆心O不在角的任何一边，又有什么结论呢？如图7和图8.

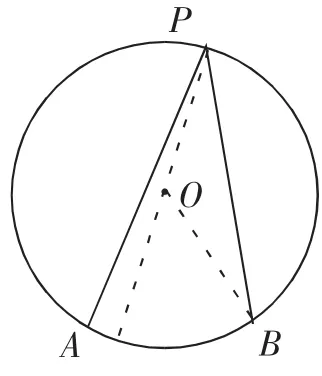
图7

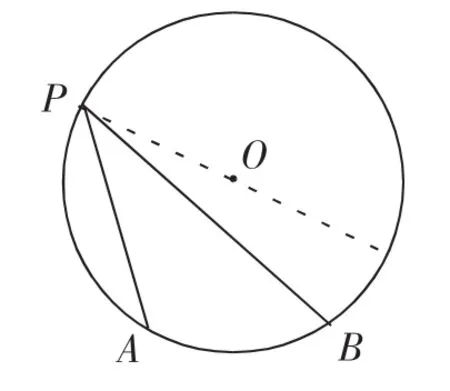
图8

你能否化归为已经解决的图6的问题.

这样我们发现了圆周角的度量方法，给出圆周角定理.如上教学设计，揭示了圆心角、圆周角的内在联系，既突出了知识结构，又强调了化归的基本思想方法.

平行线分线段成比例定理及其推论的教学

用运动变化的观点阐述几何定理，可借助教具通过演示，揭示知识的发生、发展过程，使学生对定理的形成过程有一个完整的认识.例如“平行线分线段成比例定理”及其推论，可以借助教具演示，用运动变化的观点加以分析，使学生看到数学知识不再是零碎的、孤立的、静止的内容，而是一个活生生的整体.

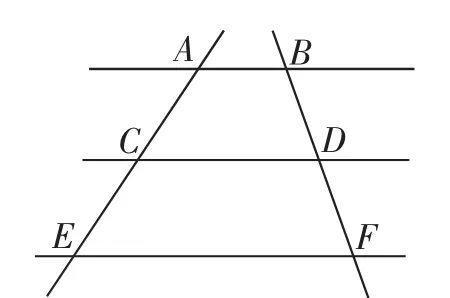
图9

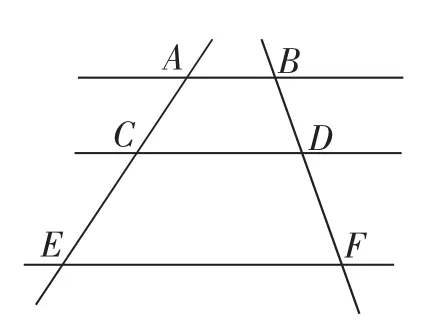
图10

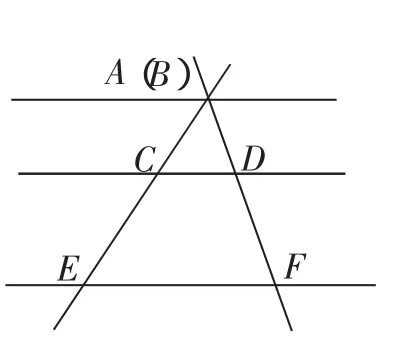
图11

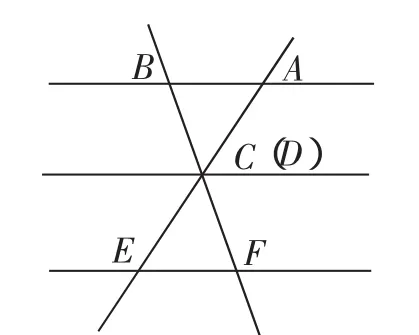
图12

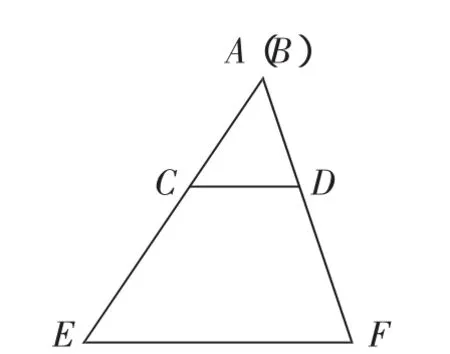
图13

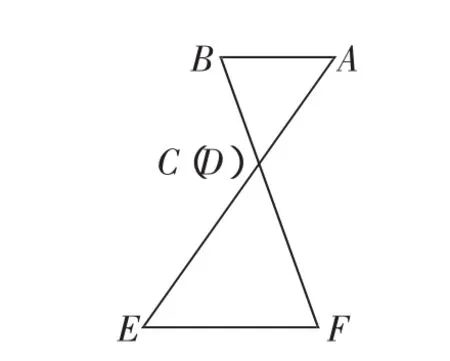
图14

从图9可以清楚地看到，把CD向上运动，即得图10.把AE逐渐向右运动，即得图11与图12.而把图11与图12中的直线看作线段，即是图13与图14.这样，由平行线等分线段定理到平行线分线段成比例定理及其推论间的相互联系，也就跃然而出.

这里用运动的观点暴露了由特殊到一般的认识过程，又让学生体会到“新→旧→新”的转化过程.

实践表明，学生充分经历学习过程，思维高度集中，参与教学过程，摆脱被动接受知识的心理状态，变“苦学”为“乐学”.从教育学的角度看，在教师的启发下学习，使教与学有机结合，学生的主体地位得到了加强，使学得的知识更加扎实，分析解决问题的能力也相应地提高，从而大面积提高教学质量.