谈判定常见图形对称性的规律

✿哈尔滨市第69中学 刘洋

对称图形是一个具有特殊形状的图形，他具有结构美观、匀称、旋转稳定等特殊性质，在实际生活中有着广泛应用.判定图形的对称非常适于考查学生观察猜想、动手操作、推理判断的能力.因此，考查图形（或图案）的对称性问题备受中考青睐.本文就判定初中几何图形（或图案）的对称作一探讨.

一、轴对称图形的判定

轴对称图形是关于直线对称的图形，它具备下列基本性质：

1.图形沿对称轴对折后，图像上的任意一个点关于对称轴存在另一个点与之唯一对应（对称点）.特别当图形上某一个点处在对称轴上时，其对称点就是它自身；

2.对称轴垂直平分不在对称轴上的对称点所连成的线段.

轴对称图形中基本的对称图形是角与线段.角只有一个顶点（奇数），角的平分线是对称轴，显然对称轴平分处在对称轴上的定点所在位置的内角.线段有两个端（顶）点（偶数），线段的垂直平分线是其中一条对称轴，显然对称轴垂直平分不在对称轴上的对称点所连成的线段.

轴对称图形的判定有下列一般规律：

1.图形的顶点个数是奇数.

（1）图形只有一个顶点时，同时平分一组从顶点出发的两条直线所构成的夹角（夹角为180°时两条直线在同一条直线上）的直线（如图1）.

（2）图形中若存在一个内角（至少）的角平分线垂直平分某一条边，同时在此角平分线一旁的其余各点总能在该直线另一旁找到一个点，使得这两个点所连成的线段被该直线垂直平分，此直线一定是对称轴（如图2）.

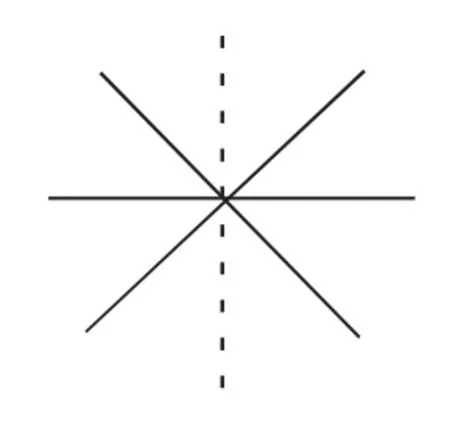
图1

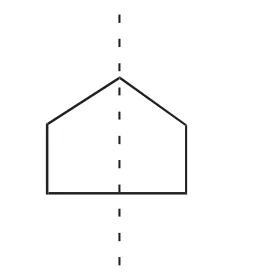
图2

2.图形的顶点个数是偶数.

（1）如星中若存在一条边垂直平分线垂直平分另一条边，在此垂直平分线一旁的其余各点总能在该直线另一旁找到一个点，使得这两个点所连成的线段被该直线垂直平分，此直线一定是对称轴（如图3）.

（2）图形中若存在一个内角（至少）的角平分线平分另一个内角，同时在该直线一旁的其余各顶点总能在该直线另一旁找到一个点，使得这两个点所连成的线段被该直线垂直平分，此直线一定是对称轴（如图4）.

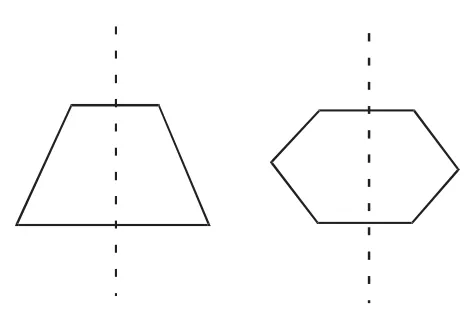
图3

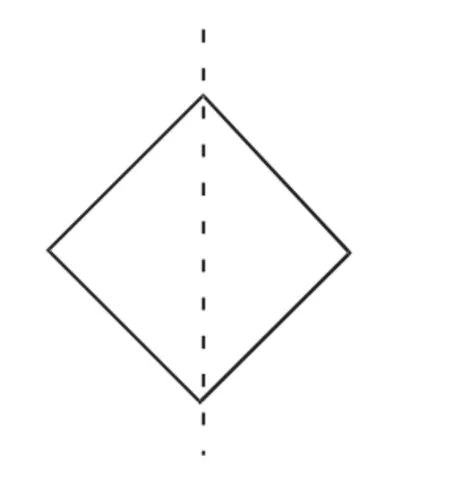
图4

二、中心对称图形的判定

中心对称图形是关于点对称的图形，它具备下列基本性质：

1.图形上的任意一个点关于对称中心旋转180°后所到达的位置，原图形总存在一个点与之唯一对应（对称点）；

2.图形上的任意一个点不与对称中心重合，图形的任意一个点不能构成自对称；

3.对称中心平分经过对称中心的图形的对角线（对角线即对称点所连成的线段）.

中心对称图像中最基本的对称图形是线段，线段有两个端（顶）点（偶数），对称中心是线段的中点.

判定中心对称图形有下列一般规律：

1.图形的顶点个数是偶数；

2.连接图形上各个顶点的所有对角线中，对角线同时经过一点，且被此点平分，此点一定是对称中心.

特别地，相交直线的焦点不能看作图形的顶点.其顶点是除交点以外的直线上的点.交点是对称中心（如图5、6）.

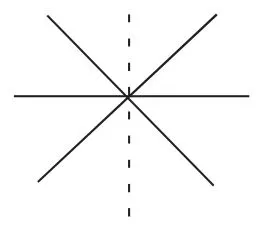
图5

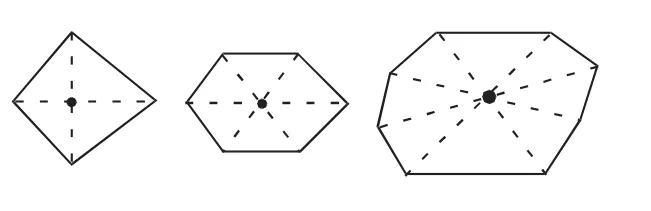
图6

三、同是轴、中心对称图形的判定

这类图形既是关于直线对称、又是关于点对称的图形，它必须同时具备轴对称、中心对称图形的性质.因此，其判定有下列一般规律：

1.图形的顶点个数是偶数.

2.图形是至少存在两条互相处置的对称轴的轴对称图形.

3.图形是对角线平分且过对称轴交点的中心对称图形.这样的图形一定既是轴对称又是中心对称图形（如图7）.

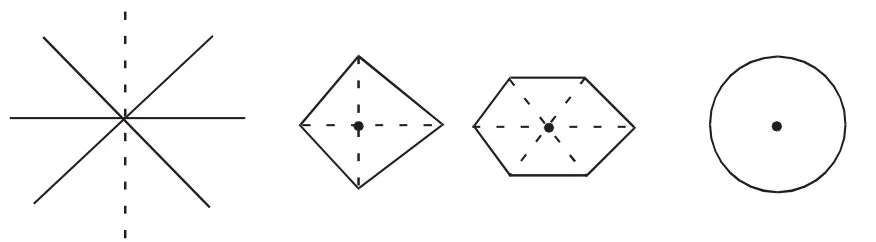
图7

四、图案对称性图形的判定

图案是由“基本图形或基本图案”通过平移、旋转、轴对称以及组合而构成，这种变化的图案形式多样.轴对称图案，中心对称图案，同时轴、中心对称图案，是对称图案的3种基本特征：

1.“基本图形与图案”是轴对称图形.

2.“基本图形与图案”是中心对称图形.

3.“基本图形与图案”同是轴、中心对称图形.

因此，对称图案的判定有下列一般规律：

1.轴对称图案（1）任意图形直接运用轴对称形成的图案.（2）基本图形的平移方向垂直于“基本图形”的对称轴、沿“基本图形”的对称轴上下平移、沿“基本图形”的对称轴两侧与对称轴成等角平移且距离相等形成图案（如图8）.（3）对“基本图形”旋转任意角度后形成的图案（如图9）.仍符合轴对称图形的判定规律.

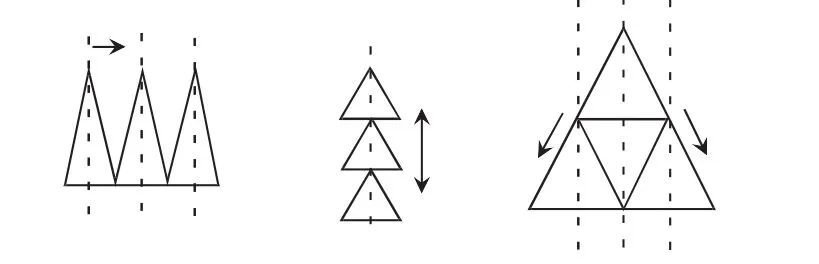
图8

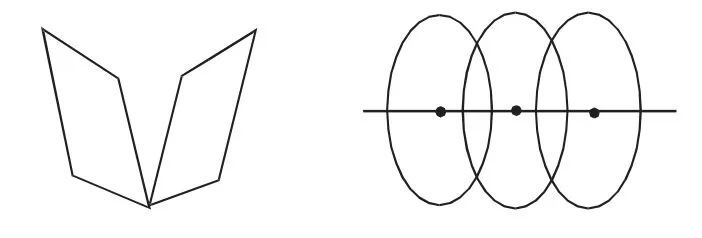
图9

2.中心对称图案（1）基本图形平移后，“基本图形”的对称中心共线或连接“基本图形”对称中心的图形是中心对称图形的图案（如图10、11）.（2）直接以“基本图形”的对称中心旋转任意角度后形成的图案（如图12）.（3）运用轴对称形成的图案（图略）.人符合中心对称图形的判定规律.

3.同是轴、中心对称图案：图案符合轴对称、中心对称图案的判定规律（如图11、12）.

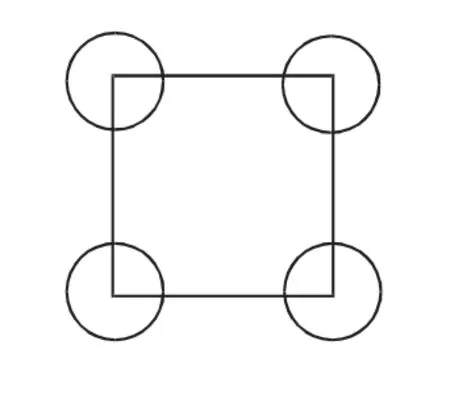
图11

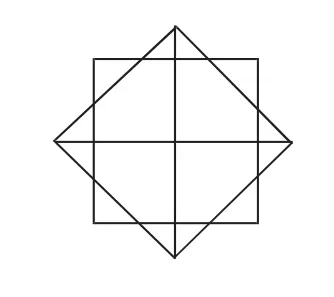
图12

综上所述，判定图形或图案的对称是有规律可循的.掌握了图形或图案对称的一般规律，学生不仅能够解决图形或图案的对称性问题，而且有利于学生利用图形或图案的对称规律解决其他实际问题.