高考中的不等式恒成立问题与走势
2010-06-08台州市第一中学浙江台州318000
● (台州市第一中学 浙江台州 318000)
1 考点回顾
不等式恒成立问题常以函数、方程、不等式和数列等知识点为载体,考查等价转化、分类讨论、数形结合、函数和方程等数学思想方法.此类问题既体现了考题的综合性,又考查了学生的综合分析能力,因此它已成为各地高考的一大热点.2007年和2008年考题中的不等式恒成立问题,除个别省市以外,绝大多数都以解答题的形式出现,其中有不少为压轴题.2009年各地考题中不等式恒成立问题的出现也比较频繁,主要特点有:以函数为载体、导数为工具的题占绝大多数;以绝对值不等式为载体的题正在增多;以数列与不等式为载体的题目正在减少,虽然安徽、四川等地仍以数列与不等式为载体,但其难度、技巧性也低于往年.
2 命题走势
新课程的高考命题注重函数思想的能力立意,因此以函数为载体的不等式恒成立问题还将会是今后的主角;含绝对值不等式的恒成立问题可能会增加,新课程卷更有可能出现与绝对值三角不等式、柯西不等式等结合的恒成立问题;以数列为载体的不等式问题将会降低难度.
3 典例剖析
3.1 化归为最值问题求解
求解f(x) 相应地,f(x)≤g(a)恒成立⟺f(x)max≤g(a);f(x)>g(a)恒成立⟺f(x)min>g(a)(或下确界inff(x)≥g(a));f(x)≥g(a)恒成立⟺f(x)min≥g(a). 例1关于x的不等式x2+2bx+1>0当x∈(0,1]时恒成立,求a的取值范围. 分析1求出f(x)=x2+2bx+1在x∈(0,1]上的最小值,则问题转化为不等式f(x)min>0求解. 按函数f(x)=x2+2bx+1=(x+b)2+1-b2的对称轴x=-b与区间(0,1]的位置关系分类如下: (1)当-b≤0,即b≥0时,f(x)min>f(0)=1>0恒成立,此时b≥0; (2)当0<-b≤1,即-1≤b<0时, f(x)min=f(-b)=1-b2>0, 解得 -1 此时 -1 (3)当-b>1,即b<-1时, f(x)min=f(1)=2+2b>0, 解得b>-1,此时没有符合条件的实数. 综上所述,b的取值范围为b>-1. 分析2结合二次函数图像,按判别式符号进行分类. (1)当Δ=4b2-4<0,即-1 x2+2bx+1>0 当x∈(0,1]时恒成立,此时-1 (2)Δ=4b2-4=0,即b=±1.当b=1时,f(x)=(x+1)2>0在x∈(0,1]上恒成立;当b=-1时,f(x)=(x-1)2>0在x∈(0,1]上的最小值为0,不合要求,此时只有b=1. (3)当Δ=4b2-4>0,即b<-1或b>1时,要使f(x)=x2+2bx+1>0在x∈(0,1]上恒成立,结合二次函数图像知,除了f(0)=1>0外,b还要满足 解得b≥0,此时b>1. 综上所述,b的取值范围为b>-1. 评注(1)本题是以一元二次不等式为载体考查不等式恒成立问题的.3个“二次”一脉相承,求解此类问题时要灵活地运用一元二次不等式、二次函数和一元二次方程之间的内在联系,合理地相互转化,以达到解决问题的目的. (2)等价转化为最值问题是求解不等式恒成立问题的基本方法之一,求最值时常要进行分类讨论.“f(x)>0在[a,b]上恒成立”,就是“使[a,b]内的每一个值都能使f(x)>0成立”.因此可以先在[a,b]内取特殊值初步估计出参数的范围,这样有望简化或者避免分类讨论.例如在题目中由f(1)=2b+2>0初步估计得b>-1.这样分析1就可以避免对第3种情况的讨论,简化分类讨论;有时,利用此法还可以避免分类讨论. (2009年湖北省数学高考试题改编) 分析由条件f′(x)=-x2+2bx+c,得 g(x)=|f′(x)|=|-(x-b)2+b2+c|. 只要求出g(x)在[-1,1]的最大值M的最小值. (1)当|b|>1时,函数y=f′(x)的对称轴x=b位于区间[-1,1]之外,此时y=f′(x)在[-1,1]上是单调的,其最值在2个端点处取得.故M=max{g(-1),g(1)},于是 2M≥g(1)+g(-1)= |-1+2b+c|+|-1-2b+c|≥ |(-1+2b+c)-(-1-2b+c)|= 4|b|>4, 即M>2. (2)当|b|≤1时,函数y=f′(x)的对称轴x=b位于区间[-1,1]内,此时 M=max{g(-1),g(1),g(b)}, 于是 4M≥g(-1)+g(1)+2g(b)= |-1-2b+c|+|-1+2b+c|+2|b2+c|≥ |(-1-2b+c)+(-1+2b+c)-2(b2+c)|= |2b2+2|≥2, 解得 评注此题是以含绝对值不等式为载体考查不等式恒成立问题的.求最值时要灵活运用含绝对值不等式||a|-|b||≤|a±b|≤|a|+|b|,例如题中求解时都是为了消去参数c而灵活选取公式.第2种情况的求解:由f′(1)-f′(-1)=4b可分-1≤b≤0与0 f′(1)≤f′(-1)≤f′(b), 所以 g(-1)≤max{g(1),g(b)}, 则M= max{|f′(1)|,|f′(b)|}≥ 当0 分离参数就是通过恒等变形,使参数和主元分别位于不等式的2边,将其转化为本文的第1类问题即等价转化为最值问题求解. (2009年山东省数学高考文科试题改编) 令g′(x)=0,得 评注(1)本题是一个函数单调性问题,此类问题常通过等价转化的方法将其转化为不等式恒成立问题来求解. 由于解题的需要,根据不等式的特征构造一个新的函数,进而转化为求解所构造的函数的相应的最值问题. (2009年辽宁省数学高考理科试题改编) f(x1)-f(x2)+x1-x2>0, 即 f(x1)+x1>f(x2)+x2, 因此构造函数g(x)=f(x)+x,然后证明它在(0,+∞)递增即可. 由1 g′(x)>0, 即g(x)在(0,+∞)上单调增加,从而当x1>x2>0时,有g(x1)>g(x2),即 f(x1)-f(x2)+x1-x2>0, 故 同理,当0 评注本题根据不等式的结构特征构造了一个新的函数,通过求导确定所构造函数的单调性求解.题中没有导数的迹象,可能会导致学生只重视传统方法思考而束手无策,因此高三复习时要注重导数应用的复习. 当不等式(或通过变形后得到的不等式)2边的函数的最值存在,而且不等式2边的函数图形易作时,常画出相应的函数图像,借助函数图像的位置关系确定参数的取值范围. 例5关于x的不等式x2+25+|x3-5x2|≥ax在[1,12]上恒成立,求实数a的取值范围. 图1 图2 由图像可知,当14-a≥4时,y1≥y2恒成立;当a-1≤9时,y3≥y4恒成立.求得a的取值范围为a≤10. 在处理某些不等式恒成立问题时,适当地变更主元,交换主元变量与参数的“地位”,构造新函数求解. 例6设函数f(x)的定义域为R,若对于任意实数m,总有f(m+n)=f(m)·f(n),且当x>0时,0 分析由题设可得,当f(0)=1且x<0时,f(x)>1,f(x)在R上单调递减,所以当x∈[0,+∞)时,f(x)max=f(0)=1. 要使f(x)≤m2-2am+1对所有x∈[0,+∞),a∈[-1,1]恒成立,只要m2-2am+1≥1,即m2-2am≥0在a∈[-1,1]上恒成立. 令g(a)=-2ma+m2,此式为关于a的一次函数,它在a∈[-1,1]上的最值必在闭区间的2个端点处取得,所以m2-2am≥0在a∈[-1,1]上恒成立等价于 解得 m≤-2或m=0或m≥2. 故m的取值范围是m∈(-∞,-2]∪{0}∪[2,+∞). 评注本题涉及到的变量有3个,求解多元变量的不等式恒成立问题,通常可利用逐步固定法.如题中先固定m和a,解决以x为主元的不等式恒成立问题,进而求解以m和a为变量的不等式恒成立问题.不等式m2-2am≥0是关于m的二次不等式,变更主元后,降为以a为主元的一次不等式,从而简化了运算.在一般情况下,函数y=f(m,x)遵循“已知哪个变量的范围,就是这个变量为主元”的原则. 精题集粹 1.在下列函数中,满足“对任意x1,x2∈(0,+∞),当x1 ( ) C.f(x)=exD.f(x)=ln(x+1) 2.设y=f(x)在R上有定义.对于给定的正数K,定义函数 取函数f(x)=2-x-e-x,若对任意的x∈R,恒有fK(x)=f(x),则 ( ) A.K的最大值为2 B.K的最小值为2 C.K的最大值为1 D.K的最小值为1 3.不等式|x+3|-|x-1|≤a2-3a对任意实数x恒成立,则实数a的取值范围为 ( ) A.(-∞,-1]∪(4,+∞) B.(-∞,-2]∪[5,+∞) C.[1,2] D.(-∞,1]∪[2,+∞) 4.当x∈(1,2)时,不等式(x-1)2 ( ) A.[2,+∞) B.(1,2) C.(0,1) D.(1,2] 6.已知f(x)=x3-9x2+24x,若对于任意的m∈[-26,6],恒有f(x)≥x3-mx-11成立,则实数x的取值范围为________. 8.若不等式ax2-|x+1|+2a≥0在R上恒成立,则a的取值范围为________. 9.已知2个函数f(x)=8x2+16x-k,g(x)=2x3+5x2+4x,其中k为实数. (1)对任意x∈[-3,3],都有f(x)≤g(x)成立,求k的取值范围; (2)对任意x1,x2∈[-3,3],都有f(x1)≤g(x2)成立,求k的取值范围. 参考答案 1.A 2.D 3.A 4.D 9.分析(1)问题可转化为h(x)=g(x)-f(x)≥0在x∈[-3,3]上恒成立,求得k≥45. (2)问题转化为在x∈[-3,3]上要满足fmax(x)≤gmin(x),求得k≥141. |f′(x)|min=|f′(1)|=|3-6a-9a2|≤12a. 因为 3-6a-9a2 且 3-6a-9a2≥-12a, 解得 所以


3.2 分离参数







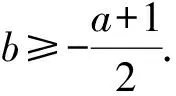


3.3 构造函数


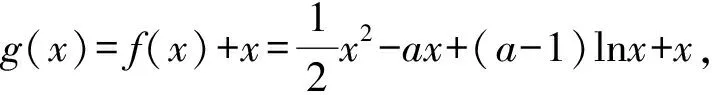
3.4 数形结合



3.5 变更主元