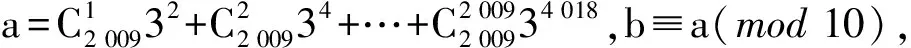2010年数学高考模拟卷(六)
2010-06-08虞金龙
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的4个选项中,只有1项是符合题目要求的.
1.定义集合A*B={x|x∈A,且x∉B}.若A={1,3,5,7},B={2,3,5},则A*B=
( )
A.{1,3} B.{1,5} C.{1,7} D.{2,3}

图1
2.设随机变量ζ服从正态分布N(2,9),若P(ζ>c+1)=P(ζ ( ) A.1 B.2 C.3 D.4 3.图1为一个求20个数的平均数的程序,在横线上应填充的语句为 ( ) A.i>20 B.i<20 C.i>=20 D.i<=20 ( ) 图2 5.图2是一个几何体的三视图,根据图中数据,可得该几何体的表面积是 ( ) A.9π B.10π C.11π D.12π 6.若f(x)是R上的减函数,且f(0)=3,f(3)=-1.设P={x|-1 ( ) A.t≤0B.t≥0C.t≤-3D.t≥-3 图3 7.如图3,用一根铁丝折成一个扇形框架,要求框架所围扇形面积为定值S,则使用铁丝长度最小值为 ( ) ( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法判定其形状 9.银行一年定期的年利率为r,3年定期的年利率为q,银行为吸收长期资金,鼓励储户存3年定期的存款,那么q与r的关系是 ( ) ( ) A.1 012 B.1 286 C.2 009 D.2 010 二、填空题:本大题共7小题,每小题4分,共28分. 12.某高三学生希望报名参加某6所高校中的3所学校的自主招生考试.由于其中2所学校的考试时间相同,因此该学生不能同时报考这2所学校.该学生不同的报考方法种数是________(用数字作答). 13.等差数列{an}的前n项和为Sn,S9=-36,S13=-104.在等比数列{bn}中,b5=a5,b7=a7,则b21的值为________. 图4 图5 三.解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤. (1)求f(x)的单调递增区间; (2)在△ABC中,角A,B,C的对边分别是a,b,c,满足(2a-c)cosB=bcosC,求函数f(A)的取值范围. 图6 (1)现从盒子中任取2张卡片,将卡片上的函数相加得到一个新函数,求所得函数是偶函数的概率; (2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有奇函数卡片则停止抽取,否则继续进行,求抽取次数ζ的分布列和数学期望. (1)求证:平面COD⊥平面AOB; (2)求CD与平面AOB所成角中最大角的正切值. (1)求椭圆C1的方程; (2)求△AkF1F2的面积; (1)设g(x)=x2·f′(x)(x>0),试判断f(x)在区间(0,+∞)上的单调性; (2)若存在唯一实数a∈(m,m+1),使得g(a)=0成立,求正整数m的值; (3)当x>0时,f(x)>n恒成立,求正整数n的最大值. 参考答案 1.C 2.B 3.A 4.A 5.D 6.C 7.D 8.C 9.A 10.C 18.解(1)因为 (2)由(2a-c)cosB=bcosC,得 2sinAcosB-sinCcosB=sinBcosC, 因此 2sinAcosB=sin(B+C)=sinA. 所以 19.解(1)设事件A为“任取2张卡片,将卡片上的函数相加得到的函数是偶函数”,则 (2)ζ可取1,2,3,4. 故ζ的分布列如表1所示. 表1 ζ的分布列 由表1可得 20.解(1)由题意得,CO⊥AO,BO⊥AO,则∠BOC是二面角B-AO-C的平面角.因为二面角B-AO-C是直二面角,所以CO⊥BO.由AO∩BO=O,得CO⊥平面AOB.又CO⊂平面COD,于是平面COD⊥平面AOB. (2)由第(1)小题知,CO⊥平面AOB,于是∠CDO是CD与平面AOB所成的角,且 当OD最小时,∠CDO最大,这时,OD⊥AB,垂足为D,因此 21.解(1)设椭圆C1的半焦距为c,则 解得 于是 b2=a2-c2=36-27=9, (2)点Ak的坐标为(-k,2),则 (1) 由点P在椭圆C上得 代入式(1)并化简得 9y2=112, 因此点M的轨迹方程为 轨迹是2条平行于x轴的线段. 22.(1)证明由 得 g(x)=x-1-ln(x+1)(x>0), 则 因此g(x)在(0,+∞)内单调递增. (2)解因为g(2)=1-ln3<0, g(3)=2(1-ln2)>0, 所以由第(1)小题得,g(x)在(0,+∞)内单调递增,即g(x)=0存在唯一的根a∈(2,3),于是m=2. (3)解由f(x)>n得,n 由g(a)=0,得 a-1-ln(a+1)=0, 即 1+ln(a+1)=a, 于是 f(a)=a+1. 又由a∈(2,3),得 f(a)∈(3,4), 从而n≤3,故正整数n的最大值为3.