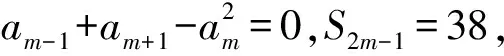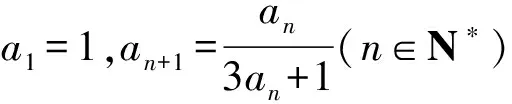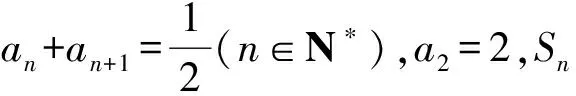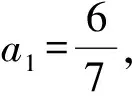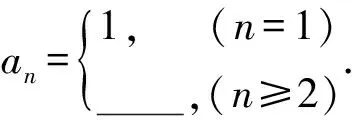数列中的递推方法
2010-06-08知恩中学浙江宁海315600
● (知恩中学 浙江宁海 315600)
1 考查要求
新课程考试大纲没有涉及递推数列,对数列的概念和简单表示法的要求是:了解数列的概念和几种简单的表示方法(列表、图像、通项公式),了解数列是自变量为正整数的一类函数,强调了数列与函数的关系.
2 考点回顾
递推是认识数列的重要手段,递推公式是确定数列的一种方法,要掌握依据数列的递推公式写出数列的前几项及探求数列通项公式的基本方法.数列的通项公式与递推公式从2个不同侧面表达这个数列的特征构造,通项公式与递推公式有时还可以相互转化.给出递推公式,研究数列的通项公式,研究数列不等式是高考的一个热点.这类题目对于考查函数与方程的思想、数形结合的思想、分类与整合思想、化归与转化的思想和特殊与一般的思想方法是理想的素材.纵观近3年的数学高考试题,往往将与递推数列有关的题目放在压轴题.2007年、2008年和2009年数学高考理科试卷涉及递推数列的分别有14份、15份和11份,其中2009年非新课标地区有10份,而新课标地区仅1份,淡化了对递推数列知识的考查.
3 命题走势
(1)填空、解答题均有可能出题,易、中、难均可体现.若为压轴题,则综合性更强.
(2)常规题给出递推关系或以an与Sn为背景间接给出递推关系;热点题将在数列、函数、不等式的交汇处出题,条件或结论是数列递推不等式问题,能力要求高,体现了高考的选拔功能.
(3)新课标地区弱化对递推数列的考查,重视对数列的基本知识与基本方法、等差数列、等比数列的考查.
4 典例剖析
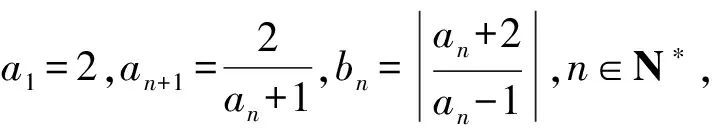
(2009年重庆市数学高考试题)
解由条件得
因为b1=4,所以数列{bn}是首项为4、公比为2的等比数列,于是
bn=4·2n-1=2n+1.
评注本题主要考查等比数列的定义和数列递推公式的灵活应用.
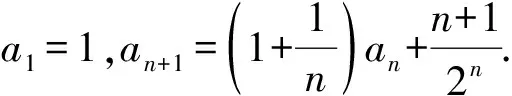

(2)求数列{an}的前n项和Sn.
(2009年全国数学高考试题Ⅰ)
解(1)由已知得
因此
利用累差迭加即可求出数列{bn}的通项公式为
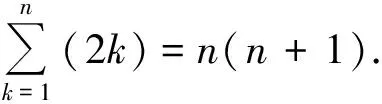

所以
评注2009年全国数学高考理科试题Ⅰ将数列题前置,考查构造新数列和利用错位相减法求前n项和问题,一改往年的将数列结合不等式,利用放缩法作为解题的命题模式,具有让考生和一线教师重视教材和基础知识、基本方法和基本技能,重视两纲的导向作用.也可看出命题人有意识降低难度和求变的良苦用心.
例3在数列{an}与{bn}中,a1=1,b1=4,数列{an}的前n项和Sn满足nSn+1-(n+3)Sn=0,2an+1为bn与bn+1的等比中项,n∈N*.
(1)求a2,b2的值;
(2)求数列{an}与{bn}的通项公式;
(3)设Tn=(-1)a1b1+(-1)a2b2+…+(-1)anbn,n∈N*,证明:|Tn|<2n2,n≥3.
(2008年天津市数学高考试题)
(1)解由题设有a1+a2-4a1=0,a1=1,解得a2=3.又由题设有
解得
b2=9.
(2)解法1由题设nSn+1-(n+3)Sn=0,a1=1,b1=4,及a2=3,b2=9,进一步可得
a3=6,b3=16,a4=10,b4=25,
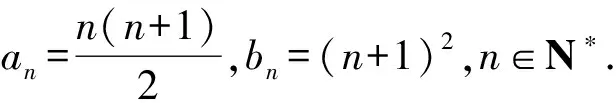
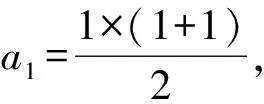
当n≥2时,用数学归纳法证明如下:

②假设当n=k(k≥2)时等式成立,即
则当n=k+1时,由题设知
kSk+1=(k+3)Sk,
(1)
(k-1)Sk=(k+2)Sk-1,
(2)
式(1)-式(2)得
kak+1=(k+2)ak,
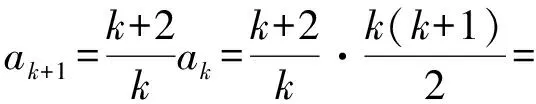
这就是说,当n=k+1时,等式也成立.

再用数学归纳法证明:bn=(n+1)2,n∈N*.
①当n=1时,b1=(1+1)2,等式成立.
②假设当n=k时等式成立,即bk=(k+1)2,则当n=k+1时,
这就是说,当n=k+1时,等式也成立.
根据①和②可知,bn=(n+1)2对任何的n∈N*都成立.
解法2由题设得
nSn+1=(n+3)Sn,
(3)
(n-1)Sn=(n+2)Sn-1,
(4)
式(3)-式(4)得
nan+1=(n+2)an,n≥2.
因此2a3=4a2,3a4=5a3,…,(n-1)an=(n+1)an-1,n≥3,将以上各式左右2端分别相乘得
化简得
此式对n=1,2也成立.
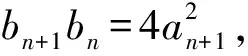
bn+1bn=(n+2)2(n+1)2,
即

xn=1,n≥1,
于是
即
bn=(n+1)2(n≥1).
解法3由题设有nSn+1=(n+3)Sn,n∈N*,因此S2=4S1,2S3=5S2,…,(n-1)Sn=(n+2)Sn-1,n≥2.将以上各式左右两端分别相乘得
1×2×…×(n-1)Sn=4×5×…×(n+2)S1,
(5)
化简得
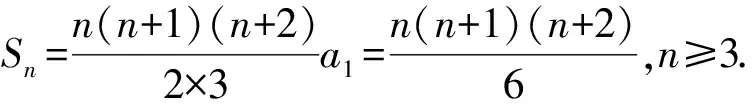
由第(1)小题知,式(5)对n=1,2也成立,所以
上式对n=1时也成立.
以下同解法2,可得bn=(n+1)2.
(3)略.
评注解法1通过数列递推公式和初始条件,先求出该数列的前几项,然后观察这些数的规律,通过发现规律,归纳出通项公式,再用数学归纳法证明对所有正整数都成立.
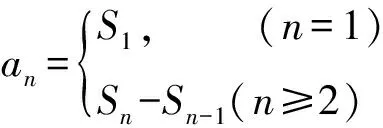
解法3先用“累乘法”求出Sn,然后利用数列的前n项和Sn与数列的通项an的关系求得an.
以上3个解法实质上是数学思想指导的结果,解法1是在特殊与一般思想及有限与无限思想指导下得到的;解法2、解法3是在化归与转化思想指导下得到的.由递推求通项公式只有在数学思想指导下,才能掌握解题规律,积累解题经验,提高思维能力.
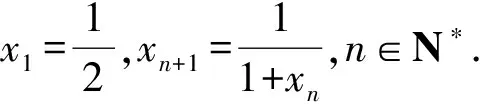
(1)猜想数列{x2n}的单调性,并证明你的结论;
(2009年陕西省数学高考试题)
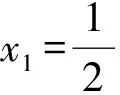
又由x2>x4>x6可猜想:数列{x2n}是递减数列.
下面用数学归纳法证明:
①当n=1时,已证命题成立.
②假设当n=k时命题成立,即x2k>x2k+2,易知x2k>0,则当n=k+1时,

即
x2(k+1)>x2(k+1)+2.
也就是说,当n=k+1时命题也成立.
结合①和②知,命题成立.
(2)证明当n=1时,
结论成立.
当n≥2时,易知0 于是 (1+xn)(1+xn-1)= 评注本题涉及递推数列、数列的单调性、数学归纳法、不等式证明等.思想方法涉及函数与方程、化归与转化、特殊与一般等,用到数学归纳法、代入法、放缩法,对代数运算和推理能力都有较高的能力要求,可以考查学生进入高校继续学习的潜能,体现了高校的选拔需要. 精题集粹 ( ) A.38 B.20 C.10 D.9. ( ) ( ) A.2+lnnB.2+(n-1)lnn C.2+nlnnD.1+n+lnn ( ) 5.已知数列{an}满足:a4n-3=1,a4n-1=0,a2n=an,n∈N*,则a2 009=______;a2 014=______. 6.设{an}是正项数列,其前n项和Sn与通项an满足4Sn=(an-1)(an+3),则数列{an}的通项公式是________. 7.数列{an}满足 9.设数列{an}的前n项和为Sn,已知a1=1,Sn+1=4an+2. (1)设bn=an+1-2an,证明:数列{bn}是等比数列; (2)求数列{an}的通项公式. (1)证明:若a1为奇数,则对一切n≥2,an都是奇数; (2)若对一切n∈N+,都有an+1>an,求a1的取值范围. 参考答案 1.C 2.D 3.A 4.B 9.解(1)记Sn+1=4an+2, (6) 则当n≥2时,有 Sn=4an-1+2. (7) 式(7)-式(6)得 an+1=4an-4an-1, 可化为 an+1-2an=2(an-2an-1). 又因为bn=an+1-2an,所以 bn=2bn-1, 故{bn}是首项b1=3,公比为2的等比数列. (2)由第(1)小题可得 bn=an+1-2an=3·2n-1, 即 从而 故 an=(3n-1)·2n-2. 另一方面,若0 若ak>3,则 根据数学归纳法,0 综上所述,对一切n∈N+都有an+1>an的充要条件是0