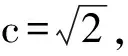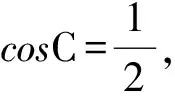解三角形与三角恒等变换
2010-06-08长河高级中学浙江杭州310052
● (长河高级中学 浙江杭州 310052)
1 高考展望
1.1 考点回顾
(1)从近几年的数学高考看,对三角函数的考查,一般是以1~3个客观题和1个解答题的形式出现,以中、低档题为主.解三角形与三角恒等变换是三角函数部分的重要内容,是每年高考必考的一个重要知识点.在涉及三角函数的求值、化简、证明中,都需要运用三角变换,高考中凡是与三角函数有关的问题,也都以恒等变形为研究手段.只有熟悉各个公式在恒等变形中的作用,才能在解决各种问题时合理选择公式、灵活运用公式、提高分析和解决三角问题的能力.在全国各地的高考试题中,主要是直接给出关系式或由向量的运算关系或以三角形等为载体引出,以求值、证明、解不等式或结合不等式、函数最值等来呈现.
(2)尽管对公式的要求有所降低,有“三角函数无难题”之说,但从多年来各类检测和高考的得分情况来看,这部分试题得分率不高,部分学生对概念公式的理解不到位,实际掌握程度低.
(3)对上述内容的考查要注意:
①三角变换问题:主要考查重要公式的灵活运用、变换能力,一般需要运用两角和与差、二倍角公式,尤其是对公式的应用与三角函数性质的综合考查.恒等变换的问题以转化思想为主导,观察差异(或角、或函数名、或运算结构),寻求联系(公式运用或公式的逆用、变形),遵循原则(繁为简、切化弦、异化同、方降次等),实现转化.
②三角函数的应用:以平面向量、三角形、几何或以实际问题等为载体,通过解三角形等来考查三角恒等变形及三角函数性质应用的综合能力.解有关三角形的问题必须熟练掌握正、余弦定理,三角函数以及与三角形面积、周长、内切圆、外接圆等知识,熟知三角形如内角和定理、边角关系等其他隐含着的条件,通过理解这些知识、掌握各知识点间的关系并能够运用这些知识解决一些实际问题.
1.2 命题趋势
三角函数知识是一个传统考点,这部分知识点历久不衰,越考越新,需要引起教师与学生的重点关注.笔者预计在今后的高考中,仍以小而活的选择题、填空题和小型综合题的形式出现;属于容易加中档题,属于三基内容,对学生而言,必须会做而且做对;命题的分值比重在20分左右.若出现大题,则一般放在前三大题,第一道可能性最大,属于得分的权重章节.
三角函数式的恒等变换的知识点有诱导公式、同角的三角函数关系、和差角和倍角公式,其中的倍角公式的几个变形“降次公式”是重中之重.凡考查三角函数的图像性质及解三角形的题往往需要运用三角公式进行化简、求值.注重三角化简的通性通法:从函数名、角、运算这3个方面进行差异分析,常用的技巧有:切割化弦、异角化同角、异名化同名、高次化低次等.
解三角形问题将会以多种形式出现,主要考查正、余弦定理及利用三角公式进行恒等变形的技能与运算能力,以化简、求值或判断三角形形状为主.
新课程改革重视数学的应用,2009年浙江省数学高考把应用题作为填空题来考,2010年的试卷考查实际应用题的方针不会改变,三角函数作为一个重要的数学工具,它的实际应用不可忽视.
2 典例剖析
三角函数解答题多集中在以下几种类型.
2.1 三角函数的变形、化简、求值问题
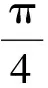
( )
A.y=cos2xB.y=2cos2x
(2009年山东省数学高考理科试题)
点评本题主要考查三角函数图像的变换和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.
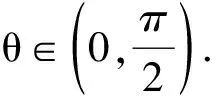
(1)求sinθ和cosθ的值;
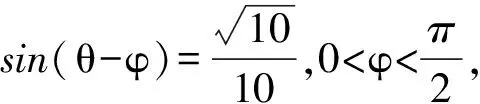
(2009年广东省数学高考理科试题)
解(1)由a与b互相垂直,得
a·b=sinθ-2cosθ=0,
即
sinθ=2cosθ,
代入sin2θ+cos2θ=1得
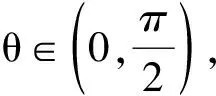
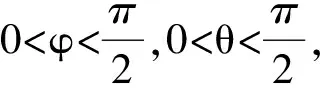
因此
从而 cosφ= cos[θ-(θ-φ)]=
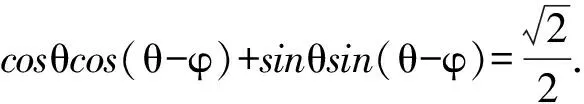
点评(1)本题主要考查简单的向量、三角变换及其计算,而解决三角变形问题的关键是掌握基本变换思想,充分运用和角与差角、倍角与半角的变形公式.
(2)求值是三角函数的基本问题,本题是一道有关条件求值的问题.解决这类问题的关键是寻求条件和欲求结论之间的关系,通常从“角、名、形”这几个方面入手进行分析.本题首先运用向量运算将条件转化为“sinθ=2cosθ”,再寻求与第(1)小题欲求结论之间的联系;第(2)小题还遇到角的整体转换及公式灵活运用的问题,尽管还可以运用直接将条件用公式展开这种比较繁琐的方法.可以发现把握整体、寻求转化是数学解题的一种重要途径.
2.2 涉及解三角形的三角函数问题
例3在△ABC中,内角A,B,C的对边长分别为a,b,c,已知a2-c2=2b,且sinAcosC=3cosAsinC,求b.
(2009年全国数学高考理科试题Ⅰ)
解法1在△ABC中,因为
sinAcosC=3cosAsinC,
所以由正弦定理及余弦定理有
化简并整理得
2(a2-c2)=b2.
又由已知a2-c2=2b,得4b=b2,解得
b=4或b=0(舍去).
解法2由余弦定理得
a2-c2=b2-2bccosA.
因为a2-c2=2b,b≠0,所以
b=2ccosA+2.
(1)
又
sinAcosC=3cosAsinC,
所以
sinAcosC+cosAsinC=4cosAsinC,
即
sin(A+C)=4cosAsinC,
从而
sinB=4cosAsinC.
b=4ccosA,
(2)
由式(1),式(2),解得b=4.
点评(1)事实上此题比较简单,但考生反应不知从何入手.对已知条件a2-c2=2b,左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件sinAcosC=3cosAsinC,过多地关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,找不到突破口而失分.
(2)在解决三角形的有关问题时,主要通过正弦定理和余弦定理进行边角互化,但也要注意一些隐含条件的利用.例如,在三角形中,内角和定理及诱导公式带来的等量关系如“sinA=sin(B+C),…”、三边关系、最大及最小内角范围等等.
(3)近几年高考明显加强对正、余弦定理的考查,并与向量、平面几何、解析几何等知识交汇,在备考中应注意总结,提高自己对问题的分析和解决能力及对知识的灵活运用能力.
2.3 三角函数与平面向量等的交汇问题

(2009年安徽省数学高考理科试题)
解设∠AOC=α,由题意得

图1
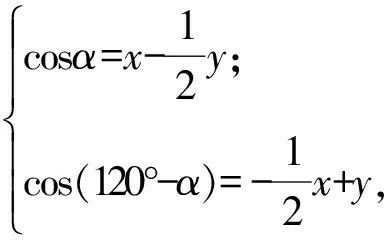
因此x+y=
2[cosα+cos(120°-α)]=
点评(1)本题题型新颖,虽然是一道以向量为背景的填空题,但考生难以得分,主要是多种知识交汇,有函数思想要求:从“点C在以O为圆心的圆弧AB上变动”想到设“∠AOC=α”,并灵活应用平面向量知识和方程思想,同时考查三角恒等变换和三角函数这一“函数”功能求最值.
(2)三角不仅是数学运算的工具,也是重要的函数,是数学许多知识点的交汇中心.在多种知识点交汇处命题,可体现考试公平公正,避免学生不求理解、盲目做题,真正考出考生的解决问题能力.笔者认为将此题设计为解答题更能体现今后的高考导向作用.
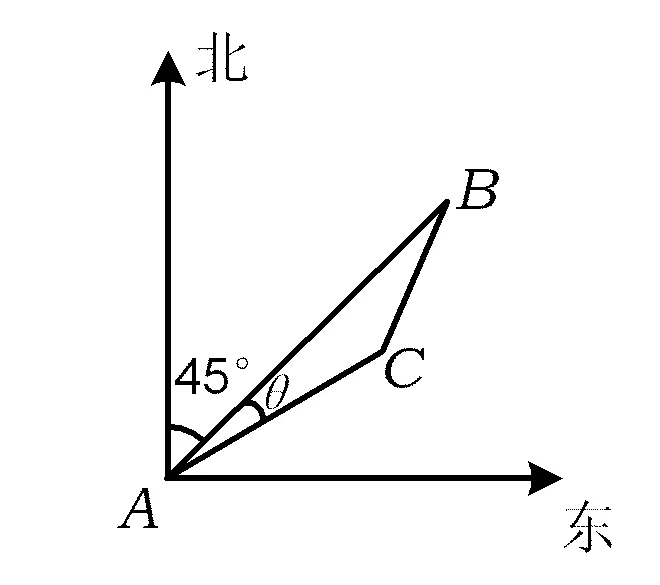
图2
2.4 三角函数的实际应用

(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.
(2008年湖南省数学高考试题)
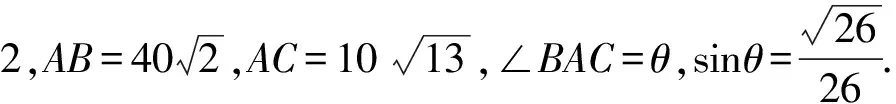
又由余弦定理得
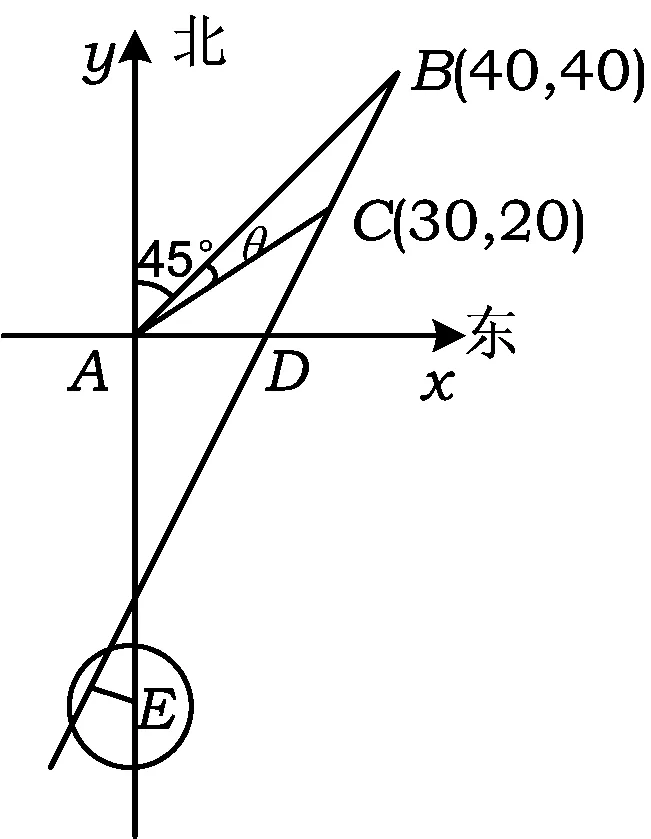
图3
(2)如图3所示,以点A为原点建立平面直角坐标系,设点B,C的坐标分别是B(x1,y1),C(x2,y2),BC与x轴的交点为D.由题设知
x2=ACcos∠CAD=
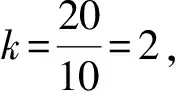
点评(1)本题是一道以海域测量为背景的实际问题,主要考查三角函数、解三角形、解析法等基础知识,考查数学建模、抽象概括和解决实际问题的能力.题目将数学的多个知识网络交汇在一起,对于思维慎密性、书写规范性及运算等方面提出了较高要求.
(2)应用题是新高考的必考内容,数学来源于生活和生产实践,又反过来为生活和生产实践服务.2010年仍将会加大对数学实际应用的考查.
(3)解斜三角形的应用问题通常需根据题意,从实际问题中抽象出一个或几个三角形,通过解这些三角形得出所要求的量,从而得到实际问题的解,其中建立数学模型的方法是我们的归宿,用数学手段来解决实际问题,是学习数学的根本目的.
精题集粹
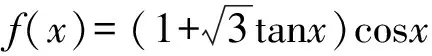
( )
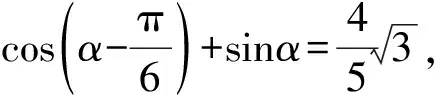
( )
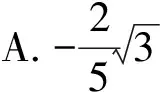

( )
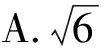
4.有4个关于三角函数的命题:

p2:存在x,y∈R,sin(x-y)=sinx-siny;
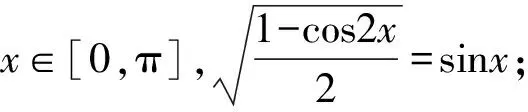
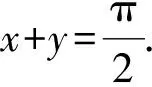
其中假命题的是
( )
A.p1,p4B.p2,p4C.p1,p3D.p2,p4
5.已知函数f(x)=(1+cos2x)sin2x,x∈R,则f(x)是
( )
A.最小正周期为π的奇函数
C.最小正周期为π的偶函数
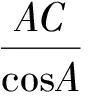
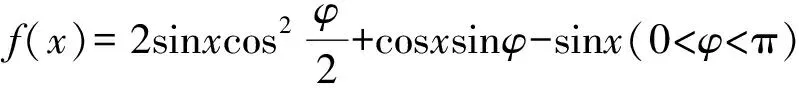
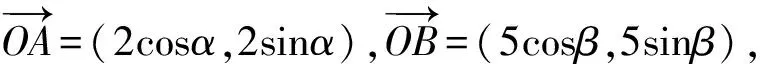

(1)判断△ABC的形状;

11.已知向量m=(sinA,sinB),n=(cosB,cosA),m·n=sin2C,且A,B,C分别为△ABC的3边a,b,c所对的角.
(1)求角C的大小;

参考答案
1.A 2.C 3.D 4.A 5.D
10.解(1)因为
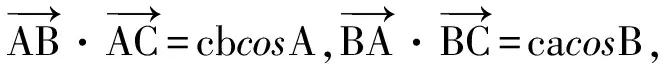

bccosA=accosB,
于是
sinBcosA=sinAcosB,
即
sinAcosB-sinBcosA=0,
从而
sin(A-B)=0.
又-π (2)由第(1)小题知a=b,因此 11.解(1)m·n= sinA·cosB+sinB·cosA= sin(A+B), 对于△ABC,A+B=π-C,0 sin(A+B)=sinC, 即 m·n=sinC. 又因为m·n=sin2C,所以 sin2C=sinC, (2)由sinA,sinC,sinB成等差数列,得 2sinC=sinA+sinB. 由正弦定理得2c=a+b.又已知 即 abcosC=18,a=36. 由余弦定理 c2=a2+b2-2abcosC=(a+b)2-3ab, 即 c2=4c2-3×36, 解得 c=6.