导数应用的题型与高考走势

● (浙江大学附属中学 浙江杭州 310007)

1 考查要求

掌握函数在一点处导数的定义和导数的几何意义，熟记基本导数公式，掌握2个函数四则运算的求导法则和复合函数的求导法则，了解可导函数在某点取得极值的必要条件和充分条件(导数要极值点2侧异号)，能用导数求单调区间、求函数的极值与最值的问题，应用于解决实际问题.

2 考点回顾

导数是研究函数的工具，导数进入新教材之后，给函数问题注入了生机和活力，开辟了许多解题新途径，拓展了高考对函数问题的命题空间.函数与导数问题也是近几年高考的热点问题,在解题中要求考生能以导数为工具，它常与解析几何、不等式、函数等知识交汇，并且明显加大了考试力度，更注重对考生能力的考查.一般有1～2个客观题，1个解答题，分值占20～25分.

3 命题走势

通过对近几年高考中出现的有关导数考题的探索和研究，可以预测2010年高考涉及导数知识的试题大致可分为3个层次：(1)导数的概念和几何意义、求导公式和法则.(2)利用导数研究函数性质及简单应用，包括判断图像、求函数的极值、单调区间，证明函数的增减性等.(3)综合考查，落实在知识的交汇处设计试题，包括以函数为模型运用导数解决的应用问题，将导数内容和不等式、函数的单调性等结合在一起；以导数的几何意义为背景设置导数与解析几何、函数的综合题已成为高考的热点.第(1)、(2)次层次要求以选择题和填空题的形式为主，第(3)层次主要出现在解答题的中档题或压轴题中.

4 典例剖析

(1)掌握函数在一点处的导数的定义,常用求导公式.四则运算求导法则和复合函数求导法则等的灵活运用.

分析在导数定义中，增量Δx的形式是多种多样的，但不论Δx选择哪种形式，Δy也必须选择相对应的形式.利用函数f(x)在x=a处可导的条件，可以将已给定的极限式恒等变形转化为导数定义的结构形式.

(2)利用导数的几何意义求切线问题.

( )

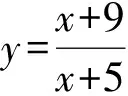
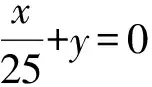
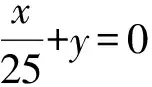
分析“曲线在点P处的切线”只有1条，且P为切点；“曲线过点P处的切线”有2条,P则不一定是切点.注意“曲线在点P处的切线”与“曲线过点P的切线”的区别.

于是y′(x0)=k,即

解得

x0=-3或x0=-15,

因而

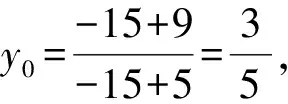
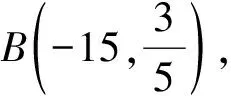
及

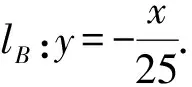
(3)利用导数求函数单调区间、极值和最值,研究函数性质和图像,与函数、不等式综合在一起，解决单调性、参数的范围等问题.单调性问题可转化为含参数的一元二次不等式或高次不等式的问题求解，从而达到考查分类与整合、化归与转化的数学思想.

例3已知函数f(x)=(x2+ax-2a2+3a)ex(x∈R),其中a∈R.

(1)当a=0时，求曲线y=f(x)在点(1,f(1))处的切线的斜率；

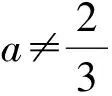
(2009年天津市数学高考理科试题)

分析本题主要考查导数的几何意义、导数的运算、利用导数研究函数的单调性与极值等基础知识，考查运算能力及分类讨论的思想方法.

解(1)当a=0时，

f(x)=x2ex,

则

f′(x)=(x2+2x)ex,

因此f′(1)=3e,所以曲线y=f(x)在点(1，f(1))处的切线的斜率为3e.

(2)f′(x)=[x2+(a+2)x-2a2+4a]ex.

令f′(x)=0，解得

x=-2a或x=a-2.

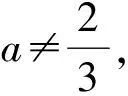
-2a≠a-2.

以下分2种情况进行讨论.

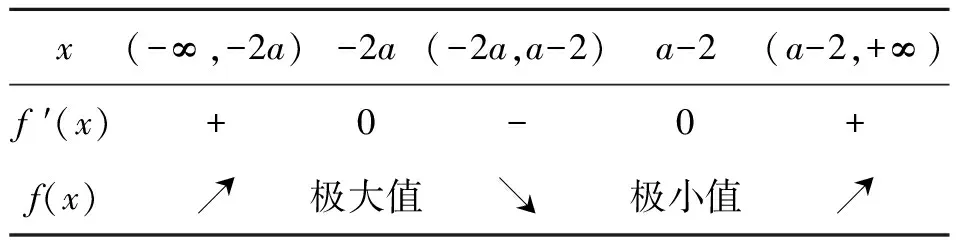
表1 f ′(x),f(x)的变化表

所以f(x)在(-∞,-2a),(a-2,+∞)上是增函数，在(-2a,a-2)上是减函数，函数f(x)在x=-2a处取得极大值f(-2a)，且f(-2a)=3ae-2a;在x=a-2处取得极小值f(a-2),且f(a-2)=(4-3a)ea-2.

表1 f ′(x),f(x)的变化表

所以f(x)在(-∞,a-2),(-2a,+∞)上是增函数，在(a-2,-2a)上是减函数.故函数f(x)在x=a-2处取得极大值f(a-2)，且f(a-2)=(4-3a)ea-2;在x=-2a处取得极小值f(-2a),且f(-2a)=3ae-2a.

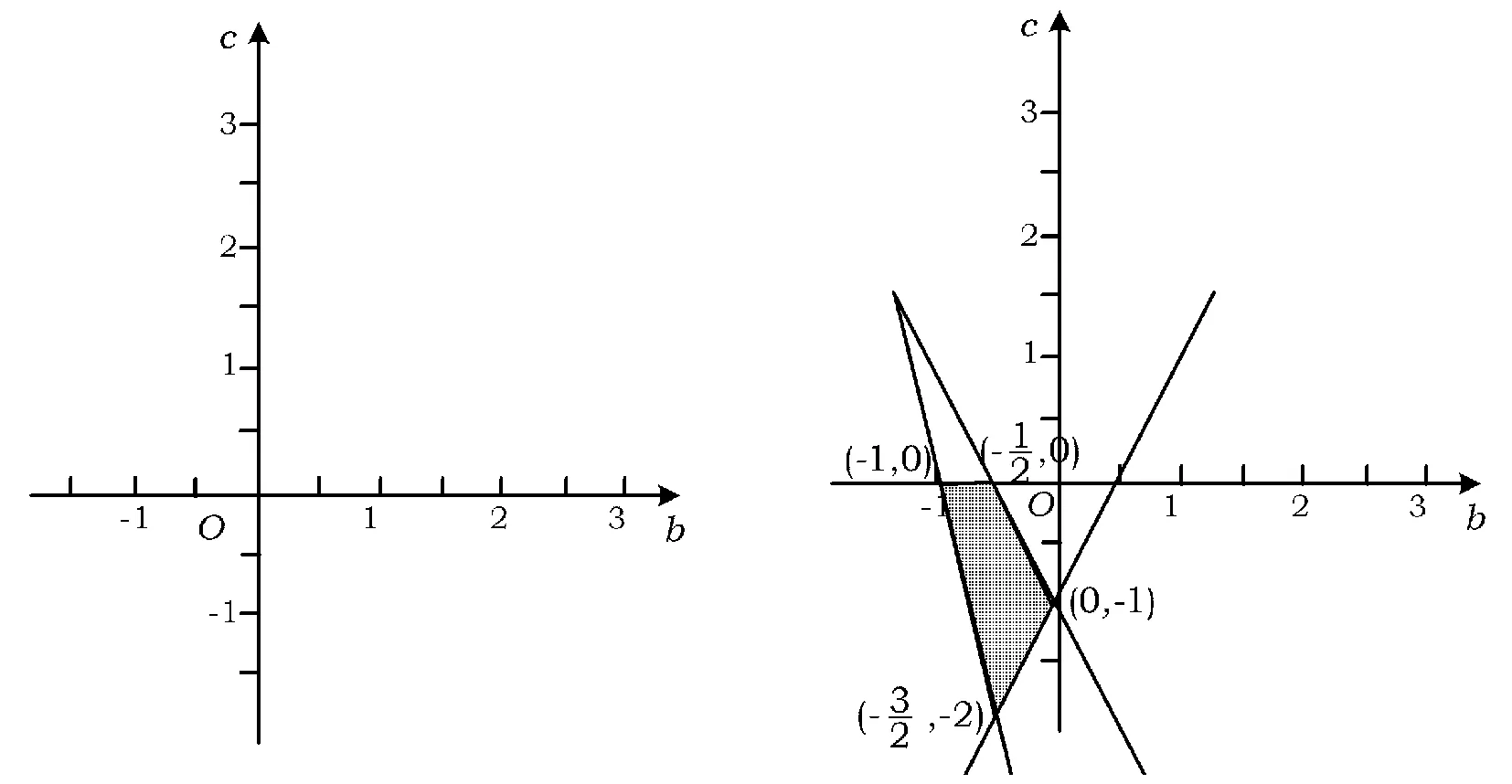
图1 图2

例4设函数f(x)=x3+3bx2+3cx有2个极值点x1,x2，且x1∈[-1,0],x2∈[1,2].

(1)求b,c满足的约束条件，并在如图1所示的坐标平面内，画出满足这些条件的点(b,c)的区域；

(2009年全国数学高考理科试题)

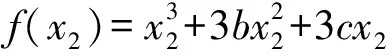
(1)解f′(x)=3x2+6bx+3c.

依题意知，方程f′(x)=0有2个根x1,x2，且x1∈[-1,0],x2∈[1,2].这等价于

f′(-1)≥0,f′(0)≤0,f′(1)≤0,f′(2)≥0,

由此得b,c满足的约束条件为

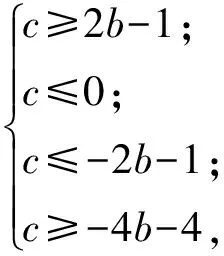
满足这些条件的点(b,c)的区域为图2的阴影部分.

(2)证明由题设知

则

因为x2∈[1,2]，而由第(1)小题知c≤0，所以

又由第(1)小题知c∈[-2,0],因此

(4)以函数为模型运用导数解决实际的应用问题.

在生产、生活等实际问题中，常常需要研究一些成本最低、利润最大、用料最省的问题.我们先把实际情景翻译为数学语言，找出情景中主要的关系，抽象出具体的数学问题，化归为研究目标函数的最大(小)值，从而可利用导数方法简捷求解，此类问题称为优化问题.在解答此类问题时，需要抓住3个基本步骤：①建立函数关系；②求极值点，确定最大(小)值；③回归优化方案．

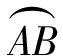
(1)将y表示成x的函数.

(2009年山东省数学高考理科试题)

分析本题主要考查了函数在实际问题中的应用,运用待定系数法求解函数解析式的能力和运用导数研究函数的单调性确定最值问题.

图3

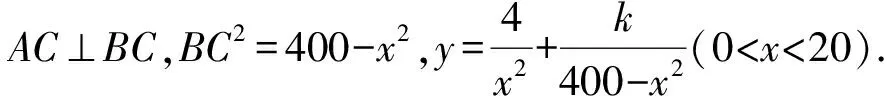
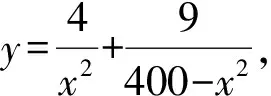
令y′=0,得

18x4=8(400-x2)2,

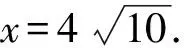
例6某分公司经销某种品牌产品，每件产品的成本为3元，并且每件产品需向总公司交a元(3≤a≤5)的管理费，预计当每件产品的售价为x元(9≤x≤11)时，一年的销售量为(12-x)2万件.

(1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式；

(2)当每件产品的售价为多少元时，分公司一年的利润L最大，并求出L的最大值Q(a).

(2007年福建省数学高考理科试题)

分析本题考查函数、导数及其应用等知识，考查运用数学知识分析和解决实际问题的能力.解决这类问题的关键在于从实际问题中建立函数模型，然后利用导数来求最值,特别要注意确定其定义域.

解(1)分公司一年的利润L(万元)与售价x的函数关系式为

L=(x-3-a)(12-x)2,x∈[9,11].

(2)由第(1)小题得

L′(x)=(12-x)2-2(x-3-a)(12-x)=

(12-x)(18+2a-3x).

令L′=0,得

因为3≤a≤5，所以

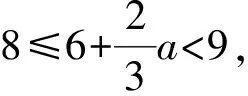
Lmax=L(9)=(9-3-a)(12-9)2=9(6-a)．

故